Материал из Викиконспекты
| Определение: |
Детерминированным автоматом с магазинной памятью (англ. deterministic pushdown automaton) называется автомат с магазинной памятью, для которого выполнены следующие условия:
- [math]\mathcal8 q \in Q, a \in \Sigma \cup \{ \varepsilon \}, X \in \Gamma \Rightarrow \delta(q, a, X)[/math] имеет не более одного элемента — [math] \delta : Q \times \Sigma \cup \{\varepsilon\} \times \Gamma \rightarrow Q \times \Gamma^*[/math].
- Если [math]\delta (q,a,X)[/math] непусто для некоторого [math]a \in \Sigma[/math], то [math]\delta (q,\varepsilon,X)[/math] должно быть пустым.
|
Построим для языка:
- [math] S \rightarrow 1H [/math]
- [math] H \rightarrow 0F [/math]
- [math] H \rightarrow \varepsilon [/math]
- [math] F \rightarrow 0F [/math]
- [math] F \rightarrow 1F [/math]
- [math] F \rightarrow \varepsilon [/math]
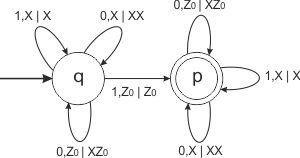
автомат [math]A=(\{0,1\}, \{Z_0,X\}, \{q,p\}, q, \{p\}, Z_0, \delta)[/math] с функией перехода [math]\delta[/math]:
- [math]\delta(q,0,Z_0)=(q,XZ_0)[/math]
- [math]\delta(q,0,X) =(q,XX)[/math]
- [math]\delta(q,1,X) =(q,X)[/math]
- [math]\delta(q,1,Z_0)=(p,Z_0)[/math]
- [math]\delta(p,0,Z_0)=(p,XZ_0)[/math]
- [math]\delta(p,0,X) =(p,XX)[/math]
- [math]\delta(p,1,X) =(p,X)[/math]
См. такжеИсточники информации
- Хопкрофт Д., Мотвани Р., Ульман Д. — Введение в теорию автоматов, языков и вычислений, 2-е изд. : Пер. с англ. — Москва, Издательский дом «Вильямс», 2008. — 528с. : ISBN 978-5-8459-1347-0 (рус.)
