Детерминированные автоматы с магазинной памятью, допуск по пустому стеку — различия между версиями
Kirillova (обсуждение | вклад) |
Kirillova (обсуждение | вклад) (изменены рисунки) |
||
| Строка 13: | Строка 13: | ||
<tex>\Rightarrow</tex><br> | <tex>\Rightarrow</tex><br> | ||
Допустим, что <tex>L</tex> не беспрефиксный. Тогда <tex>\exists \omega_1, \omega_2 \in L : \omega_2 = \omega_1 \alpha</tex>. Попробуем допустить слово <tex>\omega_2</tex>. Тогда автомат остановится сразу после префикса <tex>\omega_1</tex>, т.к. <tex>\omega_1 \in L</tex>. Стек будет пустой, однако до конца слова <tex>\omega_2</tex> мы не дойдем, поэтому оно не допустится, хотя содержится в <tex>L</tex>. Получили противоречие, значит <tex>L</tex> {{---}} беспрефиксный.<br> | Допустим, что <tex>L</tex> не беспрефиксный. Тогда <tex>\exists \omega_1, \omega_2 \in L : \omega_2 = \omega_1 \alpha</tex>. Попробуем допустить слово <tex>\omega_2</tex>. Тогда автомат остановится сразу после префикса <tex>\omega_1</tex>, т.к. <tex>\omega_1 \in L</tex>. Стек будет пустой, однако до конца слова <tex>\omega_2</tex> мы не дойдем, поэтому оно не допустится, хотя содержится в <tex>L</tex>. Получили противоречие, значит <tex>L</tex> {{---}} беспрефиксный.<br> | ||
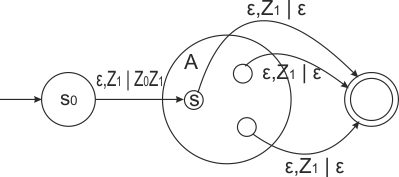
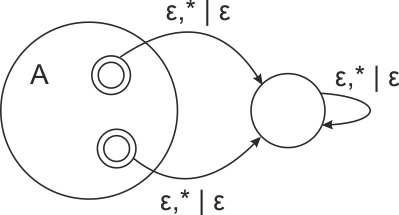
| − | Построим по заданному ДМП-автомату с допуском по пустому стеку ДМП с допуском по допускающему состоянию.<br> | + | Построим по заданному ДМП-автомату с допуском по пустому стеку ДМП с допуском по допускающему состоянию.<br> <br> |
[[Файл:ДМП1.png]]<br> | [[Файл:ДМП1.png]]<br> | ||
<tex>\Leftarrow</tex><br> | <tex>\Leftarrow</tex><br> | ||
Версия 21:31, 2 декабря 2011
| Определение: |
| Определим детерминированный автомат с магазинной памятью, допускающий по пустому стеку, как детерминированный автомат с магазинной памятью, у которого нет множества допускающих состояний. Автомат заканчивает свою работу как только стек становится пустым. |
Определим для него множество допускающих слов , где — произвольное состояние.
| Определение: |
| Язык называется беспрефиксным, если для любой пары слов из этого языка ни одно из этих слов не является префиксом другого. |