Несовпадение класса языков, распознаваемых ДМП автоматами и произвольными МП автоматами — различия между версиями
Leugenea (обсуждение | вклад) (Некоторое пояснение) |
(добавлено доказательство не-КС языка) |
||
| Строка 4: | Строка 4: | ||
|statement=Классы языков, задаваемых МП-автоматами и ДМП-автоматами с допуском по допускающему состоянию не совпадают. | |statement=Классы языков, задаваемых МП-автоматами и ДМП-автоматами с допуском по допускающему состоянию не совпадают. | ||
|proof=[[Файл:pda_1.png|320px|thumb|right|Автомат <tex>M</tex>]] | |proof=[[Файл:pda_1.png|320px|thumb|right|Автомат <tex>M</tex>]] | ||
| − | Рассмотрим язык <tex>L=\left\{0^n1^n \cup 0^n1^{2n}\right\}</tex>. | + | Рассмотрим язык <tex>L=\left\{0^n1^n\right\} \cup \left\{0^n1^{2n}\right\}</tex>. |
Очевидно, что язык <tex>L</tex> является контекстно-свободным. Пусть существует ДМП-автомат с допуском по допускающему состоянию <tex>M</tex>, распознающий его. | Очевидно, что язык <tex>L</tex> является контекстно-свободным. Пусть существует ДМП-автомат с допуском по допускающему состоянию <tex>M</tex>, распознающий его. | ||
| − | В силу детерминированности автомата <tex>(s, z_0, 0^n1^{2n})\vdash^*(q_1, \gamma_1, 1^n)\vdash^*(q_2, \gamma_2, \varepsilon)</tex>, причём <tex>q_1, q_2 \in T</tex>. Рассмотрим также язык <tex>L'=\left\{0^n1^n2^n\right\}</tex>, | + | В силу детерминированности автомата <tex>(s, z_0, 0^n1^{2n})\vdash^*(q_1, \gamma_1, 1^n)\vdash^*(q_2, \gamma_2, \varepsilon)</tex>, причём <tex>q_1, q_2 \in T</tex>. Рассмотрим также язык <tex>L'=\left\{0^n1^n2^n\right\}</tex>. |
| + | |||
| + | Докажем, что язык <tex>L' \cup L = \left\{0^{n}1^{n}2^{n}\right\} \cup \left\{0^n1^n\right\} \cup \left\{0^n1^{2n}\right\}</tex> не является контекстно-свободным. Для фиксированного <tex>n</tex> рассмотрим слово <tex>\omega=0^n 1^n 2^n</tex>. Пусть <tex>\omega</tex> разбили на <tex>u, v, x, y, z</tex> произвольным образом. Так как <tex>|vxy|\leqslant n</tex>, то в слове не содержится либо ни одного символа <tex>0</tex>, либо ни одного символа <tex>2</tex>. Для любого такого разбиения выбираем <tex>k=2</tex> и получаем, что количество символов <tex>1</tex> изменилось, а количество либо <tex>0</tex>, либо <tex>2</tex> осталось тем же. Очевидно, что такое слово не принадлежит рассмотренному языку. Значит, язык <tex>L' \cup L</tex> не является контекстно-свободным по лемме о разрастании для КС-грамматик. | ||
| + | |||
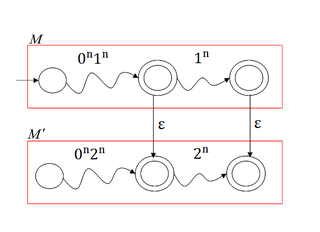
| + | Построим на основе <tex>M</tex> недетерминированный МП-автомат, распознающий <tex>L' \cup L</tex>. Для начала построим по автомату <tex>M</tex> автомат <tex>M'</tex>, заменив все вхождения символа <tex>1</tex> на символ <tex>2</tex>. Далее объединим автоматы <tex>M</tex> и <tex>M'</tex> в автомат <tex>M''</tex>, соединив допускающие состояния <tex>\varepsilon</tex>-переходами (как показано на картинке). | ||
Автомат <tex>M''</tex> является недетерминированным МП-автоматом, и принимает не контекстно-свободный язык <tex>L' \cup L</tex>. | Автомат <tex>M''</tex> является недетерминированным МП-автоматом, и принимает не контекстно-свободный язык <tex>L' \cup L</tex>. | ||
Полученное противоречие доказывает, что нет ДМП-автомата с допуском по допускающему состоянию, распознающего язык <tex>L</tex>. Но из того, что <tex>L</tex> — контекстно-свободный следует, что есть недетерминированный МП-автомат, распознающий его. | Полученное противоречие доказывает, что нет ДМП-автомата с допуском по допускающему состоянию, распознающего язык <tex>L</tex>. Но из того, что <tex>L</tex> — контекстно-свободный следует, что есть недетерминированный МП-автомат, распознающий его. | ||
}} | }} | ||
[[Файл:pda_2.png|320px|thumb|right|Автомат <tex>M''</tex>]] | [[Файл:pda_2.png|320px|thumb|right|Автомат <tex>M''</tex>]] | ||
Версия 01:35, 24 января 2012
В отличие от конечных автоматов, для МП-автоматов недетерминизм является существенным. ДМП-автоматы распознают не все языки, распознаваемые МП-автоматами или КС-грамматиками.
| Теорема: |
Классы языков, задаваемых МП-автоматами и ДМП-автоматами с допуском по допускающему состоянию не совпадают. |
| Доказательство: |
|
Рассмотрим язык . Очевидно, что язык является контекстно-свободным. Пусть существует ДМП-автомат с допуском по допускающему состоянию , распознающий его. В силу детерминированности автомата , причём . Рассмотрим также язык . Докажем, что язык не является контекстно-свободным. Для фиксированного рассмотрим слово . Пусть разбили на произвольным образом. Так как , то в слове не содержится либо ни одного символа , либо ни одного символа . Для любого такого разбиения выбираем и получаем, что количество символов изменилось, а количество либо , либо осталось тем же. Очевидно, что такое слово не принадлежит рассмотренному языку. Значит, язык не является контекстно-свободным по лемме о разрастании для КС-грамматик. Построим на основе недетерминированный МП-автомат, распознающий . Для начала построим по автомату автомат , заменив все вхождения символа на символ . Далее объединим автоматы и в автомат , соединив допускающие состояния -переходами (как показано на картинке). Автомат является недетерминированным МП-автоматом, и принимает не контекстно-свободный язык . Полученное противоречие доказывает, что нет ДМП-автомата с допуском по допускающему состоянию, распознающего язык . Но из того, что — контекстно-свободный следует, что есть недетерминированный МП-автомат, распознающий его. |