Сведение задачи RMQ к задаче LCA — различия между версиями
м |
|||
| Строка 4: | Строка 4: | ||
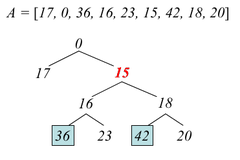
[[Файл:Wiki.PNG|thumb|right|300x160px|Пример построенного дерева для массива А]] | [[Файл:Wiki.PNG|thumb|right|300x160px|Пример построенного дерева для массива А]] | ||
Декартово дерево (англ. ''сartesian tree'') на массиве <tex>A[1..N]</tex> {{---}} это бинарное дерево, рекурсивно определенное следующим образом: | Декартово дерево (англ. ''сartesian tree'') на массиве <tex>A[1..N]</tex> {{---}} это бинарное дерево, рекурсивно определенное следующим образом: | ||
| − | * Корнем дерева является минимальное значение в массиве <tex>A</tex>, скажем <tex>A[i]</tex>. | + | * Корнем дерева является минимальное значение в массиве <tex>A</tex>, скажем <tex>A[i]</tex>. Если минимальных значений несколько, можно взять любое. |
* Левым поддеревом является декартово дерево на массиве <tex>A[1..i-1]</tex>. | * Левым поддеревом является декартово дерево на массиве <tex>A[1..i-1]</tex>. | ||
* Правым поддеревом является декартово дерево на массиве <tex>A[i+1..N]</tex>. | * Правым поддеревом является декартово дерево на массиве <tex>A[i+1..N]</tex>. | ||
Версия 15:53, 8 апреля 2012
Постановка задачи RMQ
Дан массив . Поступают запросы вида , на каждый запрос требуется найти минимум в массиве , начиная с позиции и заканчивая позицией .
Алгоритм
Декартово дерево (англ. сartesian tree) на массиве — это бинарное дерево, рекурсивно определенное следующим образом:
- Корнем дерева является минимальное значение в массиве , скажем . Если минимальных значений несколько, можно взять любое.
- Левым поддеревом является декартово дерево на массиве .
- Правым поддеревом является декартово дерево на массиве .
Построим декартово дерево на массиве . Тогда = .
Доказательство
Мы знаем что:
- Любая вершина дерева всегда имеет меньшее значение, чем её дети. Тогда любой предок или меньше их самих.
- ближайший к корню и по п.1 имеет наименьшее значение в своем поддереве. По построению, это поддерево содержит в частности подмассив и находится между и . То есть является
Сложность
Построение дерева наивным алгоритмом . Существует алгоритм построения за .
Препроцессинг для — и ответ на запрос . В итоге получили {построение , запрос }.