|
|
| Строка 36: |
Строка 36: |
| | | | |
| | == Нахождение реберной связности == | | == Нахождение реберной связности == |
| − | Для нахождения реберной связности воспользуемся [[Теорема Менгера, альтернативное доказательство|следующей теоремой:]]
| |
| − | {{Теорема
| |
| − | |about=
| |
| − | Теорема Менгера для <tex>k</tex>-реберной связности
| |
| − | |statement=
| |
| − | Пусть <tex>G</tex> - конечный, неориентированный граф, <tex>\lambda(G) = k</tex> <tex>\Leftrightarrow</tex> для всех пар вершин <tex>x, y \in G</tex> существует <tex>k</tex> реберно непересекающихся путей из <tex>x</tex> в <tex>y</tex>.
| |
| − | }}
| |
| − | Алгоритм следует непосредственно из теоремы. Нужно перебрать все пары вершин <tex>s</tex> и <tex>t</tex>, найти количество непересекающихся путей из <tex>s</tex> в <tex>t</tex> и выбрать минимум.
| |
| − |
| |
| − | Для нахождения количества непересекающихся путей из <tex>s</tex> в <tex>t</tex> воспользуемся алгоритмом нахождения максимального потока. Сопоставим каждому ребру пропускную способность, равную <tex>1</tex> и найдем максимальный поток.
| |
| − | Он и будет равен количеству путей. Действительно, если провести декомпозицию потока, то получим набор реберно непересекающихся путей из <tex>s</tex> в <tex>t</tex>, по которым поток неотрицателен и равен <tex>1</tex> (т.к. пропускная способность всех ребер равна <tex>1</tex>). А значит, если поток равен <tex>flow</tex>, то и количество путей равно <tex>flow</tex>.
| |
| − |
| |
| − | ''' Псевдокод алгоритма '''
| |
| − | ans = INF
| |
| − | for <tex>s \in V:</tex>
| |
| − | for <tex>t \in V:</tex>
| |
| − | flow = find_flow(s, t)
| |
| − | ans = min(ans, flow)
| |
| − |
| |
| − | '''Оценка работы'''
| |
| − |
| |
| − | Время работы равно <tex>V^2 \times O(find\_flow)</tex>. При использовании [[Алоритм Эдмондса-Карпа|алгоритма Эдмондса-Карпа]] время равно <tex>V^2 \times O(V E^2)</tex> или <tex>O(V^3 E^2)</tex>
| |
| − |
| |
| − | == Нахождение вершинной связности ==
| |
| − | Нахождение вершинной связности сводится к задаче нахождения реберной связности следующим образом.
| |
| − |
| |
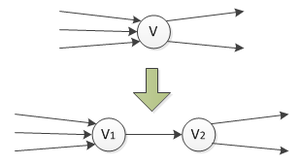
| − | Разобьем каждую вершину <tex>v</tex> графа на две вершины <tex>v_1</tex> и <tex>v_2</tex>. Все ребра, которые входили в <tex>v</tex> будут входить в <tex>v_1</tex>. Все ребра, которые выходили из <tex>v</tex> будут выходить из <tex>v_2</tex>. Так же добавим ребро <tex>(v_1, v_2)</tex>.
| |
| − |
| |
| − | [[Файл:Vertex-2vertex.png|300px|left|thumb|Иллюстрация]]
| |
| − | <br clear="all"/>
| |
| − | В новом графе запустим алгоритм нахождения реберной связности.
| |
| − | == Нахождение реберной связности. ver 2.0 ==
| |
| | В статье про [[K-связность]] было сформулировано следующее утверждение: | | В статье про [[K-связность]] было сформулировано следующее утверждение: |
| | {{Утверждение | | {{Утверждение |
| Строка 96: |
Строка 64: |
| | Время работы равно <tex>V^2 \times O(find\_flow)</tex>. При использовании [[Алоритм Эдмондса-Карпа|алгоритма Эдмондса-Карпа]] время равно <tex>V^2 \times O(V E^2)</tex> или <tex>O(V^3 E^2)</tex> | | Время работы равно <tex>V^2 \times O(find\_flow)</tex>. При использовании [[Алоритм Эдмондса-Карпа|алгоритма Эдмондса-Карпа]] время равно <tex>V^2 \times O(V E^2)</tex> или <tex>O(V^3 E^2)</tex> |
| | | | |
| − | == Нахождение вершинной связности. ver 2.0 == | + | == Нахождение вершинной связности == |
| | Используя аналогичные утверждения и определения для вершинной связности придем к такому же алгоритму с тем отличием, что понадобится искать вершинно-непересекающиеся пути. | | Используя аналогичные утверждения и определения для вершинной связности придем к такому же алгоритму с тем отличием, что понадобится искать вершинно-непересекающиеся пути. |
| | Искать их можно тем же способом, если сопоставить каждой вершине пропускную способность, равную <tex>1</tex>. | | Искать их можно тем же способом, если сопоставить каждой вершине пропускную способность, равную <tex>1</tex>. |
Версия 15:18, 29 декабря 2012
Определения
| Определение: |
| Вершинной связностью [math]\varkappa[/math] графа [math]G[/math] называется наименьшее число вершин, удаление которых приводит к несвязному или тривиальному графу. |
| Определение: |
| Реберной связностью [math]\lambda[/math] графа [math]G[/math] называется наименьшее количество ребер, удаление которых приводит к несвязному или тривиальному графу. |
Связь между вершинной, реберной связностью и минимальной степенью вершины
Пускай минимальная степень вершины графа [math]G[/math] обозначается буквой [math]\delta[/math]. Тогда:
| Теорема: |
Для любого графа [math]G[/math] справедливо следующее неравенство: [math]\varkappa \le\lambda \le \delta [/math] |
| Доказательство: |
| [math]\triangleright[/math] |
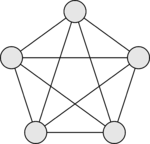 Полный граф. [math] \lambda = \delta = \varkappa = 4[/math]- Проверим второе неравенство. Если в графе [math]G[/math] нет ребер, то [math] \lambda = 0 [/math]. Если ребра есть, то несвязный граф получаем из данного, удаляя все ребра, инцидентные вершине с наименьшей степенью. В любом случае [math] \lambda \le \delta [/math].
- Чтобы проверить первое неравенство нужно рассмотреть несколько случаев.
- Если [math]G[/math] - несвязный или тривиальный граф, то [math] \varkappa = \lambda = 0 [/math].
- Если [math]G[/math] связен и имеет мост [math]x[/math], то [math]\lambda = 1 [/math]. В последнем случае [math] \varkappa = 1 [/math], поскольку или граф [math]G[/math] имеет точку сочленения, инцидентную ребру [math]x[/math], или же [math]G=K_2[/math].
- Наконец, предположим, что граф [math]G[/math] содержит множество из [math] \lambda \ge 2 [/math] ребер, удаление которых делает его несвязным. Ясно, что удаляя [math]\lambda - 1 [/math] ребер из этого множества получаем граф, имеющий мост [math]x = uv[/math]. Для каждого из этих [math]\lambda - 1 [/math] ребер выберем какую-либо инцидентную с ним вершину отличную от [math]u[/math] и [math]v[/math]. Удаление выбранных вершин приводит к удалению [math]\lambda - 1 [/math] (а возможно, и большего числа) ребер. Если получаемый после такого удаления граф не связен, то [math]\varkappa \lt \lambda[/math]; если же он связен, то в нем есть мост [math]x[/math], и поэтому удаление вершины [math]u[/math] или [math]v[/math] приводит либо к несвязному, либо к тривиальному графу. В любом случае [math] \varkappa \le \lambda[/math].
|
| [math]\triangleleft[/math] |
| Теорема: |
Для любых натуральных чисел [math]a, b, c[/math], таких что [math]a \le b \le c[/math], существует граф [math]G[/math], у которого [math]\varkappa = a, \lambda = b[/math] и [math]\delta = c [/math] |
| Доказательство: |
| [math]\triangleright[/math] |
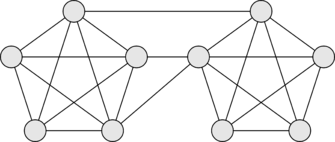 Граф, в котором [math] \delta = 4[/math], [math]\lambda = 3[/math], [math]\varkappa = 2[/math]. Рассмотрим граф [math]G[/math], являющийся объединением двух полных графов [math]G_1[/math] и [math]G_2[/math], содержащих [math]c + 1[/math] вершину. Отметим [math]b[/math] вершин, принадлежащих подграфу [math]G_1[/math] и [math]a[/math] вершин, принадлежащих подграфу [math]G_2[/math]. Добавим в граф [math]G[/math] [math]b[/math] ребер так, чтобы каждое ребро было инцидентно помеченной вершине, лежащей в подграфе [math]G_1[/math] и помеченной вершине, лежащей в подграфе [math]G_2[/math], причем не осталось ни одной помеченной вершины, у которой не появилось хотя бы одно новое ребро, инцидентное ей.
Тогда:
- Поскольку [math]b \le c[/math], то было как минимум две непомеченные вершины, поэтому [math] \delta = c[/math], так как минимальные степени вершин графов [math]G_1[/math] и [math]G_2[/math] были равны [math]c[/math], а степени их вершин не уменьшались.
- Заметим, что между двумя вершинами графа [math]G[/math] существует не меньше [math]a[/math] вершинно-непересекающихся простых цепей, следовательно по теореме Менгера [math]\varkappa \ge a[/math]. Однако если удалить из графа [math]G[/math] помеченные вершины его подграфа [math]G_2[/math], то граф [math]G[/math] потеряет связность. Значит, [math]\varkappa = a[/math].
- Аналогично рассуждению пункта 2, легко убедится, что [math]\lambda = b[/math].
|
| [math]\triangleleft[/math] |
Нахождение реберной связности
В статье про K-связность было сформулировано следующее утверждение:
| Утверждение: |
Граф [math] G [/math] является реберно [math] l [/math] - связным [math]\Leftrightarrow [/math] любая пара его вершин соединена по крайней мере [math] l [/math] - реберно непересекающимися путями. |
Там же было дано определение реберной связности через [math] l [/math]-связность:
| Определение: |
| Реберной связностью графа называется [math] \lambda(G) = \max \{ l | G [/math] реберно [math] l [/math] - связен [math] \} [/math], для тривиального графа считаем [math] \lambda (K_1) = 0 [/math]. |
Для нахождения реберной связности нужно перебрать все пары вершин [math]s[/math] и [math]t[/math], найти количество непересекающихся путей из [math]s[/math] в [math]t[/math] и выбрать минимум.
Пусть он равен [math]l[/math]. По утверждению, граф является [math]l[/math] - связным, причем такое [math]l[/math] - максимально (ведь мы явно нашли количество путей). А значит, по определению, реберная связность равна [math]l[/math].
Для нахождения количества непересекающихся путей из [math]s[/math] в [math]t[/math] воспользуемся алгоритмом нахождения максимального потока. Сопоставим каждому ребру пропускную способность, равную [math]1[/math] и найдем максимальный поток.
Он и будет равен количеству путей. Действительно, если провести декомпозицию потока, то получим набор реберно непересекающихся путей из [math]s[/math] в [math]t[/math], по которым поток неотрицателен и равен [math]1[/math] (т.к. пропускная способность всех ребер равна [math]1[/math]). А значит, если поток равен [math]flow[/math], то и количество путей равно [math]flow[/math].
Псевдокод алгоритма
ans = INF
for [math]s \in V:[/math]
for [math]t \in V:[/math]
flow = find_flow(s, t)
ans = min(ans, flow)
Оценка работы
Время работы равно [math]V^2 \times O(find\_flow)[/math]. При использовании алгоритма Эдмондса-Карпа время равно [math]V^2 \times O(V E^2)[/math] или [math]O(V^3 E^2)[/math]
Нахождение вершинной связности
Используя аналогичные утверждения и определения для вершинной связности придем к такому же алгоритму с тем отличием, что понадобится искать вершинно-непересекающиеся пути.
Искать их можно тем же способом, если сопоставить каждой вершине пропускную способность, равную [math]1[/math].
Для этого воспользуемся известным трюком:
Разобьем каждую вершину [math]v[/math] графа на две вершины [math]v_1[/math] и [math]v_2[/math]. Все ребра, которые входили в [math]v[/math] будут входить в [math]v_1[/math]. Все ребра, которые выходили из [math]v[/math] будут выходить из [math]v_2[/math]. Так же добавим ребро [math](v_1, v_2)[/math].
После этого для нахождения количества вершинно непересекающихся путей в исходном графе будем искать количество реберно непересекающихся в новом графе.
Тем самым сведя задачу к нахождению реберной связности.
Литература
- Харари Ф. Теория графов: Пер. с англ. / Предисл. В. П. Козырева; Под ред. Г.П.Гаврилова. Изд. 4-е. — М.: Книжный дом "ЛИБРОКОМ", 2009. — 60 с.