Материал из Викиконспекты
Теорема Менгера представляет собой группу теорем, связывающих такие понятия на графах как [math]k[/math]-связность и количество непересекающихся путей относительно двух выделенных вершин. Возникают различные варианты очень похожих друг на друга по формулировке теорем в зависимости от того, рассматриваем ли мы ситуацию в ориентированном или неориентированном графе, и подразумеваем ли реберную [math]k[/math]-связность и реберно непересекающиеся пути или же вершинную [math]k[/math]-связность и вершинно непересекающиеся пути.
Для доказательства мы будем пользоваться развитой раннее теорией потоков. Кроме базовых определений нам потребуется понятие остаточной сети (иначе — дополнительной сети), а также теорема Форда-Фалкерсона.
Кроме того, потребуется лемма о целочисленности потока, которую сейчас и докажем:
| Лемма (о целочисленности потока): |
Если пропускные способности всех ребер целочисленные (сеть целочислена), то существует максимальный поток, целочисленный на каждом ребре. |
| Доказательство: |
| [math]\triangleright[/math] |
- Для доказательства достаточно рассмотреть алгоритм Форда-Фалкерсона для поиска максимального потока. Алгоритм делает примерно следующее (подробней — читай в соответствующей статье):
- В начале берем какой-нибудь поток за начальный (например, нулевой).
- В остаточной сети этого потока находим какой-нибудь путь из источника к стоку и увеличиваем поток на пропускную способность этого пути.
- Повторяем пункт [math]2[/math] до тех пор, пока находится хоть какой-то путь в остаточной сети.
- То, что получится в конце, будет максимальным потоком. В случае целочисленной сети достаточно в качестве начального приближения взять нулевой поток, и не трудно видеть, что на каждой итерации (в том числе и последней) этот поток будет оставаться целочисленным, что и докажет требуемое.
|
| [math]\triangleleft[/math] |
И, наконец, сделаем немного более осознанным в общем-то и так интуитивно понятное утверждение:
| Утверждение: |
Если в сети, где все пропускные способности ребер равны [math]1[/math], существует целочисленный поток величиной [math]L[/math] то существует и [math]L[/math] реберно непересекающихся путей. |
| [math]\triangleright[/math] |
- Считаем, что [math]u[/math] — источник, [math]v[/math] — сток.
- В начале поймем, что если поток не нулевой, то существует маршрут из [math]u[/math] в [math]v[/math] лежащий только на ребрах с потоком равным [math]1[/math]. В самом деле, если бы такого маршрута не существовало, то можно было бы выделить множество вершин до которых такие маршруты из вершины [math]u[/math] существуют, не включающее [math]v[/math], и по нему построить разрез. Поток через такой разрез, очевидно равен нулю, видим противоречие (т.к. [math]f(U,V)=|f|[/math], смотри первую лемму).
- Итак, найдем какой-нибудь маршрут из [math]u[/math] в [math]v[/math] лежащий только на ребрах где поток равен [math]1[/math]. Удалив все ребра находящиеся в этом маршруте и оставив все остальное неизменным, придем к целочисленному потоку величиной [math]L-1[/math]. Ясно, что можно повторить тоже самое еще [math]L-1[/math] раз, и, таким образом мы выделим [math]L[/math] реберно непересекающихся маршрутов.
|
| [math]\triangleleft[/math] |
Теорема
Теперь сама теорема будет тривиальным следствием. В начале сформулируем и докажем реберную версию для случая ориентированного графа.
| Теорема (Менгера о реберной двойственности в ориентированном графе): |
Между вершинами [math]u[/math] и [math]v[/math] существует [math]L[/math] реберно непересекающихся путей тогда и только тогда, когда после удаления любых [math](L-1)[/math] ребер существует путь из [math]u[/math] в [math]v[/math]. |
| Доказательство: |
| [math]\triangleright[/math] |
|
[math]\Leftarrow[/math]
- Как и прежде, пусть [math]u[/math] — источник, а [math]v[/math] — сток.
- Назначим каждому ребру пропускную способность [math]1[/math]. Тогда существует максимальный поток, целочисленный на каждом ребре (по лемме).
- По теореме Форда-Фалкерсона для такого потока существует разрез с пропускной способностью равной потоку. Удалим в этом разрезе [math]L-1[/math] ребер, и тогда, раз [math]u[/math] и [math]v[/math] находятся в разных частях разреза и, существует путь из [math]u[/math] в [math]v[/math], то в разрезе останется хотя бы еще одно ребро. Это значит, что пропускная способность разреза и вместе с ним величина потока не меньше [math]L[/math]. А так как поток целочисленный, то это и означает, что найдется [math] L[/math] реберно непересекающихся путей.
[math]\Rightarrow[/math]
- Существует [math] L[/math] реберно непересекающихся путей, а значит, удалив любые [math]L-1[/math] ребер хотя бы один путь останется не тронутым (принцип Дирихле). Это и означает, что существует путь из [math]u[/math] в [math]v[/math].
|
| [math]\triangleleft[/math] |
| Теорема (Менгера о вершинной двойственности в ориентированном графе): |
Между вершинами [math]u[/math] и [math]v[/math] существует [math]L[/math] вершинно непересекающихся путей тогда и только тогда, когда после удаления любых [math](L-1)[/math] вершин существует путь из [math]u[/math] в [math]v[/math]. |
| Доказательство: |
| [math]\triangleright[/math] |
- Разобьем каждую вершину на две таким образом:
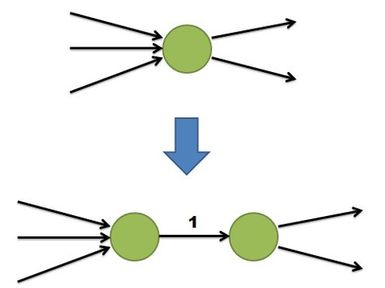
- (все входящие ребра заходят в левую вершину, исходящие выходят из правой. между двумя новыми вершинами добавляем ребро)
- Теперь задача практически сведена к первой теореме.
- Необходимо лишь отметить, что если в старом графе пути вершинно пересекаются, то в новом графе пути необходимо реберно пересекаются и наоборот.
- Кроме того, предложение "удалить в исходном графе любые [math]L[/math] вершин" можно заменять на "в новом графе можно удалить любые [math]L[/math] ребер" (достаточно выбирать вершины на концах этих ребер). Можно заменять и обратно, если учесть, что можно удалять ребра между парой вершин, которые раньше были одним целым.
|
| [math]\triangleleft[/math] |
См. такжеИсточники информации
- Ловас Л., Пламмер М. — Прикладные задачи теории графов. Теория паросочетаний в математике, физике, химии (глава 2.4 стр. 117) — 1998. — 656 с. — ISBN 5-03-002517-0
- Харари Ф. Теория графов. глава 5 — М.: Мир, 1973. (Изд. 3, М.: КомКнига, 2006. — 296 с.)
