Алгоритм Бржозовского — различия между версиями
(→Пример работы) |
|||
| Строка 24: | Строка 24: | ||
===Корректность=== | ===Корректность=== | ||
==Пример работы== | ==Пример работы== | ||
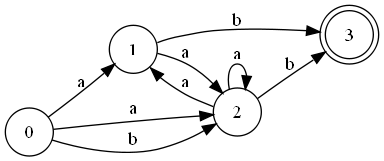
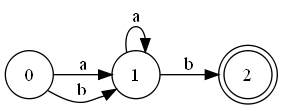
| + | * Исходный НКА | ||
| + | [[Файл:Fa.png|Исходный НКА]] | ||
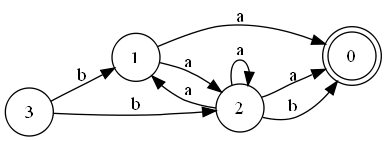
| + | * Первый шаг алгоритма | ||
| + | [[Файл:Rfa.png|Первый шаг]] | ||
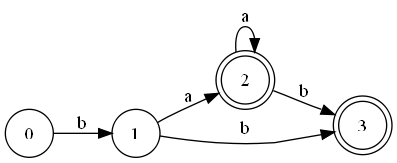
| + | * Второй шаг алгоритма | ||
| + | [[Файл:Drfa.png|Второй шаг]] | ||
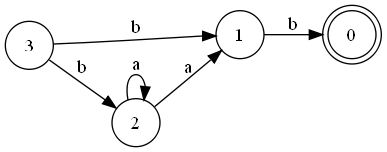
| + | * Третий шаг алгоритма | ||
| + | [[Файл:Rdrfa.png|Третий шаг]] | ||
| + | * Заключительный шаг алгоритма | ||
| + | [[Файл:Drdrfa.png|Заключительный шаг]] | ||
| + | |||
== См. также == | == См. также == | ||
*[[Минимизация ДКА, алгоритм за O(n^2) с построением пар различимых состояний]] | *[[Минимизация ДКА, алгоритм за O(n^2) с построением пар различимых состояний]] | ||
Версия 00:58, 27 декабря 2014
Эта статья находится в разработке!
| Задача: |
| Пусть дан автомат . Требуется построить автомат с наименьшим количеством состояний, распознающий тот же язык, что и . |
Алгоритм
Описание
Алгоритм минимизации конечных автоматов Бржозовского (Janusz A. (John) Brzozowski) выделяется, по крайней мере, следующими качествами:
- Он элегантен и весьма оригинален.
- Он эффективен.
- Он работает даже с недетерминированными конечными автоматами.
Обладая обычными процедурами обращения и детерминизации конечного автомата, мы, с помощью идеи Бржозовского, можем немедленно приступить к минимизации заданного автомата. Для этого надо дважды провести его через обе вышеуказанные процедуры:
, где
- это исходный КА,
- это процедура обращения КА,
- это процедура детерминизации КА,
- это минимизированный КА.
Корректность
Пример работы
- Исходный НКА
- Первый шаг алгоритма
- Второй шаг алгоритма
- Третий шаг алгоритма
- Заключительный шаг алгоритма
См. также
- Минимизация ДКА, алгоритм за O(n^2) с построением пар различимых состояний
- Минимизация ДКА, алгоритм Хопкрофта (сложность O(n log n))