Алгоритм Бржозовского
| Задача: |
| Пусть дан автомат . Требуется построить автомат с наименьшим количеством состояний, распознающий тот же язык, что и . |
Содержание
Описание
Пусть — состояние автомата .
| Определение: |
| Правым языком (англ. right language) называется язык , распознаваемый автоматом , в котором является уникальным начальным состоянием. |
| Определение: |
| Левым языком (англ. left language) называется язык , распознаваемый автоматом , в котором является уникальным терминальным состоянием. |
Таким образом, допустимые слова языка , проходящие через состояние , фактически разделяются на два языка, а соединение соответствующих слов этих языков по всем состояниям даст исходный язык .
Рассмотрим слово из левого языка . Тогда множество слов — правый контекст слова в языке . Аналогично для правого языка и левого контекста.
| Утверждение (1): |
Автомат является детерминированным тогда и только тогда, когда левые языки его состояний попарно не пересекаются. |
|
Рассмотрим состояния и () в ДКА. Пусть левые языки этих состояний пересекаются, то есть . По окончании процесса допуска слова мы оказываемся в состоянии или . Следовательно, из какого-то состояния на пути в терминальное существует несколько различных переходов по одному из символов , а значит — НКА. Получаем противоречие. |
| Определение: |
| Обратное слово (англ. reverse of the word) для слова определяется следующим образом: и если , тогда , где . |
| Определение: |
| Обратный язык (англ. reverse of the language) для языка — язык . |
| Определение: |
| Обратный автомат (англ. reverse of the automaton) для автомата — автомат , полученный из сменой местами начальных и конечных состояний и сменой направлений переходов. |
| Утверждение (2): |
Если распознает язык , то распознает . |
| Утверждение (3): |
Если левый язык состояния в — , тогда его левый язык в — . Аналогично для правого языка . |
Пусть — НКА.
Тогда детерминированный автомат определяется следующим образом:
- Детерминированному состоянию соответствует множество недетерминированных состояний: для каждого имеем ,
- Начальное состояние в — множество из начальных состояний автомата ,
- Состояние в детерминированном автомате является терминальным тогда и только тогда, когда оно содержится хотя бы в одном недетерминированном состоянии,
- Пусть — состояние детерминированного автомата и – символ из . Если переход из по символу определен, тогда, по построению: .
| Утверждение (4): |
Правый язык состояния эквивалентен объединению правых языков состояний автомата , принадлежащих множеству . |
| Определение: |
| Левое отношение (англ. left quotient) регулярного языка для слова из — язык . |
Минимальный автомат для регулярного языка определяется следующим образом:
- множество состояний — это множество левых отношений языка ,
- начальное состояние — ,
- терминальные состояния — множество отношений, содержащих пустое слово,
- функция перехода .
Автомат уникален с точностью до изоморфизма и имеет минимальное количество состояний.
| Утверждение (5): |
Детерминированный автомат минимален тогда и только тогда, когда правые языки его состояний различны и все состояния достижимы. |
|
Рассмотрим состояния и () в ДКА. Пусть их правые языки . Тогда состояния и можно объединить в одно. |
Алгоритм
Описание
Алгоритм минимизации конечных автоматов Бржозовского (Janusz A. (John) Brzozowski) выделяется, по крайней мере, следующими качествами:
- Он элегантен и весьма оригинален.
- Он эффективен.
- Он работает даже с недетерминированными конечными автоматами.
Введём следующие обозначения:
- — конечный автомат,
- — детерминизированный автомат для ,
- — обратный автомат для ,
- — результат . Аналогично для и .
| Теорема (Бржозовский, 1962): |
Пусть — автомат (необязательно детерминированный), распознающий язык . Минимальный детерминированный автомат может быть вычислен следующим образом: . |
| Доказательство: |
|
По построению автомат детерминированный. Согласно утверждению 2, он распознает язык . |
Пример работы
- Исходный НКА :
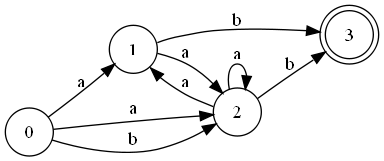
- Первый шаг, :
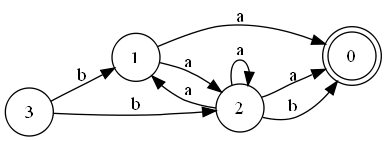
- Второй шаг, :
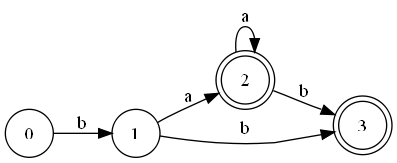
В детерминизированных автоматах состояния переименованы, так что всегда является начальным состоянием. - Третий шаг, :
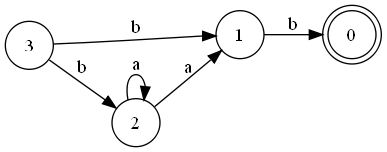
После выполнения этого шага алгоритма оба состояния и являются начальными. - Заключительный шаг, :
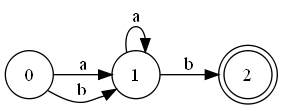
Заключение
Самым эффективным алгоритмом минимизации принято считать алгоритм Хопкрофта, который, как и прочие традиционные алгоритмы, работает только с ДКА. Его асимптотическое время выполнения зависит от логарифма исходных данных. С другой стороны очевидно, что алгоритм Бржозовского в худшем случае будет обладать экспоненциальным временем выполнения, ведь этого требует процедура детерминизации, выполняемая дважды. На практике же наблюдается парадокс, алгоритм Бржозовского во многих случаях опережает прочие подходы к минимизации, включая и алгоритм Хопкрофта. В работе[1], сравнивающей оба алгоритма, показано, что алгоритм Бржозовского оказывается эффективнее алгоритма Хопкрофта для автоматов с большим числом переходов.
См. также
- Минимизация ДКА, алгоритм за O(n^2) с построением пар различимых состояний
- Минимизация ДКА, алгоритм Хопкрофта (сложность O(n log n))