Матрица Кирхгофа — различия между версиями
| Строка 53: | Строка 53: | ||
*[[Связь матрицы Кирхгофа и матрицы инцидентности|Связь с матрицей инцидентности]]: | *[[Связь матрицы Кирхгофа и матрицы инцидентности|Связь с матрицей инцидентности]]: | ||
:<tex> K = I \cdot I^T, </tex> где <tex>I</tex> — матрица инцидентности некоторой ориентации графа. | :<tex> K = I \cdot I^T, </tex> где <tex>I</tex> — матрица инцидентности некоторой ориентации графа. | ||
| − | *<tex>0</tex> является собственным значением матрицы, кратность его равна числу | + | *<tex>0</tex> является собственным значением матрицы, кратность его равна числу компонент связности графа. |
Версия 16:32, 29 декабря 2014
| Определение: |
| Матрицей Кирхгофа простого графа называется матрица , элементы которой определяются равенством: |
Иными словами, на главной диагонали матрицы Кирхгофа находятся степени вершин, а на пересечении -й строки и -го столбца () стоит , если вершины с номерами и смежны, и в противном случае.
Пример матрицы Кирхгофа
| Граф | Матрица Кирхгофа |
|---|---|
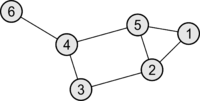
|
Некоторые свойства
- Сумма элементов каждой строки (столбца) матрицы Кирхгофа равна нулю:
- .
- Определитель матрицы Кирхгофа равен нулю:
- Матрица Кирхгофа простого графа симметрична:
- .
- Связь с матрицей смежности:
где — матрица смежности графа .
- где — матрица инцидентности некоторой ориентации графа.
- является собственным значением матрицы, кратность его равна числу компонент связности графа.
См. также
- Связь матрицы Кирхгофа и матрицы инцидентности
- Подсчет числа остовных деревьев с помощью матрицы Кирхгофа
Источники
- Асанов М., Баранский В., Расин В.: Дискретная математика: Графы, матроиды, алгоритмы
- Википедия, Матрица Кирхгофа