Вершинная, рёберная связность, связь между ними и минимальной степенью вершины — различия между версиями
Rost (обсуждение | вклад) |
|||
| Строка 16: | Строка 16: | ||
<tex>\varkappa \le\lambda \le \delta </tex> | <tex>\varkappa \le\lambda \le \delta </tex> | ||
|proof= | |proof= | ||
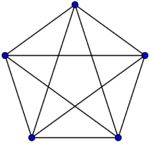
| + | [[Файл:K5.png|thumb|right|150x150px|Полный граф. <tex> \lambda = \delta = \varkappa = 4</tex>]] | ||
1) Проверим второе неравенство. Если в графе G нет ребер, то <tex> \lambda = 0 </tex>. Если ребра есть, то несвязный граф получаем из данного, удаляя все ребра, инцидентные вершине с наименьшей степенью. В любом случае <tex> \lambda \le \delta </tex>. <br/> | 1) Проверим второе неравенство. Если в графе G нет ребер, то <tex> \lambda = 0 </tex>. Если ребра есть, то несвязный граф получаем из данного, удаляя все ребра, инцидентные вершине с наименьшей степенью. В любом случае <tex> \lambda \le \delta </tex>. <br/> | ||
2) Чтобы проверить первое неравенство нужно рассмотреть несколько случаев. Если '''G''' - несвязный или тривиальный граф, то <tex> \varkappa = \lambda = 0 </tex>. Если G связен и имеет мост x, то <tex>\lambda = 1 </tex>. В последнем случае <tex> \varkappa = 1 </tex>, поскольку или граф G имеет точку сочленения, инцидентную ребру x, или же G = K<sub>2</sub>. Наконец, предположим, что граф G содержит множество из <tex> \lambda \ge 2 </tex> ребер, удаление которых делает его несвязным. Ясно, что удаляя <tex>\lambda - 1 </tex> ребер из этого множества получаем граф, имеющий мост x = uv. Для каждого из этих <tex>\lambda - 1 </tex> ребер выберем какую-либо инцидентную с ним вершину отличную от u и v. Удаление выбранных вершин приводит к удалению <tex>\lambda - 1 </tex> (а возможно, и большего числа) ребер. Если получаемый после такого удаления граф не связен, то <tex>\varkappa < \lambda </tex>; если же он связен, то в нем есть мост x, и поэтому удаление вершины u или ''v'' приводит либок несвязному, либо к тривиальному графу. в любом случае <tex> \varkappa \le \lambda</tex>. | 2) Чтобы проверить первое неравенство нужно рассмотреть несколько случаев. Если '''G''' - несвязный или тривиальный граф, то <tex> \varkappa = \lambda = 0 </tex>. Если G связен и имеет мост x, то <tex>\lambda = 1 </tex>. В последнем случае <tex> \varkappa = 1 </tex>, поскольку или граф G имеет точку сочленения, инцидентную ребру x, или же G = K<sub>2</sub>. Наконец, предположим, что граф G содержит множество из <tex> \lambda \ge 2 </tex> ребер, удаление которых делает его несвязным. Ясно, что удаляя <tex>\lambda - 1 </tex> ребер из этого множества получаем граф, имеющий мост x = uv. Для каждого из этих <tex>\lambda - 1 </tex> ребер выберем какую-либо инцидентную с ним вершину отличную от u и v. Удаление выбранных вершин приводит к удалению <tex>\lambda - 1 </tex> (а возможно, и большего числа) ребер. Если получаемый после такого удаления граф не связен, то <tex>\varkappa < \lambda </tex>; если же он связен, то в нем есть мост x, и поэтому удаление вершины u или ''v'' приводит либок несвязному, либо к тривиальному графу. в любом случае <tex> \varkappa \le \lambda</tex>. | ||
| Строка 21: | Строка 22: | ||
{{Теорема | {{Теорема | ||
|statement= | |statement= | ||
| − | Для любых натуральных чисел a, b, c, таких что a ≤ b ≤ c, существует граф G, у которого <tex>\varkappa = a, \lambda = b</tex> и <tex>\delta = c </tex> | + | Для любых натуральных чисел a, b, c, таких что a ≤ b ≤ c, существует граф G, у которого <tex>\varkappa = a, \lambda = b</tex> и <tex>\delta = c </tex> |
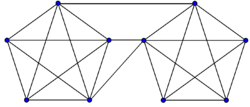
| − | |proof= | + | |proof=[[Файл:LambdaKappaDeltaGraph.png|thumb|left|250x600px|Граф, в котором <tex> \delta = 4</tex>, <tex>\lambda = 3</tex>, <tex>\varkappa = 2</tex>.]]Рассмотрим граф G, являющийся объединением двух полных графов <tex>G_1</tex> и <tex>G_2</tex>, содержащих c + 1 вершину. Отметим b вершин, принадлежащих подграфу <tex>G_1</tex> и a вершин, принадлежащих подграфу <tex>G_2</tex>. Добавим в граф G b ребер так, чтобы каждое ребро было инцидентно помеченной вершине, лежащей в подграфе <tex>G_1</tex> и помеченной вершине, лежащей в подграфе <tex>G_2</tex>, причем не осталось ни одной помеченной вершины, у которой не появилось хотя бы одно новое ребро, инцидентное ей. |
| − | |||
Тогда: <br> | Тогда: <br> | ||
1) Поскольку b ≤ c, то было как минимум две непомеченные вершины, поэтому <tex> \delta</tex> = с, так как минимальные степени вершин графов <tex>G_1</tex> и <tex>G_2</tex> была c, а степени их вершин не уменьшались.<br> | 1) Поскольку b ≤ c, то было как минимум две непомеченные вершины, поэтому <tex> \delta</tex> = с, так как минимальные степени вершин графов <tex>G_1</tex> и <tex>G_2</tex> была c, а степени их вершин не уменьшались.<br> | ||
| Строка 31: | Строка 31: | ||
== Литература == | == Литература == | ||
| − | * Харари Фрэнк '''Теория графов''' = Graph theory/Пер. с англ. и предисл. В. П. Козырева. Под ред. Г.П.Гаврилова. Изд. | + | * Харари Фрэнк '''Теория графов''' = Graph theory/Пер. с англ. и предисл. В. П. Козырева. Под ред. Г.П.Гаврилова. Изд. 4-е. ISBN 978-5-397-00622-4 |
| − | |||
[[Категория: Алгоритмы и структуры данных]] | [[Категория: Алгоритмы и структуры данных]] | ||
[[Категория: Связность в графах]] | [[Категория: Связность в графах]] | ||
Версия 07:44, 25 октября 2010
Определения
| Определение: |
| Вершинной связностью графа G называется наименьшее число вершин, удаление которых приводит к несвязному или тривиальному графу. |
| Определение: |
| Реберной связностью графа G называется наименьшее количество ребер, удаление которых приводит к несвязному или тривиальному графу. |
Связь между , и минимальной степенью вершины
Пускай минимальная степень вершины графа G обозначается буквой . Тогда:
| Теорема: |
Для любого графа G справедливо следующее неравенство: |
| Доказательство: |
|
1) Проверим второе неравенство. Если в графе G нет ребер, то . Если ребра есть, то несвязный граф получаем из данного, удаляя все ребра, инцидентные вершине с наименьшей степенью. В любом случае . |
| Теорема: |
Для любых натуральных чисел a, b, c, таких что a ≤ b ≤ c, существует граф G, у которого и |
| Доказательство: |
|
Рассмотрим граф G, являющийся объединением двух полных графов и , содержащих c + 1 вершину. Отметим b вершин, принадлежащих подграфу и a вершин, принадлежащих подграфу . Добавим в граф G b ребер так, чтобы каждое ребро было инцидентно помеченной вершине, лежащей в подграфе и помеченной вершине, лежащей в подграфе , причем не осталось ни одной помеченной вершины, у которой не появилось хотя бы одно новое ребро, инцидентное ей.
Тогда: |
Литература
- Харари Фрэнк Теория графов = Graph theory/Пер. с англ. и предисл. В. П. Козырева. Под ред. Г.П.Гаврилова. Изд. 4-е. ISBN 978-5-397-00622-4