Теорема Эдмондса-Лоулера — различия между версиями
(→Условие теоремы) |
(→Условие теоремы) |
||
| Строка 3: | Строка 3: | ||
|about= | |about= | ||
Эдмондса - Лоулера | Эдмондса - Лоулера | ||
| − | |statement= Пусть <tex>M_1=\langle X, I_1\rangle</tex>, <tex>M_2=\langle X, I_2\rangle</tex> | + | |statement= Пусть <tex>M_1=\langle X, I_1\rangle</tex>, <tex>M_2=\langle X, I_2\rangle</tex> {{---}} матроиды. Тогда <br> |
<tex>\max\limits_{I \in I_1 \cap I_2 } |I| = \min\limits_{A \subseteq X} \left(r_1(A) + r_2(X \setminus A)\right)</tex>. | <tex>\max\limits_{I \in I_1 \cap I_2 } |I| = \min\limits_{A \subseteq X} \left(r_1(A) + r_2(X \setminus A)\right)</tex>. | ||
| − | Где <tex>r_1</tex> и <tex>r_2</tex> | + | Где <tex>r_1</tex> и <tex>r_2</tex> {{---}} ранговые функции в первом и втором матроиде соответственно. |
|proof= | |proof= | ||
[[Файл:El_graph2.png|thumb|140px|right|Граф замен, кратчайший путь]] | [[Файл:El_graph2.png|thumb|140px|right|Граф замен, кратчайший путь]] | ||
| Строка 16: | Строка 16: | ||
<tex>|I| = |I \cap A| + |I \cap (X \setminus A)|</tex> | <tex>|I| = |I \cap A| + |I \cap (X \setminus A)|</tex> | ||
| − | <tex>I \cap A</tex> и <tex>I \cap (X \setminus A)</tex> - независимые в обоих матроидах (как подмножества независимового <tex>I</tex>), значит | + | <tex>I \cap A</tex> и <tex>I \cap (X \setminus A)</tex> {{---}} независимые в обоих матроидах (как подмножества независимового <tex>I</tex>), значит |
<tex>|I| = r_1(I \cap A) + r_2(I \cap (X \setminus A))</tex> | <tex>|I| = r_1(I \cap A) + r_2(I \cap (X \setminus A))</tex> | ||
| Строка 33: | Строка 33: | ||
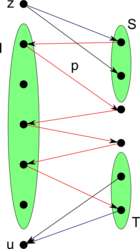
Обозначим <tex>S = \left\{x|I \cup \{x\} \in I_1\right\}</tex>, <tex>T = \left\{x|I \cup \{x\} \in I_2\right\}</tex>. Если <tex>S \cap T \ne \varnothing</tex>, добавим их пересечение в <tex>I</tex>. | Обозначим <tex>S = \left\{x|I \cup \{x\} \in I_1\right\}</tex>, <tex>T = \left\{x|I \cup \{x\} \in I_2\right\}</tex>. Если <tex>S \cap T \ne \varnothing</tex>, добавим их пересечение в <tex>I</tex>. | ||
| − | Построим [[Граф замен для двух матроидов|граф замен]] <tex>G_I</tex>. Добавим вершину <tex>z</tex>, не влияющую на независимость в первом матроиде | + | Построим [[Граф замен для двух матроидов|граф замен]] <tex>G_I</tex>. Добавим вершину <tex>z</tex>, не влияющую на независимость в первом матроиде {{---}} из неё будут вести рёбра во все вершины множества <tex>S</tex>. Пусть <tex>p</tex> {{---}} кратчайший путь из <tex>S</tex> в <tex>T</tex>, <tex>p_1</tex> {{---}} путь <tex>p</tex> с добавленным в начало ребром из <tex>z</tex>. По [[Лемма о единственном паросочетании в графе замен|лемме о единственном паросочетании]] и [[Лемма о единственном паросочетании в подграфе замен, индуцированном кратчайшим путем|лемме о единственном паросочетании, индуцированном кратчайшем путём]] <tex>I \bigtriangleup p_1 \in I_2</tex>. Теперь добавим вершину <tex>u</tex>, не влияющую на независимость во втором матроиде {{---}} в неё будут вести рёбра из всех вершин множества <tex>T</tex>. Тогда <tex>p_2</tex> (путь <tex>p</tex> с добавленным ребром в <tex>u</tex>) — кратчайший путь из <tex>S</tex> в <tex>u</tex>. Аналогично, <tex>I \bigtriangleup p_2 \in I_1</tex>. Отсюда следует, что <tex>I \bigtriangleup p \in I_1 \cap I_2</tex>, причём <tex>|I \bigtriangleup p| = |I| + 1</tex>.</div> |
Будем таким образом увеличивать <tex>I</tex>, пока существует путь <tex>p</tex>. Рассмотрим момент, когда такого пути не нашлось. | Будем таким образом увеличивать <tex>I</tex>, пока существует путь <tex>p</tex>. Рассмотрим момент, когда такого пути не нашлось. | ||
Версия 21:52, 7 июня 2015
Условие теоремы
| Теорема (Эдмондса - Лоулера): |
Пусть , — матроиды. Тогда . Где и — ранговые функции в первом и втором матроиде соответственно. |
| Доказательство: |
|
Докажем неравенство Выберем произвольные , , тогда
и — независимые в обоих матроидах (как подмножества независимового ), значит
Но и , значит
В силу произвольности и получаем
Обозначим , . Если , добавим их пересечение в . Построим граф замен . Добавим вершину , не влияющую на независимость в первом матроиде — из неё будут вести рёбра во все вершины множества . Пусть — кратчайший путь из в , — путь с добавленным в начало ребром из . По лемме о единственном паросочетании и лемме о единственном паросочетании, индуцированном кратчайшем путём . Теперь добавим вершину , не влияющую на независимость во втором матроиде — в неё будут вести рёбра из всех вершин множества . Тогда (путь с добавленным ребром в ) — кратчайший путь из в . Аналогично, . Отсюда следует, что , причём .Будем таким образом увеличивать , пока существует путь . Рассмотрим момент, когда такого пути не нашлось. Введём обозначение: . Докажем, что от противного. Пусть , тогда существует , такое, что . Если , то и из есть путь в . Значит, . Отсюда следует, что существует , такое что . Но тогда ребро имеется в графе, то есть из существует путь в , что противоречит условию . Следовательно, . Аналогично, . Отсюда , то есть при найденных и достигается равенство. Построен пример равенства, значит, теорема доказана. |
Источник
Chandra Chekuri — Combinatorial Optimization, c. 2-4