|
|
| Строка 7: |
Строка 7: |
| | '''Необходимость'''<br/> | | '''Необходимость'''<br/> |
| | Докажем, что <tex>G</tex> можно покрыть <tex>N</tex> реберно-простыми путями.<br/> | | Докажем, что <tex>G</tex> можно покрыть <tex>N</tex> реберно-простыми путями.<br/> |
| − | Добавим в <tex>G</tex> <tex> N </tex> ребер <tex>uv</tex> таких, что <tex>uv</tex> <tex>\notin</tex> <tex>G</tex> и степени вершин <tex>u</tex> и <tex>v</tex> нечетные. Тогда степени всех вершин станут четными, и в <tex>G</tex> появится Эйлеров цикл <tex>c</tex>. Удалим из <tex>c</tex> добавленные ребра.<br/> | + | Добавим <tex> N </tex> ребер <tex>uv</tex> таких, что <tex>uv</tex> <tex>\notin</tex> <tex>G</tex> и степени вершин <tex>u</tex> и <tex>v</tex> нечетные. Тогда степени всех вершин станут четными, и в <tex>G</tex> появится Эйлеров цикл <tex>c</tex>. Удалим из <tex>c</tex> добавленные ребра.<br/> |
| | Заметим, что теперь цикл распадается на <tex> N </tex> простых путей. В самом деле: отметим удаленные ребра в порядке их обхода в Эйлеровом цикле. Тогда <tex> c </tex> разбивается на <tex> N </tex> реберно-непересекающихся путей, т.к. каждый такой путь мы можем сопоставить удаленному ребру. Необходимость доказана. | | Заметим, что теперь цикл распадается на <tex> N </tex> простых путей. В самом деле: отметим удаленные ребра в порядке их обхода в Эйлеровом цикле. Тогда <tex> c </tex> разбивается на <tex> N </tex> реберно-непересекающихся путей, т.к. каждый такой путь мы можем сопоставить удаленному ребру. Необходимость доказана. |
| | | | |
Версия 16:47, 14 января 2016
Следующее утверждение являются следствием из критерия Эйлеровости графа:
| Теорема: |
Пусть [math]G[/math] — граф, в котором [math]2N[/math] вершин имеют нечетную степень. Тогда множество ребер [math]G[/math] можно покрыть [math]N[/math] реберно-простыми путями. |
| Доказательство: |
| [math]\triangleright[/math] |
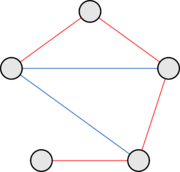 Пример графа для [math]N = 2[/math]Необходимость
Докажем, что [math]G[/math] можно покрыть [math]N[/math] реберно-простыми путями.
Добавим [math] N [/math] ребер [math]uv[/math] таких, что [math]uv[/math] [math]\notin[/math] [math]G[/math] и степени вершин [math]u[/math] и [math]v[/math] нечетные. Тогда степени всех вершин станут четными, и в [math]G[/math] появится Эйлеров цикл [math]c[/math]. Удалим из [math]c[/math] добавленные ребра.
Заметим, что теперь цикл распадается на [math] N [/math] простых путей. В самом деле: отметим удаленные ребра в порядке их обхода в Эйлеровом цикле. Тогда [math] c [/math] разбивается на [math] N [/math] реберно-непересекающихся путей, т.к. каждый такой путь мы можем сопоставить удаленному ребру. Необходимость доказана.
Достаточность
Докажем, что [math]G[/math] нельзя покрыть менее, чем [math]N[/math] реберно-простыми путями.
Предположим, что такое возможно, и существует набор реберно-простых путей [math]p_1, p_2, ... p_k, k \lt N[/math], такой что он покрывает все ребра [math]G[/math].
Пусть [math]i-[/math]й путь из этого набора имеет вид [math] w_i = u_{i_0}e_{i_1}u_{i_1}...u_{i_l}[/math]. Добавим в [math]G[/math] все ребра вида [math]u_{i_l}u_{{i+1}_0}[/math] и ребро [math]u_{k_l}u_{1_0}[/math]. В новом графе появится Эйлеров цикл, т.к. мы добавили ребра, соединяющие конец и начало [math] i [/math] и [math] i + 1 [/math] пути соответственно. Всего добавлено [math]k[/math] ребер, которые меняют четность не более, чем [math]2k[/math] вершин. Т.к. [math]k \lt N[/math], то в графе останутся вершины нечетной степени, что не удовлетворяет критерию Эйлеровости графа.
Противоречие. Значит, такого набора, что его мощность меньше [math]N[/math], не существует. |
| [math]\triangleleft[/math] |
См. также
Источники информации
- Харари Фрэнк Теория графов = Graph theory/Пер. с англ. и предисл. В. П. Козырева. Под ред. Г.П.Гаврилова. Изд. 2-е. — М.: Едиториал УРСС, 2003. — 296 с. — ISBN 5-354-00301-6
