Несовпадение класса языков, распознаваемых ДМП автоматами и произвольными МП автоматами — различия между версиями
AReunov (обсуждение | вклад) |
|||
| Строка 8: | Строка 8: | ||
|statement=Классы языков, задаваемых МП-автоматами и ДМП-автоматами с допуском по допускающему состоянию не совпадают. | |statement=Классы языков, задаваемых МП-автоматами и ДМП-автоматами с допуском по допускающему состоянию не совпадают. | ||
|proof=[[Файл:pda_1.png|320px|thumb|right|Автомат <tex>M</tex>]][[Файл:pda_2.png|320px|thumb|right|Автомат <tex>M''</tex>]] | |proof=[[Файл:pda_1.png|320px|thumb|right|Автомат <tex>M</tex>]][[Файл:pda_2.png|320px|thumb|right|Автомат <tex>M''</tex>]] | ||
| − | Рассмотрим язык <tex>L=\left\{0^n1^n\right\} \cup \left\{0^n1^{2n}\right\}</tex>. | + | Рассмотрим язык <tex>L=\left\{0^n1^n\right\} \cup \left\{0^n1^{2n}\right\}</tex>. Очевидно, что язык <tex>L</tex> является контекстно-свободным. |
| − | Очевидно, что язык <tex>L</tex> является контекстно-свободным. | + | |
| − | + | <br> | |
| + | Так как множества языков, распознаваемых ДМП-автомат с допуском по допускающему состоянию и ДМП-автомат с допуском по пустому стеку совпадают(см. [[Детерминированные автоматы с магазинной памятью, допуск по пустому стеку | соответствующую теорему]]), будем рассматривать в доказательстве ДМП-автомат с допуском по допускающему состоянию. | ||
| − | Построим на основе <tex>M</tex> недетерминированный МП-автомат, распознающий язык <tex>L' = \left\{0^{n}1^{n}2^{n}\right\} \cup \left\{0^n1^n\right\} \cup \left\{0^n1^{2n}\right\}</tex>. Для начала построим по автомату <tex>M</tex> автомат <tex>M'</tex>, заменив все вхождения символа <tex>1</tex> на символ <tex>2</tex>. Далее объединим автоматы <tex>M</tex> и <tex>M'</tex> в автомат <tex>M''</tex>, соединив допускающие состояния <tex>\varepsilon</tex>-переходами (как показано на картинке). | + | <br> |
| + | Пусть существует ДМП-автомат с допуском по допускающему состоянию <tex>M</tex>, распознающий язык <tex>L</tex>. | ||
| + | В силу детерминированности автомата <tex>(s, z_0, 0^n1^{n})\vdash^*(q_1, \gamma_1, 1^n)\vdash^*(q_2, \gamma_2, \varepsilon)</tex>, причём <tex>q_1, q_2 \in T</tex>. | ||
| + | <br> | ||
| + | Рассмотрим также язык <tex>L''=\left\{0^n1^n2^n\right\}</tex>. | ||
| + | |||
| + | <br> | ||
| + | Построим на основе <tex>M</tex> недетерминированный МП-автомат, распознающий язык | ||
| + | :<tex>L' = \left\{0^{n}1^{n}2^{n}\right\} \cup \left\{0^n1^n\right\} \cup \left\{0^n1^{2n}\right\}</tex>. | ||
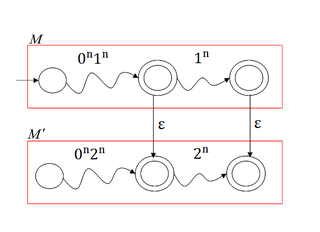
| + | # Для начала построим по автомату <tex>M</tex> автомат <tex>M'</tex>, заменив все вхождения символа <tex>1</tex> на символ <tex>2</tex>. | ||
| + | # Далее объединим автоматы <tex>M</tex> и <tex>M'</tex> в автомат <tex>M''</tex>, соединив допускающие состояния <tex>\varepsilon</tex>-переходами (как показано на картинке). | ||
| + | |||
| + | <br> | ||
Автомат <tex>M''</tex> является недетерминированным МП-автоматом, и принимает не контекстно-свободный язык <tex>L'</tex>. | Автомат <tex>M''</tex> является недетерминированным МП-автоматом, и принимает не контекстно-свободный язык <tex>L'</tex>. | ||
| + | |||
Полученное противоречие доказывает, что нет ДМП-автомата с допуском по допускающему состоянию, распознающего язык <tex>L</tex>. Но из того, что <tex>L</tex> — контекстно-свободный следует, что есть недетерминированный МП-автомат, распознающий его. | Полученное противоречие доказывает, что нет ДМП-автомата с допуском по допускающему состоянию, распознающего язык <tex>L</tex>. Но из того, что <tex>L</tex> — контекстно-свободный следует, что есть недетерминированный МП-автомат, распознающий его. | ||
}} | }} | ||
| + | |||
| + | == См. также == | ||
| + | * [[Автоматы с магазинной памятью]] | ||
| + | * [[МП-автоматы, допуск по пустому стеку и по допускающему состоянию, эквивалентность | Допуск по пустому стеку и по допускающему состоянию]] | ||
| + | * [[Детерминированные автоматы с магазинной памятью]] | ||
| + | |||
| + | == Источники информации == | ||
| + | * ''Хопкрофт Д., Мотвани Р., Ульман Д.'' Введение в теорию автоматов, языков и вычислений, 2-е изд. : Пер. с англ. — М.:Издательский дом «Вильямс», 2002. — С. 61.— ISBN 5-8459-0261-4 | ||
| + | *[https://ru.wikipedia.org/wiki/%D0%90%D0%B2%D1%82%D0%BE%D0%BC%D0%B0%D1%82_%D1%81_%D0%BC%D0%B0%D0%B3%D0%B0%D0%B7%D0%B8%D0%BD%D0%BD%D0%BE%D0%B9_%D0%BF%D0%B0%D0%BC%D1%8F%D1%82%D1%8C%D1%8E Википедия {{---}} Автомат с магазинной памятью] | ||
[[Категория: Теория формальных языков]] | [[Категория: Теория формальных языков]] | ||
[[Категория: Контекстно-свободные грамматики]] | [[Категория: Контекстно-свободные грамматики]] | ||
| + | [[Категория: МП-автоматы]] | ||
Версия 19:50, 14 января 2016
В отличие от конечных автоматов, для МП-автоматов недетерминизм является существенным. ДМП-автоматы распознают не все языки, распознаваемые МП-автоматами или КС-грамматиками.
| Лемма: |
Язык не является контекстно-свободным. |
| Доказательство: |
| Для фиксированного рассмотрим слово . Пусть разбили на произвольным образом. Так как , то в слове не содержится либо ни одного символа , либо ни одного символа . Для любого такого разбиения выбираем и получаем, что количество символов изменилось, а количество либо , либо осталось тем же. Очевидно, что такое слово не принадлежит рассмотренному языку. Значит, язык не является контекстно-свободным по лемме о разрастании для КС-грамматик. |
| Теорема: |
Классы языков, задаваемых МП-автоматами и ДМП-автоматами с допуском по допускающему состоянию не совпадают. |
| Доказательство: |
|
Рассмотрим язык . Очевидно, что язык является контекстно-свободным.
|
См. также
- Автоматы с магазинной памятью
- Допуск по пустому стеку и по допускающему состоянию
- Детерминированные автоматы с магазинной памятью
Источники информации
- Хопкрофт Д., Мотвани Р., Ульман Д. Введение в теорию автоматов, языков и вычислений, 2-е изд. : Пер. с англ. — М.:Издательский дом «Вильямс», 2002. — С. 61.— ISBN 5-8459-0261-4
- Википедия — Автомат с магазинной памятью