Детерминированные автоматы с магазинной памятью — различия между версиями
KK (обсуждение | вклад) м (→Пример) |
KK (обсуждение | вклад) м (→Пример) |
||
| Строка 8: | Строка 8: | ||
==Пример== | ==Пример== | ||
Построим для языка: | Построим для языка: | ||
| − | # <tex> S \rightarrow | + | # <tex> S \rightarrow 1H </tex> |
| − | # <tex> H \rightarrow | + | # <tex> H \rightarrow 0F </tex> |
| − | # <tex> | + | # <tex> F \rightarrow 0F </tex> |
| − | # <tex> | + | # <tex> F \rightarrow 1F </tex> |
| + | # <tex> F \rightarrow \varepsilon </tex> | ||
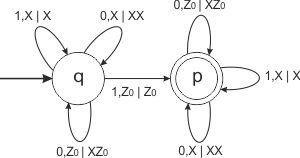
автомат <tex>A=(\{0,1\}, \{Z_0,X\}, \{q,p\}, q, \{p\}, Z_0, \delta)</tex> с функией перехода <tex>\delta</tex>: | автомат <tex>A=(\{0,1\}, \{Z_0,X\}, \{q,p\}, q, \{p\}, Z_0, \delta)</tex> с функией перехода <tex>\delta</tex>: | ||
# <tex>\delta(q,0,Z_0)=(q,XZ_0)</tex> | # <tex>\delta(q,0,Z_0)=(q,XZ_0)</tex> | ||
Версия 07:37, 17 января 2016
| Определение: |
Детерменированным автоматом с магазинной памятью (англ. deterministic pushdown automaton) называется автомат с магазинной памятью, для которого выполнены следующие условия:
|
Пример
Построим для языка:
автомат с функией перехода :
См. также
- Детерминированные автоматы с магазинной памятью, допуск по пустому стеку
- Несовпадение класса языков, распознаваемых ДМП автоматами и произвольными МП автоматами
- ДМП-автоматы и неоднозначность
Источники информации
- Хопкрофт Д., Мотвани Р., Ульман Д. — Введение в теорию автоматов, языков и вычислений, 2-е изд. : Пер. с англ. — Москва, Издательский дом «Вильямс», 2008. — 528с. : ISBN 978-5-8459-1347-0 (рус.)