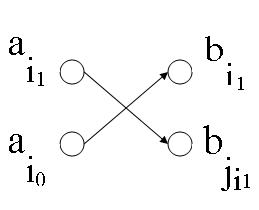Граф замен

Граф замен — специальный ориентированный двудольный граф, фигурирующий в теореме Эдмондса-Лоулера.

Пусть даны матроиды [math]M_1 = \langle S, \mathcal{I}_1 \rangle[/math], [math]M_2 = \langle S, \mathcal{I}_2 \rangle[/math], множество [math](\mathcal{I}_1 \cap \mathcal{I}_2)[/math]. Введем граф замен.

Определение:

Граф замен для двух матроидов [math]D_{M_1, M_2}(I)[/math] — граф, левой долей которого являются элементы множества [math]I[/math], правой — все остальные элементы [math]S[/math] и в котором проведены ребра [math](y, z): y \in I, z \in S \setminus I, I \setminus y \cup z \in \mathcal{I}_1[/math], а также [math](z', y'): y' \in I, z' \in S \setminus I, I \setminus y' \cup z' \in \mathcal{I}_2[/math]

Пусть [math]X_1 = \{z \in S \setminus I \mid I \cup z \in \mathcal{I}_1 \}, X_2 = \{z \in S \setminus I \mid I \cup z \in \mathcal{I}_2 \}, P[/math] — кратчайший путь в [math]D_{M_1, M_2}(I)[/math] из [math]X_1[/math] в [math]X_2[/math]. Тогда алгоритм с помощью этого пути либо определяет максимальность набора [math]I[/math], либо позволяет найти набор большей мощности.

Граф замен [math]D_{M_1, M_2}(I)[/math]

Также существует граф замен для одного матроида.

Определение:

Пусть дан матроид [math]M = (S, \mathcal{I})[/math] и независимый сет [math]I \in \mathcal{I}[/math]. Тогда граф замен [math]D_{M}(I)[/math] (или просто [math]D(I)[/math]) — это двудольный граф с долями [math]I[/math] и [math]S \setminus I[/math] с рёбрами между [math]y \in I[/math] и [math]x \in S \setminus I[/math] если [math] I - y + x \in \mathcal{I} [/math]

Лемма (о единственном паросочетании в подграфе замен, индуцированном кратчайшим путем):

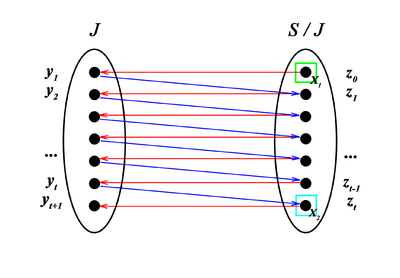
Пусть дан двудольный граф замен. В его правой доле можно выделить два подмножества вершин [math]X_1 = \{z \in S \setminus I \mid I \cup z \in \mathcal{I}_1 \}, X_2 = \{z \in S \setminus I \mid I \cup z \in \mathcal{I}_2 \}[/math]. Пусть [math]P[/math] — кратчайший путь из [math]X_1[/math] в [math]X_2[/math]. Рассмотрим сужение [math]G'[/math] графа [math]G[/math] на множество вершин, лежащих в пути [math]P[/math]. Тогда в [math]G'[/math] существует единственное полное паросочетание.

Доказательство:

[math]\triangleright[/math]

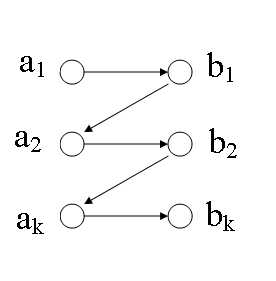
Рис. 1 Рис. 2 Строго говоря, утверждение теоремы не совсем корректно, так как в правой доле полученного графа [math]G'[/math] вершин на одну больше, чем в левой. Поэтому добавим в [math]G'[/math] фиктивную вершину и отнесем ее к левой доле. Пусть путь [math]P = (a_1, b_1, a_2, b_2, \ldots , a_k, b_k)[/math], где [math]a_1[/math] — фиктивная вершина (рис. 1). Существование полного паросочетания очевидно — это ребра [math](a_i,b_i)[/math]. Предположим, что существует другое паросочетание [math](a_i, b_{j_i})[/math]. Тогда пусть [math]i_0 = \min \{ i \: \mid \: j_i \lt i \}[/math]. Обозначим [math]j_{i_0}[/math] как [math]i_1[/math]. Заметим, что [math]i_1 \lt i_0[/math] и поэтому не может быть [math]j_{i_1} \lt i_1[/math], ведь [math]i_0[/math] — минимальное из соответствующего множества. Так же невозможно [math]j_{i_1} = i_1[/math], поскольку тогда [math]a_{i_0}[/math] и [math]a_{i_1}[/math] имели бы одинаковую пару. Следовательно, [math]j_{i_1} \gt i_1[/math] (рис. 2). Это значит, что существует путь [math]P_1 = (a_1, b_1, \ldots, a_{i_1}, b_{j_{i_1}}, a_{j_{i_1} + 1}, \ldots, a_k, b_k )[/math] короче, чем [math]P[/math]. Противоречие.

[math]\triangleleft[/math]

Лемма (о паросочетании в графе замен):

Пусть [math]M = \langle X,I \rangle [/math] — матроид. Множества [math]A, B \in I[/math] — независимы, причем [math]|A| = |B|[/math]. Тогда двудольный граф [math]D_{M}(I)[/math] содержит полное паросочетание на [math]A \bigtriangleup B[/math].

Доказательство:

[math]\triangleright[/math]

Индукция по [math]|A \bigtriangleup B|[/math]. База В случае, когда [math]|A \bigtriangleup B| = 0 [/math], это тривиальный случай, имеем пустое паросочетание. Переход Пусть [math]k = |A| = |B|[/math]. Рассмотрим [math]|A \bigtriangleup B| \geqslant 1[/math]. Рассмотрим матроид [math]M_1 = \langle X, \{ A \mid A \in I, A \leq k \} \rangle[/math]. Множества [math]A, B \in I[/math] и [math]|A| = |B|[/math], а значит они являются базами для матроида [math]M_1[/math]. По сильной теореме о базах [math]\forall x \in A \setminus B: \exists y \in B \setminus A : (A \setminus x) \cup y \in I[/math] и [math](B \setminus y) \cup x \in I[/math] из этого следует, что множество [math]A' = A - x + y [/math] и [math]B' = B + x - y[/math] являются независимыми, а также базами [math]M_1[/math]. И их [math]|A' \bigtriangleup B'| \lt |A \bigtriangleup B|[/math]. Значит мы умеем переходить от [math]|A' \bigtriangleup B'| = N[/math] к [math]|A \bigtriangleup B| = N+1[/math]. По предположению индукции у [math] |A' \bigtriangleup B'|[/math] есть полное паросочетание. По теореме о базах [math]\forall x \in A \setminus B: \exists y \in B \setminus A : (A \setminus x) \cup y \in I[/math], следовательно по определению графа [math]D_M(A) \Rightarrow (x, y) \in D_M(A)[/math]. Тогда [math]N \cup {(x, y)}[/math] составляет полное паросочетание на [math]|A \bigtriangleup B|[/math], а значит индукционный переход справедлив.

[math]\triangleleft[/math]

См. также

• Пересечение матроидов, определение, примеры
• Алгоритм построения базы в пересечении матроидов

Источники информации

• Chandra Chekuri — Combinatorial Optimization
• Michel X. Goemans — Matroid Intersection