Рекуррентные нейронные сети — различия между версиями
Adel (обсуждение | вклад) (Новая страница: «450px|thumb|[http://colah.github.io/posts/2015-08-Understanding-LSTMs/ RNN и ее развернутое представление] File:RNN_…») |
Adel (обсуждение | вклад) |
||
| Строка 27: | Строка 27: | ||
=== Полностью рекуррентная сеть === | === Полностью рекуррентная сеть === | ||
Это базовая архитектура, разработанная в 1980-х. Сеть строится из узлов, каждый из которых соединён со всеми другими узлами. У каждого нейрона порог активации меняется со временем и является вещественным числом. Каждое соединение имеет переменный вещественный вес. Узлы разделяются на входные, выходные и скрытые. | Это базовая архитектура, разработанная в 1980-х. Сеть строится из узлов, каждый из которых соединён со всеми другими узлами. У каждого нейрона порог активации меняется со временем и является вещественным числом. Каждое соединение имеет переменный вещественный вес. Узлы разделяются на входные, выходные и скрытые. | ||
| + | |||
=== Рекурсивная сеть === | === Рекурсивная сеть === | ||
[[:Рекурсивные нейронные сети|Рекурсивные нейронные сети]] представляют собой более общий случай рекуррентных сетей, когда сигнал в сети проходит через структуру в виде дерева (обычно бинарные деревья). Те же самые матрицы весов используются рекурсивно по всему графу в соответствии с его топологией. | [[:Рекурсивные нейронные сети|Рекурсивные нейронные сети]] представляют собой более общий случай рекуррентных сетей, когда сигнал в сети проходит через структуру в виде дерева (обычно бинарные деревья). Те же самые матрицы весов используются рекурсивно по всему графу в соответствии с его топологией. | ||
| + | |||
=== Нейронная сеть Хопфилда === | === Нейронная сеть Хопфилда === | ||
Тип рекуррентной сети, когда все соединения симметричны. Изобретена Джоном Хопфилдом в 1982 году и гарантируется, что динамика такой сети сходится к одному из положений равновесия. | Тип рекуррентной сети, когда все соединения симметричны. Изобретена Джоном Хопфилдом в 1982 году и гарантируется, что динамика такой сети сходится к одному из положений равновесия. | ||
| + | |||
=== Двунаправленная ассоциативная память (BAM) === | === Двунаправленная ассоциативная память (BAM) === | ||
Вариацией сети Хопфилда является двунаправленная ассоциативная память (BAM). BAM имеет два слоя, каждый из которых может выступать в качестве входного, находить (вспоминать) ассоциацию и генерировать результат для другого слоя. | Вариацией сети Хопфилда является двунаправленная ассоциативная память (BAM). BAM имеет два слоя, каждый из которых может выступать в качестве входного, находить (вспоминать) ассоциацию и генерировать результат для другого слоя. | ||
[[File:Elman_RNN.jpg|450px|thumb|Сеть Элмана]] | [[File:Elman_RNN.jpg|450px|thumb|Сеть Элмана]] | ||
| + | |||
=== Сеть Элмана === | === Сеть Элмана === | ||
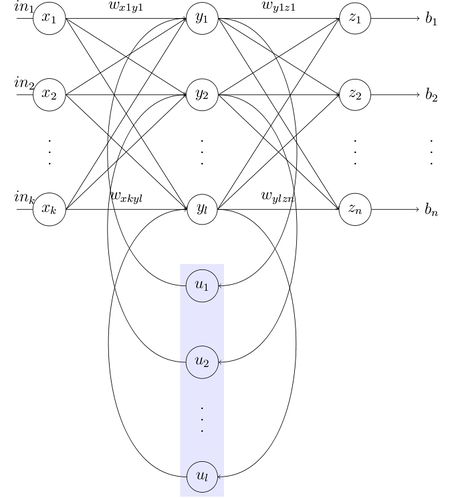
Нейронная сеть Элмана состоит из трёх слоев: x, y, z (см рис. Сеть Элмана). Дополнительно к сети добавлен набор «контекстных блоков»: u (см рис. Сеть Элмана). Средний (скрытый) слой соединён с контекстными блоками с фиксированным весом, равным единице. С каждым шагом времени на вход поступает информация, которая проходит прямой ход к выходному слою в соответствии с правилами обучения. Фиксированные обратные связи сохраняют предыдущие значения скрытого слоя в контекстных блоках (до того как скрытый слой поменяет значение в процессе обучения). Таким способом сеть сохраняет своё состояние, что может использоваться в предсказании последовательностей, выходя за пределы мощности многослойного перцептрона. | Нейронная сеть Элмана состоит из трёх слоев: x, y, z (см рис. Сеть Элмана). Дополнительно к сети добавлен набор «контекстных блоков»: u (см рис. Сеть Элмана). Средний (скрытый) слой соединён с контекстными блоками с фиксированным весом, равным единице. С каждым шагом времени на вход поступает информация, которая проходит прямой ход к выходному слою в соответствии с правилами обучения. Фиксированные обратные связи сохраняют предыдущие значения скрытого слоя в контекстных блоках (до того как скрытый слой поменяет значение в процессе обучения). Таким способом сеть сохраняет своё состояние, что может использоваться в предсказании последовательностей, выходя за пределы мощности многослойного перцептрона. | ||
| + | |||
| + | <math>h_t = \sigma_h(W_h x_t + U_h h_{t-1} + b_h)</math> | ||
| + | |||
| + | <math>y_t = \sigma_y(W_y h_t + b_y)</math> | ||
| + | |||
| + | Обозначения переменных и функций: | ||
| + | * <math>x_t</math>: вектор входного слоя | ||
| + | * <math>h_t</math>: вектор скрытого слоя | ||
| + | * <math>y_t</math>: вектор выходного слоя | ||
| + | * <math>W, U и b</math>: матрица и вектор параметров | ||
| + | * <math>\sigma_h и \sigma_y</math>: функция активации | ||
| + | |||
=== Сеть Джордана === | === Сеть Джордана === | ||
Нейронная сеть Джордана подобна сети Элмана, но контекстные блоки связаны не со скрытым слоем, а с выходным слоем. Контекстные блоки таким образом сохраняют своё состояние. Они обладают рекуррентной связью с собой. | Нейронная сеть Джордана подобна сети Элмана, но контекстные блоки связаны не со скрытым слоем, а с выходным слоем. Контекстные блоки таким образом сохраняют своё состояние. Они обладают рекуррентной связью с собой. | ||
| + | |||
| + | <math>h_t = \sigma_h(W_h x_t + U_h y_{t-1} + b_h)</math> | ||
| + | |||
| + | <math>y_t = \sigma_y(W_y h_t + b_y)</math> | ||
| + | |||
=== Эхо-сети === | === Эхо-сети === | ||
Эхо-сеть (англ. Echo State Network, ESN) характеризуется одним скрытым слоем (который называется резервуаром) со случайными редкими связями между нейронами. При этом связи внутри резервуара фиксированы, но связи с выходным слоем подлежат обучению. Состояние резервуара (state) вычисляется через предыдущие состояния резервуара, а также предыдущие состояния входного и выходного сигналов. Так как эхо-сети обладают только одним скрытым слоем, они обладают достаточно низкой вычислительной сложностью. | Эхо-сеть (англ. Echo State Network, ESN) характеризуется одним скрытым слоем (который называется резервуаром) со случайными редкими связями между нейронами. При этом связи внутри резервуара фиксированы, но связи с выходным слоем подлежат обучению. Состояние резервуара (state) вычисляется через предыдущие состояния резервуара, а также предыдущие состояния входного и выходного сигналов. Так как эхо-сети обладают только одним скрытым слоем, они обладают достаточно низкой вычислительной сложностью. | ||
| + | |||
=== Нейронный компрессор истории === | === Нейронный компрессор истории === | ||
Нейронный компрессор исторических данных {{---}} это блок, позволяющий в сжатом виде хранить существенные исторические особенности процесса, который является своего рода стеком рекуррентной нейронной сети, формируемым в процессе самообучения. | Нейронный компрессор исторических данных {{---}} это блок, позволяющий в сжатом виде хранить существенные исторические особенности процесса, который является своего рода стеком рекуррентной нейронной сети, формируемым в процессе самообучения. | ||
[[File:LSTM.png|450px|thumb|[http://colah.github.io/posts/2015-08-Understanding-LSTMs/ Схема слоев рекуррентной сети долго-краткосрочной памяти]]] | [[File:LSTM.png|450px|thumb|[http://colah.github.io/posts/2015-08-Understanding-LSTMs/ Схема слоев рекуррентной сети долго-краткосрочной памяти]]] | ||
| + | |||
=== Сети долго-краткосрочной памяти === | === Сети долго-краткосрочной памяти === | ||
Сеть долго-краткосрочной памяти (англ. Long short-term memory, LSTM) является самой популярная архитектура рекуррентной нейронной сети на данный момент, данная архитектура способна запоминать данные на долгое время.<ref name=LSTM>[https://www.bioinf.jku.at/publications/older/2604.pdf Sepp Hochreiter, Jurgen Schmidhuber. Long short-term memory (1997). Neural Computation.]</ref> | Сеть долго-краткосрочной памяти (англ. Long short-term memory, LSTM) является самой популярная архитектура рекуррентной нейронной сети на данный момент, данная архитектура способна запоминать данные на долгое время.<ref name=LSTM>[https://www.bioinf.jku.at/publications/older/2604.pdf Sepp Hochreiter, Jurgen Schmidhuber. Long short-term memory (1997). Neural Computation.]</ref> | ||
| Строка 50: | Строка 73: | ||
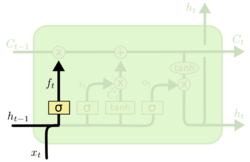
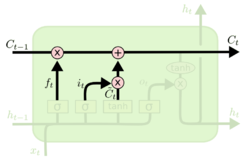
Первый слой вычисляет, насколько на данном шаге ему нужно забыть предыдущую информацию {{---}} по сути множители к компонентам вектора памяти. | Первый слой вычисляет, насколько на данном шаге ему нужно забыть предыдущую информацию {{---}} по сути множители к компонентам вектора памяти. | ||
[[File:LSTM_F1.png|none|250px]] | [[File:LSTM_F1.png|none|250px]] | ||
| − | <math>f_t = \sigma(W_f * [ | + | <math>f_t = \sigma(W_f * [h_{t-1}, x_t] + b_f)</math> |
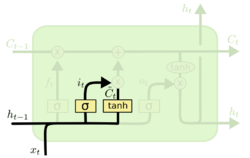
Второй слой вычисляет, насколько ему интересна новая информация, пришедшая с сигналом {{---}} такой же множитель, но уже для наблюдения. | Второй слой вычисляет, насколько ему интересна новая информация, пришедшая с сигналом {{---}} такой же множитель, но уже для наблюдения. | ||
[[File:LSTM_F2.png|none|250px]] | [[File:LSTM_F2.png|none|250px]] | ||
| − | <math>i_t = \sigma(W_f * [ | + | <math>i_t = \sigma(W_f * [h_{t-1}, x_t] + b_i)</math> |
| − | <math>\tilde{C}_t = tanh(W_C * [ | + | <math>\tilde{C}_t = tanh(W_C * [h_{t-1}, x_t] + b_C)</math> |
На третьем слое вычисляется линейная комбинация памяти и наблюдения с только вычисленными весами для каждой из компонент. Так получается новое состояние памяти, которое в таком же виде передаётся далее. | На третьем слое вычисляется линейная комбинация памяти и наблюдения с только вычисленными весами для каждой из компонент. Так получается новое состояние памяти, которое в таком же виде передаётся далее. | ||
[[File:LSTM_F3.png|none|250px]] | [[File:LSTM_F3.png|none|250px]] | ||
| − | <math>C_t = f_t * | + | <math>C_t = f_t * C_{t-1} + i_t * \tilde{C}_t</math> |
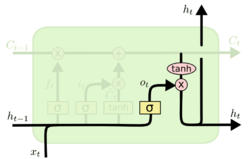
Осталось вычислить output. Но поскольку часть входного сигнала уже в памяти, не нужно считать активацию по всему сигналу. Сначала сигнал проходит через сигмоиду, которая решает, какая его часть важна для дальнейших решений, затем гиперболический тангенс «размазывает» вектор памяти на отрезок от -1 до 1, и в конце эти два вектора перемножаются. | Осталось вычислить output. Но поскольку часть входного сигнала уже в памяти, не нужно считать активацию по всему сигналу. Сначала сигнал проходит через сигмоиду, которая решает, какая его часть важна для дальнейших решений, затем гиперболический тангенс «размазывает» вектор памяти на отрезок от -1 до 1, и в конце эти два вектора перемножаются. | ||
[[File:LSTM_F4.png|none|250px]] | [[File:LSTM_F4.png|none|250px]] | ||
| − | <math>o_t = \sigma(W_o * [ | + | <math>o_t = \sigma(W_o * [h_{t-1}, x_t] + b_o)</math> |
<math>h_t = o_t * tanh(C_t)</math> | <math>h_t = o_t * tanh(C_t)</math> | ||
Версия 05:55, 23 января 2019
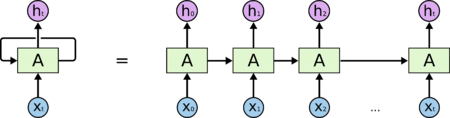
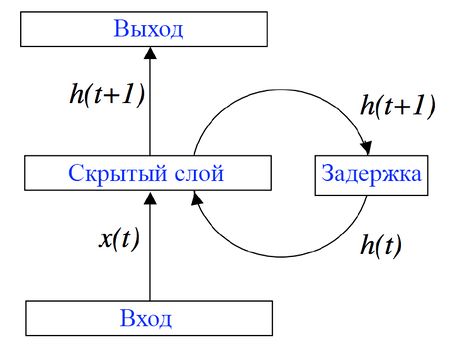
Рекуррентная нейронная сеть (англ. recurrent neural network, RNN) — вид нейронных сетей, где связи между элементами образуют направленную последовательность.
Содержание
Описание
Рекуррентные нейронные сети — сети с циклами, которые хорошо подходят для обработки последовательностей.
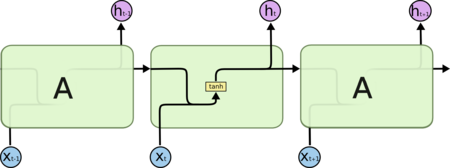
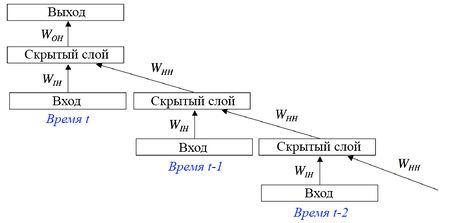
Обучение RNN аналогично обучению обычной нейронной сети. Мы также используем алгоритм обратного распространения ошибки (backpropagation), но с небольшим изменением. Поскольку одни и те же параметры используются на всех временных этапах в сети, градиент на каждом выходе зависит не только от расчетов текущего шага, но и от предыдущих временных шагов. Например, чтобы вычислить градиент при t = 4, нам нужно было бы «распространить ошибку» на 3 шага и суммировать градиенты. Этот алгоритм называется «алгоритмом обратного распространения ошибки сквозь время» (англ. Backpropagation Through Time, BPTT).[1][2]
Области и примеры применения
Используются, когда важно соблюдать последовательность, когда нужен порядок того, что у нас происходит.
- Обработка текста на естественном языке
- Анализ текста
- Автоматический перевод
- Обработка аудио
- Автоматическое распознавание речи
- Обработка видео
- Прогнозирование следующего кадра на основе предыдущих
- Распознавание эмоций
- Обработка изображений
- Прогнозирование следующего пикселя на основе окружения
- Генерация описания изображений
Архитектуры
Полностью рекуррентная сеть
Это базовая архитектура, разработанная в 1980-х. Сеть строится из узлов, каждый из которых соединён со всеми другими узлами. У каждого нейрона порог активации меняется со временем и является вещественным числом. Каждое соединение имеет переменный вещественный вес. Узлы разделяются на входные, выходные и скрытые.
Рекурсивная сеть
Рекурсивные нейронные сети представляют собой более общий случай рекуррентных сетей, когда сигнал в сети проходит через структуру в виде дерева (обычно бинарные деревья). Те же самые матрицы весов используются рекурсивно по всему графу в соответствии с его топологией.
Нейронная сеть Хопфилда
Тип рекуррентной сети, когда все соединения симметричны. Изобретена Джоном Хопфилдом в 1982 году и гарантируется, что динамика такой сети сходится к одному из положений равновесия.
Двунаправленная ассоциативная память (BAM)
Вариацией сети Хопфилда является двунаправленная ассоциативная память (BAM). BAM имеет два слоя, каждый из которых может выступать в качестве входного, находить (вспоминать) ассоциацию и генерировать результат для другого слоя.
Сеть Элмана
Нейронная сеть Элмана состоит из трёх слоев: x, y, z (см рис. Сеть Элмана). Дополнительно к сети добавлен набор «контекстных блоков»: u (см рис. Сеть Элмана). Средний (скрытый) слой соединён с контекстными блоками с фиксированным весом, равным единице. С каждым шагом времени на вход поступает информация, которая проходит прямой ход к выходному слою в соответствии с правилами обучения. Фиксированные обратные связи сохраняют предыдущие значения скрытого слоя в контекстных блоках (до того как скрытый слой поменяет значение в процессе обучения). Таким способом сеть сохраняет своё состояние, что может использоваться в предсказании последовательностей, выходя за пределы мощности многослойного перцептрона.
Обозначения переменных и функций:
- : вектор входного слоя
- : вектор скрытого слоя
- : вектор выходного слоя
- : матрица и вектор параметров
- : функция активации
Сеть Джордана
Нейронная сеть Джордана подобна сети Элмана, но контекстные блоки связаны не со скрытым слоем, а с выходным слоем. Контекстные блоки таким образом сохраняют своё состояние. Они обладают рекуррентной связью с собой.
Эхо-сети
Эхо-сеть (англ. Echo State Network, ESN) характеризуется одним скрытым слоем (который называется резервуаром) со случайными редкими связями между нейронами. При этом связи внутри резервуара фиксированы, но связи с выходным слоем подлежат обучению. Состояние резервуара (state) вычисляется через предыдущие состояния резервуара, а также предыдущие состояния входного и выходного сигналов. Так как эхо-сети обладают только одним скрытым слоем, они обладают достаточно низкой вычислительной сложностью.
Нейронный компрессор истории
Нейронный компрессор исторических данных — это блок, позволяющий в сжатом виде хранить существенные исторические особенности процесса, который является своего рода стеком рекуррентной нейронной сети, формируемым в процессе самообучения.
Сети долго-краткосрочной памяти
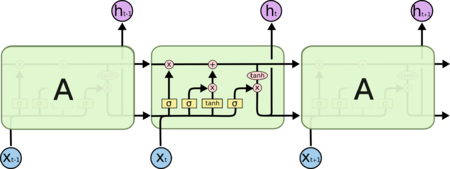
Сеть долго-краткосрочной памяти (англ. Long short-term memory, LSTM) является самой популярная архитектура рекуррентной нейронной сети на данный момент, данная архитектура способна запоминать данные на долгое время.[3]
Разберем работу слоев подробнее[4]:
Первый слой вычисляет, насколько на данном шаге ему нужно забыть предыдущую информацию — по сути множители к компонентам вектора памяти.
Второй слой вычисляет, насколько ему интересна новая информация, пришедшая с сигналом — такой же множитель, но уже для наблюдения.
На третьем слое вычисляется линейная комбинация памяти и наблюдения с только вычисленными весами для каждой из компонент. Так получается новое состояние памяти, которое в таком же виде передаётся далее.
Осталось вычислить output. Но поскольку часть входного сигнала уже в памяти, не нужно считать активацию по всему сигналу. Сначала сигнал проходит через сигмоиду, которая решает, какая его часть важна для дальнейших решений, затем гиперболический тангенс «размазывает» вектор памяти на отрезок от -1 до 1, и в конце эти два вектора перемножаются.
Полученные таким образом и передаются далее по цепочке.
Управляемые рекуррентные блоки
Управляемые рекуррентные блоки (англ. Gated Recurrent Units, GRU) — обладает меньшим количеством параметров, чем у LSTM, и в ней отсутствует выходное управление. При этом производительность в моделях речевого сигнала или полифонической музыки оказалась сопоставимой с LSTM.
Пример кода
Пример кода на Python с использованием библиотеки Keras.[5]
# Импорты
import numpy as np
from keras.preprocessing import sequence
from keras.models import Sequential
from keras.layers import Dense, Activation, Embedding
from keras.layers import LSTM
from keras.datasets import imdb
# Устанавливаем seed для обеспечения повторяемости результатов
np.random.seed(42)
# Указываем количество слов из частотного словаря, которое будет использоваться (отсортированы по частоте использования)
max_features = 5000
# Загружаем данные (датасет IMDB содержит 25000 рецензий на фильмы с правильным ответом для обучения и 25000 рецензий на фильмы с правильным ответом для тестирования)
(X_train, y_train), (X_test, y_test) = imdb.load_data(nb_words = max_features)
# Устанавливаем максимальную длину рецензий в словах, чтобы они все были одной длины
maxlen = 80
# Заполняем короткие рецензии пробелами, а длинные обрезаем
X_train = sequence.pad_sequences(X_train, maxlen = maxlen)
X_test = sequence.pad_sequences(X_test, maxlen = maxlen)
# Создаем модель последовательной сети
model = Sequential()
# Добавляем слой для векторного представления слов (5000 слов, каждое представлено вектором из 32 чисел, отключаем входной сигнал с вероятностью 20% для предотвращения переобучения)
model.add(Embedding(max_features, 32, dropout = 0.2))
# Добавляем слой долго-краткосрочной памяти (100 элементов для долговременного хранения информации, отключаем входной сигнал с вероятностью 20%, отключаем рекуррентный сигнал с вероятностью 20%)
model.add(LSTM(100, dropout_W = 0.2, dropout_U = 0.2))
# Добавляем полносвязный слой из 1 элемента для классификации, в качестве функции активации будем использовать сигмоидальную функцию
model.add(Dense(1, activation = "sigmoid"))
# Компилируем модель нейронной сети
model.compile(loss = 'binary_crossentropy',
optimizer = 'adam',
metrics = ['accuracy'])
# Обучаем нейронную сеть (данные для обучения, ответы к данным для обучения, количество рецензий после анализа которого будут изменены веса, число эпох обучения, тестовые данные, показывать progress bar или нет)
model.fit(X_train, y_train,
batch_size = 64,
nb_epoch = 7,
validation_data = (X_test, y_test),
verbose = 1)
# Проверяем качество обучения на тестовых данных (если есть данные, которые не участвовали в обучении, лучше использовать их, но в нашем случае таковых нет)
scores = model.evaluate(X_test, y_test, batch_size = 64)
print("Точность на тестовых данных: %.2f%%" % (scores[1] * 100))