Метод главных компонент (PCA) — различия между версиями

Материал из Викиконспекты
Перейти к: навигация, поиск
(PCA v0.0.1)
(нет различий)

Версия 04:25, 22 января 2020

Метод главных компонент (англ. Principal Components Analysis, PCA) — один из основных способов уменьшить размерность данных, потеряв наименьшее количество информации. Изобретен К. Пирсоном (англ. Karl Pearson) [1] в 1901 г. Применяется во многих областях, таких как распознавание образов, компьютерное зрение, сжатие данных и т.п. Вычисление главных компонент сводится к вычислению собственных векторов и собственных значений ковариационной матрицы исходных данных или к сингулярному разложению матрицы данных. Иногда метод главных компонент называют преобразованием Кархунена-Лоэва (англ. Karhunen-Loeve) [2] или преобразованием Хотеллинга (англ. Hotelling transform).

Формальная постановка задачи

Иллюстрация к работе К. Пирсона (1901): даны точки [math] P_i[/math] на плоскости, [math] p_i[/math] — расстояние от [math] P_i[/math] до прямой [math] AB[/math]. Ищется прямая [math] AB[/math], минимизирующая сумму [math]\sum_i p_i^2[/math]

Пусть имеется $n$ числовых признаков $f_j(x), j = 1, ... , n$. Объекты обучающей выборки будем отождествлять с их признаковыми описаниями: $x_i \equiv (f_1(x_i), ..., f_n(x_i)), i = 1, ..., l$. Рассмотрим матрицу $F$, строки которой соответствуют признаковым описаниям обучающих объектов: $$F_{l \times n} = \begin{pmatrix} f_1(x_1) & ... & f_n(x_1)\\ ... & ... & ...\\ f_1(x_l) & ... & f_n(x_l) \end{pmatrix} = \begin{pmatrix} x_1\\ ...\\ x_l \end{pmatrix}.$$

Обозначим через $z_i = (g_1(x_i), ..., g_m(x_i))$ признаковые описания тех же объектов в новом пространстве $Z = \mathbb{R}^{m}$ меньшей размерности, $m < n$:

$$G_{l \times m} = \begin{pmatrix} g_1(x_1) & ... & g_m(x_1)\\ ... & ... & ...\\ g_1(x_l) & ... & g_m(x_l) \end{pmatrix} = \begin{pmatrix} z_1\\ ...\\ z_l \end{pmatrix}.$$

Потребуем, чтобы исходные признаковые описания можно было восстановить по новым описаниям с помощью некоторого линейного преобразования, определяемого матрицей $U = (u_{js})_{n \times m}$:

$$\hat{f}_j(x) = \sum_{s = 1}^{m} g_s(x)u_{js}, \; j = 1, ..., n, \; x \in X,$$

или в векторной записи: $\hat{x} = z U^T$. Восстановленное описание $\hat{x}$ не обязано в точности совпадать с исходным описанием $x$, но их отличие на объектах обучающей выборки должно быть как можно меньше при выбранной размерности $m$. Будем искать одновременно и матрицу новых признаковых описаний $G$, и матрицу линейного преобразования $U$, при которых суммарная невязка восстановленных описаний минимальна:

$$\Delta^2(G, U) = \sum_{i = 1}^{l} \| \hat{x}_i - x_i \|^2 = \sum_{i = 1}^{l} \| z_i U^T - x_i \|^2 = \| GU^T - F \|^2 \to \mathop{min}_{G, U},$$

где все нормы евклидовы.

Будем предполагать, что матрицы $G$ и $U$ невырождены: $rank \, G = rank \, U = m$. Иначе существовало бы представление $\bar{G} \bar{U}^T = G U^T$ с числом столбцов в матрице $\bar{G}$, меньшим $m$. Поэтому интересны лишь случаи, когда $m \leq rank \, F$.

Решение

Исчерпывающее решение сформулированной задачи даёт следующая теорема.

Теорема:
Если $m \leq rank \, F$, то минимум $\Delta^2(G, U)$ достигается, когда столбцы матрицы $U$ есть собственные векторы $F^T F$, соответствующие $m$ максимальным собственным значениям. При этом $G = F U$, матрицы $U$ и $G$ ортогональны.
Доказательство:
[math]\triangleright[/math]

Запишем необходимые условия минимума:

[math] \frac{\partial \Delta^2}{\partial G} = (G U^T - F) U = 0;\\ \frac{\partial \Delta^2}{\partial U} = G^T (G U^T - F) = 0. [/math]

Поскольку искомые матрицы $G$ и $U$ невырождены, отсюда следует:

[math] G = F U (U^T U)^{-1};\\ U = F^T G (G^T G)^{-1}. [/math]

Функционал $\Delta^2(G, U)$ зависит только от произведения матриц $G U^T$, поэтому решение задачи $\Delta^2(G, U) \to \mathop{min}_{G, U}$ определено с точностью до произвольного невырожденного преобразования $R: G U^T = (G R) (R^{-1} U^T)$. Распорядимся свободой выбора $R$ так, чтобы матрицы $U^T U$ и $G^T G$ оказались диагональными. Покажем, что это всегда возможно.

Пусть $\tilde{G} \tilde{U}^T$ - произвольное решение задачи.

Матрица $\tilde{U}^T \tilde{U}$ симметричная, невырожденная, положительно определенная, поэтому существует невырожденная матрица $S_{m \times m}$ такая, что $S^{-1} \tilde{U}^T \tilde{U} (S^{-1})^T = I_m$.

Матрица $S^T \tilde{G}^T \tilde{G} S$ симметричная и невырожденная, поэтому существует ортогональная матрица $T_{m \times m}$ такая, что $T^T (S^T \tilde{G}^T \tilde{G} S) T = diag(\lambda_1, ..., \lambda_m) \equiv \Lambda$ - диагональная матрица. По определению ортогональности $T^T T = I_m$.

Преобразование $R = S T$ невырождено. Положим $G = \tilde{G} R$, $U^T = R^{-1} \tilde{U}^T$. Тогда

[math] G^T G = T^T (S^T \tilde{G}^T \tilde{G} S) T = \Lambda;\\ U^T U = T^{-1} (S^{-1} \tilde{U}^T \tilde{U} (S^{-1})^T) (T^{-1})^T = (T^T T)^{-1} = I_m. [/math]

В силу $G U^T = \tilde{G} \tilde{U}^T$ матрицы $G$ и $U$ являются решением задачи $\Delta^2(G, U) \to \mathop{min}_{G, U}$ и удовлетворяют необходимому условию минимума. Подставим матрицы $G$ и $U$ в

[math] G = F U (U^T U)^{-1};\\ U = F^T G (G^T G)^{-1}. [/math]

Благодаря диагональности $G^T G$ и $U^T U$ соотношения существенно упростятся:

[math] G = F U;\\ U \Lambda = F^T G. [/math]

Подставим первое соотношение во второе, получим $U \Lambda = F^T F U$. Это означает, что столбцы матрицы $U$ обязаны быть собственными векторами матрицы $F^T F$, а диагональные элементы $\lambda_1, ..., \lambda_m$ - соответствующими им собственными значениями.

Аналогично, подставив второе соотношение в первое, получим $G \Lambda = F F^T G$, то есть столбцы матрицы $G$ являются собственными векторами $F F^T$, соответствующими тем же самым собственным значениям.

Подставляя $G$ и $U$ в функционал $\Delta^2(G, U)$, находим:

[math] \Delta^2(G, U) = \| F - G U^T \|^2 = tr \, (F^T - U G^t)(F - G U^T) = tr \, F^T (F - G U^T) = tr \, F^T F - tr \, F^T G U^T = \| F \|^2 - tr \, U \Lambda U^T = \| F \|^2 - tr \, \Lambda = \sum_{j = 1}^{n} \lambda_j - \sum_{j = 1}^{m} \lambda_j - \sum_{j = m + 1}^{n} \lambda_j, [/math]

где $\lambda_1 , ..., \lambda_n$ - все собственные значения матрицы $F^T F$. Минимум $\Delta^2$ достигается, когда $\lambda_1, ..., \lambda_m$ - наибольшие $m$ из $n$ собственных значений.

Собственные векторы $u_1, ..., u_m$, отвечающие максимальным собственным значениям, называют главными компонентами.
[math]\triangleleft[/math]

Свойства

Связь с сингулярным разложением

Если $m = n$, то $\Delta^2(G, U) = 0$. В этом случае представление $F = G U^T$ является точным и совпадает с сингулярным разложением: $F = G U^T = V D U^T$, если положить $G = V D$ и $\Lambda = D^2$. При этом матрица $V$ ортогональна: $V^T V = I_m$.

Если $m < n$, то то представление $F \approx G U^T$ является приближённым. Сингулярное разложение матрицы $G U^T$ получается из сингулярного разложения матрицы $F$ путём отбрасывания (обнуления) $n - m$ минимальных собственных значений.

Преобразование Карунена–Лоэва

Диагональность матрицы $G^T G = \Lambda$ означает, что новые признаки $g_1, ..., g_m$ не коррелируют на обучающих объектах. Ортогональное преобразование $U$ называют декоррелирующим или преобразованием Карунена– Лоэва. Если $m = n$, то о прямое и обратное преобразование вычисляются с помощью одной и той же матрицы $U: F = G U^T$ и $G = F U$.

Эффективная размерность

Главные компоненты содержат основную информацию о матрице $F$. Число главных компонент $m$ называют также эффективной размерностью задачи. На практике её определяют следующим образом. Все собственные значения матрицы $F^T F$ упорядочиваются по убыванию: $\lambda_1 \geq ... \geq \lambda_n \geq 0$. Задаётся пороговое значение $\epsilon \in [0, 1]$, достаточно близкое к нулю, и определяется наименьшее целое $m$, при котором относительная погрешность приближения матрицы $F$ не превышает $\epsilon$:

$$E(m) = \frac{\| G U^T - F \|^2}{\| F \|^2} = \frac{\lambda_{m + 1} + ... + \lambda_n}{\lambda_1 + ... + \lambda_n} \leq \epsilon .$$

Величина $E(m)$ показывает, какая доля информации теряется при замене исходных признаковых описаний длины $n$ на более короткие описания длины $m$. Метод главных компонент особенно эффективен в тех случаях, когда $E(m)$ оказывается малым уже при малых значениях $m$. Если задать число $\epsilon$ из априорных соображений не представляется возможным, прибегают к критерию «крутого обрыва». На графике $E(m)$ отмечается то значение $m$, при котором происходит резкий скачок: $E(m - 1) \gg E(m)$, при условии, что $E(m)$ уже достаточно мало.

Визуализация многомерных данных

Метод главных компонент часто используется для представления многомерной выборки данных на двумерном графике. Для этого полагают $m = 2$ и полученные пары значений $(g_1(x_i), g_2(x_i)), i = 1, ..., l$, наносят как точки на график. Проекция на главные компоненты является наименее искаженной из всех линейных проекций многомерной выборки на какую-либо пару осей. Как правило, в осях главных компонент удаётся увидеть наиболее существенные особенности исходных данных, даже несмотря на неизбежные искажения. В частности, можно судить о наличии кластерных структур и выбросов. Две оси $g_1$ и $g_2$ отражают «две основные тенденции» в данных. Иногда их удаётся интерпретировать, если внимательно изучить, какие точки на графике являются «самыми левыми», «самыми правыми», «самыми верхними» и «самыми нижними». Этот вид анализа не позволяет делать точные количественные выводы и обычно используется с целью понимания данных. Аналогичную роль играют многомерное шкалирование [3] и карты Кохонена [4].

Пример кода scikit-learn

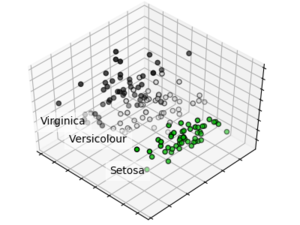
Пример применения PCA к датасету Iris для уменьшения размерности: 

 # Импорт библиотек
 import numpy as np
 import matplotlib.pyplot as plt
 from mpl_toolkits.mplot3d import Axes3D
 from sklearn import decomposition
 from sklearn import datasets

 # Загрузка данных
 centers = [[1, 1], [-1, -1], [1, -1]]
 iris = datasets.load_iris()
 X = iris.data
 y = iris.target

 # Инициализация графика
 fig = plt.figure(1, figsize=(4, 3))
 plt.clf()
 ax = Axes3D(fig, rect=[0, 0, .95, 1], elev=48, azim=134)
 plt.cla()

 # Преобразование данных датасета Iris, уменьшающее размерность до 3
 pca = decomposition.PCA(n_components=3)
 pca.fit(X)
 X = pca.transform(X)
Применения PCA к датасету Iris
 # Отображение меток и преобразованных данных на графике
 for name, label in [('Setosa', 0), ('Versicolour', 1), ('Virginica', 2)]:
     ax.text3D(X[y == label, 0].mean(),
               X[y == label, 1].mean() + 1.5,
               X[y == label, 2].mean(), name,
               horizontalalignment='center',
               bbox=dict(alpha=.5, edgecolor='w', facecolor='w'))
 y = np.choose(y, [1, 2, 0]).astype(np.float)
 ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=y, cmap=plt.cm.nipy_spectral,
            edgecolor='k')
 ax.w_xaxis.set_ticklabels([])
 ax.w_yaxis.set_ticklabels([])
 ax.w_zaxis.set_ticklabels([])
 plt.show()

См. также

Примечания

  1. ↑ Pearson, K. (1901). "On Lines and Planes of Closest Fit to Systems of Points in Space"
  2. ↑ Karhunen-Loeve Transform (KLT)
  3. ↑ Многомерное шкалирование
  4. ↑ Самоорганизующаяся карта Кохонена

Источники информации

  1. machinelearning.ru — Метод главных компонент
  2. Лекция "Регрессионный анализ и метод главных компонентов" — К.В. Воронцов, курс "Машинное обучение" 2014
  3. PCA — курс ML Texas A&M University
  4. Principal Component Analysis — статья про Principal Component Analysis в Wikipedia
  5. Understanding PCA
Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Метод_главных_компонент_(PCA)&oldid=72328»