Метод главных компонент (PCA)
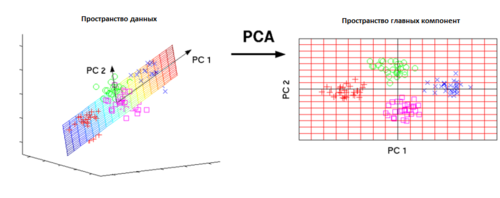
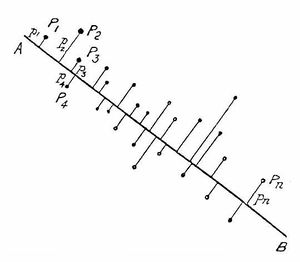
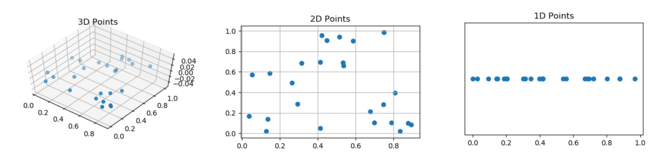
Метод главных компонент (англ. Principal Components Analysis, PCA) — один из основных способов уменьшить размерность данных, потеряв наименьшее количество информации. Изобретен К. Пирсоном (англ. Karl Pearson) [1] в 1901 г. Применяется во многих областях, таких как распознавание образов, компьютерное зрение, сжатие данных и т.п. Вычисление главных компонент сводится к вычислению собственных векторов и собственных значений ковариационной матрицы исходных данных или к сингулярному разложению матрицы данных. Иногда метод главных компонент называют преобразованием Карунена-Лоэва (англ. Karhunen-Loeve) [2] или преобразованием Хотеллинга (англ. Hotelling transform).
Формальная постановка задачи
Пусть имеется $n$ числовых признаков $f_j(x), j = 1, ... , n$. Объекты обучающей выборки будем отождествлять с их признаковыми описаниями: $x_i \equiv (f_1(x_i), ..., f_n(x_i)), i = 1, ..., l$. Рассмотрим матрицу $F$, строки которой соответствуют признаковым описаниям обучающих объектов: $$F_{l \times n} = \begin{pmatrix} f_1(x_1) & ... & f_n(x_1)\\ ... & ... & ...\\ f_1(x_l) & ... & f_n(x_l) \end{pmatrix} = \begin{pmatrix} x_1\\ ...\\ x_l \end{pmatrix}.$$
Обозначим через $z_i = (g_1(x_i), ..., g_m(x_i))$ признаковые описания тех же объектов в новом пространстве $Z = \mathbb{R}^{m}$ меньшей размерности, $m < n$:
$$G_{l \times m} = \begin{pmatrix} g_1(x_1) & ... & g_m(x_1)\\ ... & ... & ...\\ g_1(x_l) & ... & g_m(x_l) \end{pmatrix} = \begin{pmatrix} z_1\\ ...\\ z_l \end{pmatrix}.$$
Потребуем, чтобы исходные признаковые описания можно было восстановить по новым описаниям с помощью некоторого линейного преобразования, определяемого матрицей $U = (u_{js})_{n \times m}$:
$$\hat{f}_j(x) = \sum_{s = 1}^{m} g_s(x)u_{js}, \; j = 1, ..., n, \; x \in X,$$
или в векторной записи: $\hat{x} = z U^T$. Восстановленное описание $\hat{x}$ не обязано в точности совпадать с исходным описанием $x$, но их отличие на объектах обучающей выборки должно быть как можно меньше при выбранной размерности $m$. Будем искать одновременно и матрицу новых признаковых описаний $G$, и матрицу линейного преобразования $U$, при которых суммарная невязка $\Delta^2(G, U)$ восстановленных описаний минимальна:
$$\Delta^2(G, U) = \sum_{i = 1}^{l} \| \hat{x}_i - x_i \|^2 = \sum_{i = 1}^{l} \| z_i U^T - x_i \|^2 = \| GU^T - F \|^2 \to \mathop{min}_{G, U},$$
где все нормы евклидовы.
Будем предполагать, что матрицы $G$ и $U$ невырождены: $rank \, G = rank \, U = m$. Иначе существовало бы представление $\bar{G} \bar{U}^T = G U^T$ с числом столбцов в матрице $\bar{G}$, меньшим $m$. Поэтому интересны лишь случаи, когда $m \leq rank \, F$.
Решение
Исчерпывающее решение сформулированной задачи даёт следующая теорема.
| Теорема: |
Если , то минимум достигается, когда столбцы матрицы есть собственные векторы , соответствующие максимальным собственным значениям. При этом , матрицы и ортогональны. |
| Доказательство: |
|
Запишем необходимые условия минимума:
Поскольку искомые матрицы $G$ и $U$ невырождены, отсюда следует:
Функционал $\Delta^2(G, U)$ зависит только от произведения матриц $G U^T$, поэтому решение задачи $\Delta^2(G, U) \to \mathop{min}_{G, U}$ определено с точностью до произвольного невырожденного преобразования $R: G U^T = (G R) (R^{-1} U^T)$. Распорядимся свободой выбора $R$ так, чтобы матрицы $U^T U$ и $G^T G$ оказались диагональными. Покажем, что это всегда возможно. Пусть $\tilde{G} \tilde{U}^T$ — произвольное решение задачи. Матрица $\tilde{U}^T \tilde{U}$ симметричная, невырожденная, положительно определенная, поэтому существует невырожденная матрица $S_{m \times m}$ такая, что $S^{-1} \tilde{U}^T \tilde{U} (S^{-1})^T = I_m$. Матрица $S^T \tilde{G}^T \tilde{G} S$ симметричная и невырожденная, поэтому существует ортогональная матрица $T_{m \times m}$ такая, что $T^T (S^T \tilde{G}^T \tilde{G} S) T = diag(\lambda_1, ..., \lambda_m) \equiv \Lambda$ — диагональная матрица. По определению ортогональности $T^T T = I_m$. Преобразование $R = S T$ невырождено. Положим $G = \tilde{G} R$, $U^T = R^{-1} \tilde{U}^T$. Тогда
В силу $G U^T = \tilde{G} \tilde{U}^T$ матрицы $G$ и $U$ являются решением задачи $\Delta^2(G, U) \to \mathop{min}_{G, U}$ и удовлетворяют необходимому условию минимума. Подставим матрицы $G$ и $U$ в
Благодаря диагональности $G^T G$ и $U^T U$ соотношения существенно упростятся:
Подставим первое соотношение во второе, получим $U \Lambda = F^T F U$. Это означает, что столбцы матрицы $U$ обязаны быть собственными векторами матрицы $F^T F$, а диагональные элементы $\lambda_1, ..., \lambda_m$ - соответствующими им собственными значениями. Аналогично, подставив второе соотношение в первое, получим $G \Lambda = F F^T G$, то есть столбцы матрицы $G$ являются собственными векторами $F F^T$, соответствующими тем же самым собственным значениям. Подставляя $G$ и $U$ в функционал $\Delta^2(G, U)$, находим: = = = = = = = где $\lambda_1 , ..., \lambda_n$ - все собственные значения матрицы $F^T F$. Минимум $\Delta^2$ достигается, когда $\lambda_1, ..., \lambda_m$ — наибольшие $m$ из $n$ собственных значений. Собственные векторы $u_1, ..., u_m$, отвечающие максимальным собственным значениям, называют главными компонентами. |
Свойства
Связь с сингулярным разложением
Если $m = n$, то $\Delta^2(G, U) = 0$. В этом случае представление $F = G U^T$ является точным и совпадает с сингулярным разложением: $F = G U^T = V D U^T$, если положить $G = V D$ и $\Lambda = D^2$. При этом матрица $V$ ортогональна: $V^T V = I_m$.
Если $m < n$, то представление $F \approx G U^T$ является приближённым. Сингулярное разложение матрицы $G U^T$ получается из сингулярного разложения матрицы $F$ путём отбрасывания (обнуления) $n - m$ минимальных собственных значений.
Преобразование Карунена–Лоэва
Диагональность матрицы $G^T G = \Lambda$ означает, что новые признаки $g_1, ..., g_m$ не коррелируют на объектах из обучающей выборки. Ортогональное преобразование $U$ называют декоррелирующим или преобразованием Карунена–Лоэва. Если $m = n$, то о прямое и обратное преобразование вычисляются с помощью одной и той же матрицы $U: F = G U^T$ и $G = F U$.
Эффективная размерность
Главные компоненты содержат основную информацию о матрице $F$. Число главных компонент $m$ называют также эффективной размерностью задачи. На практике её определяют следующим образом. Все собственные значения матрицы $F^T F$ упорядочиваются по убыванию: $\lambda_1 \geq ... \geq \lambda_n \geq 0$. Задаётся пороговое значение $\epsilon \in [0, 1]$, достаточно близкое к нулю, и определяется наименьшее целое $m$, при котором относительная погрешность приближения матрицы $F$ не превышает $\epsilon$:
$$E(m) = \frac{\| G U^T - F \|^2}{\| F \|^2} = \frac{\lambda_{m + 1} + ... + \lambda_n}{\lambda_1 + ... + \lambda_n} \leq \epsilon .$$
Величина $E(m)$ показывает, какая доля информации теряется при замене исходных признаковых описаний длины $n$ на более короткие описания длины $m$. Метод главных компонент особенно эффективен в тех случаях, когда $E(m)$ оказывается малым уже при малых значениях $m$. Если задать число $\epsilon$ из априорных соображений не представляется возможным, прибегают к критерию «крутого обрыва». На графике $E(m)$ отмечается то значение $m$, при котором происходит резкий скачок: $E(m - 1) \gg E(m)$, при условии, что $E(m)$ уже достаточно мало.
Визуализация многомерных данных
Метод главных компонент часто используется для представления многомерной выборки данных на двумерном графике. Для этого полагают $m = 2$ и полученные пары значений $(g_1(x_i), g_2(x_i)), i = 1, ..., l$, наносят как точки на график. Проекция на главные компоненты является наименее искаженной из всех линейных проекций многомерной выборки на какую-либо пару осей. Как правило, в осях главных компонент удаётся увидеть наиболее существенные особенности исходных данных, даже несмотря на неизбежные искажения. В частности, можно судить о наличии кластерных структур и выбросов. Две оси $g_1$ и $g_2$ отражают «две основные тенденции» в данных. Иногда их удаётся интерпретировать, если внимательно изучить, какие точки на графике являются «самыми левыми», «самыми правыми», «самыми верхними» и «самыми нижними». Этот вид анализа не позволяет делать точные количественные выводы и обычно используется с целью понимания данных. Аналогичную роль играют многомерное шкалирование [3] и карты Кохонена [4].
Пределы применимости и ограничения эффективности метода
Метод главных компонент применим всегда. Распространённое утверждение о том, что он применим только к нормально распределённым данным (или для распределений, близких к нормальным) неверно: в исходной формулировке К. Пирсона ставится задача об аппроксимации конечного множества данных и отсутствует даже гипотеза о их статистическом порождении, не говоря уж о распределении.
Однако метод не всегда эффективно снижает размерность при заданных ограничениях на точность $E(m)$. Прямые и плоскости не всегда обеспечивают хорошую аппроксимацию. Например, данные могут с хорошей точностью следовать какой-нибудь кривой, а эта кривая может быть сложно расположена в пространстве данных. В этом случае метод главных компонент для приемлемой точности потребует нескольких компонент (вместо одной), или вообще не даст снижения размерности при приемлемой точности.
Больше неприятностей могут доставить данные сложной топологии. Для их аппроксимации также изобретены различные методы, например самоорганизующиеся карты Кохонена [4] или нейронный газ [5]. Если данные статистически порождены с распределением, сильно отличающимся от нормального, то для аппроксимации распределения полезно перейти от главных компонент к независимым компонентам [6], которые уже не ортогональны в исходном скалярном произведении. Наконец, для изотропного распределения (даже нормального) вместо эллипсоида рассеяния получаем шар, и уменьшить размерность методами аппроксимации невозможно.
Примеры кода
Пример кода scikit-learn
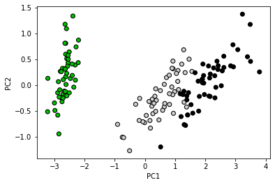
Пример применения PCA к датасету Iris для уменьшения размерности:
# Импорт библиотек
import numpy as np
import matplotlib.pyplot as plt
from sklearn import decomposition
from sklearn import datasets
# Загрузка данных
centers = [[1, 1], [-1, -1], [1, -1]]
iris = datasets.load_iris()
X = iris.data
y = iris.target
# Преобразование данных датасета Iris, уменьшающее размерность до 2
pca = decomposition.PCA(n_components=3)
pca.fit(X)
X = pca.transform(X)
y = np.choose(y, [1, 2, 0]).astype(np.float)
plt.clf()
plt.cla()
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.nipy_spectral, edgecolor='k')
plt.xlabel("PC1")
plt.ylabel("PC2")
plt.show()
Пример на языке R
# importing library and its' dependencies
library(h2o)
h2o.init()
path <- system.file("extdata", "data.csv", package = "h2o")
data <- h2o.uploadFile(path = data)
# evaluating
h2o.prcomp(training_frame = data, k = 8, transform = "STANDARDIZE")
См. также
Примечания
Источники информации
- machinelearning.ru — Метод главных компонент
- Лекция "Регрессионный анализ и метод главных компонентов" — К.В. Воронцов, курс "Машинное обучение" 2014
- PCA — курс ML Texas A&M University
- Principal Component Analysis — статья про Principal Component Analysis в Wikipedia
- Understanding PCA