Вершинная, рёберная связность, связь между ними и минимальной степенью вершины

Определения

Определение:

Вершинной связностью [math]\varkappa[/math] графа [math]G[/math] называется наименьшее число вершин, удаление которых приводит к несвязному или тривиальному графу.

Определение:

Реберной связностью [math]\lambda[/math] графа [math]G[/math] называется наименьшее количество ребер, удаление которых приводит к несвязному или тривиальному графу.

Связь между [math]\varkappa[/math], [math]\lambda[/math] и минимальной степенью вершины

Пускай минимальная степень вершины графа [math]G[/math] обозначается буквой [math]\delta[/math]. Тогда:

Теорема:

Для любого графа [math]G[/math] справедливо следующее неравенство: [math]\varkappa \le\lambda \le \delta [/math]

Доказательство:

[math]\triangleright[/math]

Полный граф. [math] \lambda = \delta = \varkappa = 4[/math] 1) Проверим второе неравенство. Если в графе [math]G[/math] нет ребер, то [math] \lambda = 0 [/math]. Если ребра есть, то несвязный граф получаем из данного, удаляя все ребра, инцидентные вершине с наименьшей степенью. В любом случае [math] \lambda \le \delta [/math]. 2) Чтобы проверить первое неравенство нужно рассмотреть несколько случаев. Если [math]G[/math] - несвязный или тривиальный граф, то [math] \varkappa = \lambda = 0 [/math]. Если [math]G[/math] связен и имеет мост [math]x[/math], то [math]\lambda = 1 [/math]. В последнем случае [math] \varkappa = 1 [/math], поскольку или граф [math]G[/math] имеет точку сочленения, инцидентную ребру [math]x[/math], или же [math]G=K_2[/math]. Наконец, предположим, что граф [math]G[/math] содержит множество из [math] \lambda \ge 2 [/math] ребер, удаление которых делает его несвязным. Ясно, что удаляя [math]\lambda - 1 [/math] ребер из этого множества получаем граф, имеющий мост [math]x = uv[/math]. Для каждого из этих [math]\lambda - 1 [/math] ребер выберем какую-либо инцидентную с ним вершину отличную от [math]u[/math] и [math]v[/math]. Удаление выбранных вершин приводит к удалению [math]\lambda - 1 [/math] (а возможно, и большего числа) ребер. Если получаемый после такого удаления граф не связен, то [math]\varkappa \lt \lambda[/math]; если же он связен, то в нем есть мост [math]x[/math], и поэтому удаление вершины [math]u[/math] или [math]v[/math] приводит либок несвязному, либо к тривиальному графу. в любом случае [math] \varkappa \le \lambda[/math].

[math]\triangleleft[/math]

Теорема:

Для любых натуральных чисел [math]a, b, c[/math], таких что [math]a \le b \le c[/math], существует граф [math]G[/math], у которого [math]\varkappa = a, \lambda = b[/math] и [math]\delta = c [/math]

Доказательство:

[math]\triangleright[/math]

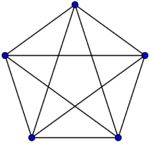
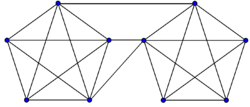
Граф, в котором [math] \delta = 4[/math], [math]\lambda = 3[/math], [math]\varkappa = 2[/math]. Рассмотрим граф [math]G[/math], являющийся объединением двух полных графов [math]G_1[/math] и [math]G_2[/math], содержащих [math]c + 1[/math] вершину. Отметим [math]b[/math] вершин, принадлежащих подграфу [math]G_1[/math] и [math]a[/math] вершин, принадлежащих подграфу [math]G_2[/math]. Добавим в граф [math]G[/math] [math]b[/math] ребер так, чтобы каждое ребро было инцидентно помеченной вершине, лежащей в подграфе [math]G_1[/math] и помеченной вершине, лежащей в подграфе [math]G_2[/math], причем не осталось ни одной помеченной вершины, у которой не появилось хотя бы одно новое ребро, инцидентное ей. Тогда: 1) Поскольку [math]b \le c[/math], то было как минимум две непомеченные вершины, поэтому [math] \delta = c[/math], так как минимальные степени вершин графов [math]G_1[/math] и [math]G_2[/math] были равны [math]c[/math], а степени их вершин не уменьшались. 2) Заметим, что между двумя вершинами графа [math]G[/math] существует не меньше [math]a[/math] вершинно-непересекающихся простых цепей, следовательно по теореме Менгера [math]\varkappa \ge a[/math]. Однако если удалить из графа [math]G[/math] помеченные вершины его подграфа [math]G_2[/math], то граф [math]G[/math] потеряет связность. Значит, [math]\varkappa = a[/math]. 3) Аналогично рассуждению пункта 2, легко убедится, что [math]\lambda = b[/math].

[math]\triangleleft[/math]

Литература

• Харари Ф. Теория графов: Пер. с англ. / Предисл. В. П. Козырева; Под ред. Г.П.Гаврилова. Изд. 4-е. — М.: Книжный дом "ЛИБРОКОМ", 2009. — 60 с.