Сиамская нейронная сеть — различия между версиями

Материал из Викиконспекты
Перейти к: навигация, поиск
(Исправлены опечатки и добавлена категория)
(Исправлена функция)
Строка 23: Строка 23:
 
где <math>\tau</math> — это заранее заданный предел. Вторая функция потерь — triplet loss function — требует объект рассматриваемого класса (или якорь, англ. anchor) <math>h_i</math>, с которым будет проводиться сравнение, а также два других объекта: один принадлежащий к тому же классу (англ. neighbor) <math>h_j</math>, и один не принадлежащий к этому классу (англ. distant) <math>h_k</math>:
 
где <math>\tau</math> — это заранее заданный предел. Вторая функция потерь — triplet loss function — требует объект рассматриваемого класса (или якорь, англ. anchor) <math>h_i</math>, с которым будет проводиться сравнение, а также два других объекта: один принадлежащий к тому же классу (англ. neighbor) <math>h_j</math>, и один не принадлежащий к этому классу (англ. distant) <math>h_k</math>:
  
−
<math>l(x_i, x_j, z_{ij}) = \max(0, ||h_i-h_j||_2^2 - ||h_i-h_k||_2^2 + \alpha)</math>,
+
<math>l(x_i, x_j, x_k) = \max(0, ||h_i-h_j||_2^2 - ||h_i-h_k||_2^2 + \alpha)</math>,
  
 
где <math>\alpha</math> — это заранее заданный предел. Обе функции стремятся приблизить похожие объекты, и увеличить расстояние между разными объектами. В некоторых случаях, возможно их совместное применение для достижения наилучшего результата<ref name="both">X. Di and V. M. Patel. Deep tattoo recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, pages 51–58, 2016.</ref>. Тогда [[Функция потерь и эмпирический риск|эмпирический риск]] (англ. error function) равен
 
где <math>\alpha</math> — это заранее заданный предел. Обе функции стремятся приблизить похожие объекты, и увеличить расстояние между разными объектами. В некоторых случаях, возможно их совместное применение для достижения наилучшего результата<ref name="both">X. Di and V. M. Patel. Deep tattoo recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, pages 51–58, 2016.</ref>. Тогда [[Функция потерь и эмпирический риск|эмпирический риск]] (англ. error function) равен
  
−
<math>L(W) = \sum_{i,j} l(x_i, x_j, z_{ij}) + \mu R(W)</math>,
+
<math>L(W) = \sum l + \mu R(W)</math>,
  
 
где <math>R(W)</math> — это член, регуляризующий обобщающую способность сети, <math>W</math> — это матрица параметров нейронных подсетей, а <math>\mu</math> — это гиперпараметр, отвечающий за степень регуляризации. Для минимизации этой функции обычно применяется [[Стохастический градиентный спуск|градиентный спуск]] (англ. gradient descent).
 
где <math>R(W)</math> — это член, регуляризующий обобщающую способность сети, <math>W</math> — это матрица параметров нейронных подсетей, а <math>\mu</math> — это гиперпараметр, отвечающий за степень регуляризации. Для минимизации этой функции обычно применяется [[Стохастический градиентный спуск|градиентный спуск]] (англ. gradient descent).

Версия 21:41, 27 декабря 2020

Сиамская нейронная сеть (англ. Siamese neural network) — это разновидность искусственной нейронной сети (англ. neural network), которая состоит из двух идентичных нейронных подсетей с одинаковыми наборами весов. Данный вид сетей позволяет сравнить вектора признаков двух объектов с целью выделить их семантическое сходство или различие. Сиамская нейронная сеть представляет собой нелинейное отображение данных с целью приблизить друг к другу схожие объекты и разнести на максимально возможное расстояние различные объекты. Сиамские сети получили свое название от сиамских близнецов, физически приросших друг к другу, из-за использования сразу двух подсетей, разделяющих один набор весов. Эти подсети могут быть представлены многослойными перцептронами (англ. multilayer perceptron), сверточными нейронными сетями (англ. convolutional neural network) и другими.

Сиамская нейронная сеть

Рисунок 1 — обобщенная архитектура сиамской нейронной сети.
Рисунок 2 — основные типы архитектур сиамской нейронной сети.

Зададимся набором данных [math]\{(x_i, y_i), i = 1, \dots, n\}[/math], состоящим из [math]n[/math] векторов признаков [math]x_i \in R^m[/math] размера [math]m[/math] с метками [math]y_i \in \{1, 2, \dots, C\}[/math]. Создадим обучающий набор данных [math]S = \{(x_i, x_j, z_{ij}), (i,j) \in K\}[/math], состоящих из пар [math]x_i[/math] и [math]x_j[/math] с бинарными метками [math]z_{ij}[/math]. Если оба вектора признаков [math]x_i[/math] и [math]x_j[/math] принадлежат к одному и тому же классу, то [math]z_{ij} = 0[/math], иначе [math]z_{ij} = 1[/math]. Разделим обучающий набор данных [math]S[/math] на два подмножества: одно — со схожими парами (или с [math]z_{ij} = 0[/math]), другое — с различающимися парами (или с [math]z_{ij} = 1[/math]). Будем подавать наши пары векторов на вход сиамской подсети.

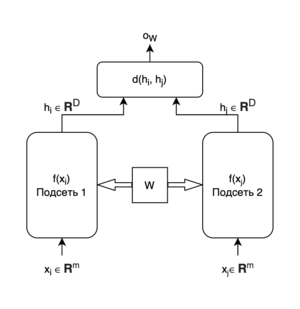
В общем случае сиамская сеть состоит из двух подсетей, выходы которых подаются на вход другого модуля, который генерирует конечный выход. Рассмотрим Рис. 1, на котором [math]x_i[/math] и [math]x_j[/math] — это входы, [math]W[/math] — общие веса/параметры, а [math]h_i \in R^D[/math] и [math]h_j \in R^D[/math] — выходы обеих подсетей. Сиамская сеть представляет собой отображение [math]h_i = f(x_i)[/math], для которого Евклидово расстояние [math]d(h_i, h_j)[/math] максимально мало́ при [math]y_i=y_j[/math] и максимально велико при [math]y_i \neq y_j[/math]. Сеть возвращает оценку [math]o_W[/math] того, насколько различны [math]x_i[/math] и [math]x_j[/math].

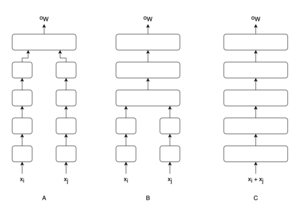
Существует три главных вида структуры сиамских нейронных сетей (см. Рис. 2):

  1. Входы [math]x_i[/math] и [math]x_j[/math] подаются на две параллельные подсети, представляющие собой две отдельные сети с одними и теми же весами и смещениями. Для выходов [math]h_i[/math] и [math]h_j[/math] этих сетей подсчитывается метрика расстояния [math]d(h_i, h_j)[/math], которая подается на выходной слой, оценивающий схожесть [math]o_W[/math] между входами подсетей.
  2. Несколько последних слоев подсетей объединены, за ними следуют несколько дополнительных слоев. На последнем слое применяется softmax-преобразование. Данная архитектура известна под названием In-network stacking.
  3. Оба входа [math]x_i[/math] и [math]x_j[/math] конкатенируются и подаются на вход единой сети, завершающейся слоем с softmax-преобразованием.

Третья архитектура полезна для детального сравнения двух объектов, необходимого, например, при отслеживании пешеходов[1]. Первые две архитектуры показывают хорошие результаты при классификации.

Существует много различных функций потерь (англ. loss function) для обучения сиамских нейронных сетей. Рассмотрим две наиболее популярные из них. Первая — contrastive loss function — использует пары объектов [math]x_i, x_j[/math], которые могут принадлежать как одному, так и разным классам:

[math]l(x_i, x_j, z_{ij}) = (1-z_{ij})||h_i-h_j||_2^2+z_{ij}\max(0, \tau-||h_i-h_j||_2^2)[/math],

где [math]\tau[/math] — это заранее заданный предел. Вторая функция потерь — triplet loss function — требует объект рассматриваемого класса (или якорь, англ. anchor) [math]h_i[/math], с которым будет проводиться сравнение, а также два других объекта: один принадлежащий к тому же классу (англ. neighbor) [math]h_j[/math], и один не принадлежащий к этому классу (англ. distant) [math]h_k[/math]:

[math]l(x_i, x_j, x_k) = \max(0, ||h_i-h_j||_2^2 - ||h_i-h_k||_2^2 + \alpha)[/math],

где [math]\alpha[/math] — это заранее заданный предел. Обе функции стремятся приблизить похожие объекты, и увеличить расстояние между разными объектами. В некоторых случаях, возможно их совместное применение для достижения наилучшего результата[2]. Тогда эмпирический риск (англ. error function) равен

[math]L(W) = \sum l + \mu R(W)[/math],

где [math]R(W)[/math] — это член, регуляризующий обобщающую способность сети, [math]W[/math] — это матрица параметров нейронных подсетей, а [math]\mu[/math] — это гиперпараметр, отвечающий за степень регуляризации. Для минимизации этой функции обычно применяется градиентный спуск (англ. gradient descent).

Сеть триплетов

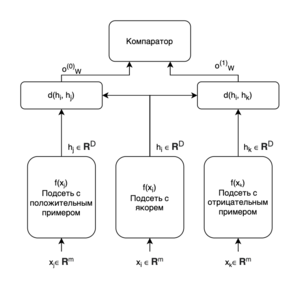
Рисунок 3 — обобщенная архитектура сети триплетов.

Сеть триплетов (англ. Triplet network) (см. Рис. 3) представляет собой модификацию сиамской сети с тремя сверточными нейронными подсетями с общими параметрами. В центральную подсеть подается объект [math]x_i[/math] класса [math]y[/math], принадлежность к которому мы хотим научиться определять. В одну из двух оставшихся подсетей подается объект [math]x_j[/math] того же класса [math]y[/math] (положительный пример), а в другую — объект [math]x_k[/math], не принадлежащий к классу [math]y[/math] (негативный пример). Сочетание центральной подсети с каждой из двух других подсетей образует сиамскую сеть. Выходы [math]o_W^{(0)}[/math] и [math]o_W^{(1)}[/math] обеих сиамских сетей подаются на последний слой-компаратор. Было отмечено, что при обучении сети триплетов в качестве функции потерь удобнее использовать среднеквадратическую ошибку[3].

Как сиамская сеть, так и сеть триплетов показывают хорошие результаты при сравнении изображений. Однако, в отличие от сиамской сети, сеть триплетов не требует нормализации данных.

Применение

Сиамские нейронные сети нашли широкое применение в области компьютерного зрения, распознавания речи и обработки естественных языков. Были предложены модели для распознавания манеры ходьбы[4], поведения пользователя в интернете[5], множественного трекинга пешеходов[1], и т.д.[6][7][8] Данный вид сетей также может быть использован для снижения размерности.

Однако наиболее популярное применение сиамский сетей — это распознавание лиц. Первые автоматизированные решения в этой области появились еще в 1960-е годы. Однако свою популярность распознание лиц приобрело после публикации метода eigenface[9], использующем алгоритмы снижения размерности (например, PCA) для компактного представления признаков. Позже, данное решение было улучшено с помощью применения сверточных нейронных сетей. Сиамские нейронные сети являются усовершенствованием над нейронными сетями и часто используются в задачах, когда фактическое число классов велико или не известно во время обучения, а количество объектов в классах мало.

См. также

Примечания

  1. ↑ 1,0 1,1 L. Leal-Taixé, C. Canton-Ferrer and K. Schindler, "Learning by Tracking: Siamese CNN for Robust Target Association," 2016 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Las Vegas, NV, 2016, pp. 418-425, doi: 10.1109/CVPRW.2016.59.
  2. ↑ X. Di and V. M. Patel. Deep tattoo recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, pages 51–58, 2016.
  3. ↑ Elad Hoffer, Nir Ailon, "Deep metric learning using Triplet network", 2018.[1]
  4. ↑ C. Zhang, W. Liu, H. Ma and H. Fu, "Siamese neural network based gait recognition for human identification," 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, 2016, pp. 2832-2836, doi: 10.1109/ICASSP.2016.7472194.
  5. ↑ Y. Qiao, Y. Wu, F. Duo, W. Lin and J. Yang, "Siamese Neural Networks for User Identity Linkage Through Web Browsing," in IEEE Transactions on Neural Networks and Learning Systems, vol. 31, no. 8, pp. 2741-2751, Aug. 2020, doi: 10.1109/TNNLS.2019.2929575.
  6. ↑ M. E. Hossain, A. Islam and M. S. Islam, "A Proficient Model to Classify Bangladeshi Bank Notes for Automatic Vending Machine Using a Tıny Dataset with One-Shot Learning & Siamese Networks," 2020 11th International Conference on Computing, Communication and Networking Technologies (ICCCNT), Kharagpur, India, 2020, pp. 1-4, doi: 10.1109/ICCCNT49239.2020.9225405.
  7. ↑ S. Bhati, L. M. Velazquez, J. Villalba and N. Dehak, "LSTM Siamese Network for Parkinson’s Disease Detection from Speech," 2019 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Ottawa, ON, Canada, 2019, pp. 1-5, doi: 10.1109/GlobalSIP45357.2019.8969430.
  8. ↑ I. O. de Oliveira, K. V. O. Fonseca and R. Minetto, "A Two-Stream Siamese Neural Network for Vehicle Re-Identification by Using Non-Overlapping Cameras," 2019 IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 2019, pp. 669-673, doi: 10.1109/ICIP.2019.8803810.
  9. ↑ M. Turk and A. Pentland, “Eigenfaces for recognition,” Journal of cognitive neuroscience, vol. 3, no. 1, pp. 71–86, 1991.

Источники информации

  • Lev V. Utkin, Maxim S. Kovalev, Ernest M. Kasimov, "An explanation method for Siamese neural networks", 2019. [2]
  • A. Nandy, S. Haldar, S. Banerjee and S. Mitra, "A Survey on Applications of Siamese Neural Networks in Computer Vision," 2020 International Conference for Emerging Technology (INCET), Belgaum, India, 2020, pp. 1-5, doi: 10.1109/INCET49848.2020.9153977.
  • H. Wu, Z. Xu, J. Zhang, W. Yan and X. Ma, "Face recognition based on convolution siamese networks," 2017 10th International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI), Shanghai, 2017, pp. 1-5, doi: 10.1109/CISP-BMEI.2017.8302003.
Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Сиамская_нейронная_сеть&oldid=75675»