Коды Прюфера

НЕТ ВОЙНЕ

24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян. Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием. Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей. Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить. Антивоенный комитет России

Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению.

meduza.io, Популярная политика, Новая газета, zona.media, Майкл Наки.

Алгоритм построения кодов Прюфера

Кодирование Прюфера переводит помеченные деревья порядка $n$ в последовательность чисел от $1$ до $n$ по алгоритму:
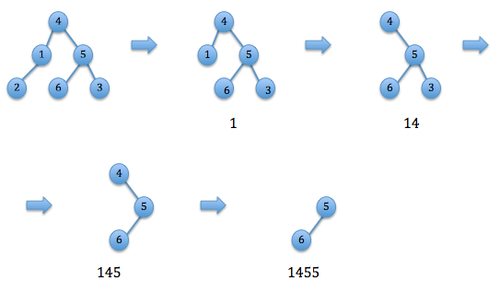
Пока количество вершин больше двух:

1. Выбирается лист $v$ с минимальным номером.
2. В код Прюфера добавляется номер вершины, смежной с $v$.
3. Вершина $v$ и инцидентное ей ребро удаляются из дерева.

Полученная последовательность называется кодом Прюфера (англ. Prüfer code) для заданного дерева.

Лемма:

Номер вершины $v$ встречается в коде Прюфера тогда и только тогда, когда $v$ не является листом, причём встречается этот номер к коде дерева в точности $\deg v - 1$ раз.

Доказательство:

$\triangleright$

Вершина с номером $n$ не может быть удалена, следовательно на последнем шаге у неё была смежная вершина, и число $n$ встретилось в коде. Если вершина не является листом, то у неё на некотором шаге была смежная вершина $-$ лист, следовательно номер этой вершины встречается в коде. Если вершина является листом с номером меньше $n$, то она была удалена до того, как был удален её сосед, следовательно её номер не встречается в коде. Таким образом, номера всех вершин, не являющихся листьями или имеющих номер $n$, встречаются в коде Прюфера, а остальные $-$ нет.

$\triangleleft$

Лемма:

По любой последовательности длины $n - 2$ из чисел от $1$ до $n$ можно построить помеченное дерево, для которого эта последовательность является кодом Прюфера.

Доказательство:

$\triangleright$

Доказательство проведем по индукции по числу $n$ База индукции: $n = 1$ $-$ верно. Индукционный переход: Пусть для числа $n$ верно, построим доказательство для $n+1$: Пусть у нас есть последовательность: $A = [a_1, a_2, ..., a_{n - 2}].$ Выберем минимальное число $v$ не лежащее в $A$. По предыдущей лемме $v$ $-$ вершина, которую мы удалили первой. Соединим $v$ и $a_1$ ребром. Выкинем из последовательности $A$ число $a_1$. Перенумеруем вершины, для всех $a_i \gt v$ заменим $a_i$ на $a_i - 1$. А теперь мы можем применить предположение индукции.

$\triangleleft$

Теорема:

Кодирование Прюфера задаёт биекцию между множествами помеченных деревьев порядка $n$ и последовательностями длиной $n - 2$ из чисел от $1$ до $n$

Доказательство:

$\triangleright$

Каждому помеченному дереву приведенный алгоритм сопоставляет последовательность. Каждой последовательности, как следует из предыдущей леммы, соотвествует помеченное дерево.

$\triangleleft$

Следствием из этой теоремы является формула Кэли.

Пример построения кода Прюфера

Алгоритм декодирования кодa Прюфера

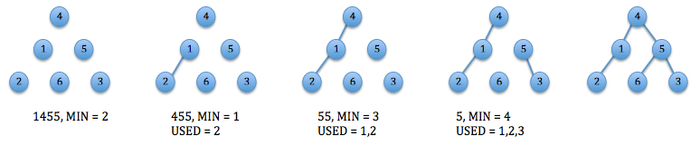
В массиве вершин исходного дерева $V$ найдём вершину $v_{min}$ с минимальным номером, не содержащуюся в массиве с кодом Прюфера $P$, т.е. такую, что она является листом или концом уже добавленного в граф ребра, т.е. она стала листом в процессе построения кода Прюфера (по первому пункту построения). Вершина $p_1$ была добавлена в код Прюфера как инцидентная листу с минимальным номером (по второму пункту построения), поэтому в исходном дереве существует ребро {$p_1$, $v_{min}$}, добавим его в список ребер. Удалим первый элемент из массива $Р$, а вершину $v_{min}$ - из массива $V$ т.к. она больше не может являться листом (по третьему пункту построения). Будем выполнять вышеуказанные действия, пока массив $P$ не станет пустым. В конце работы алгоритма в массиве $V$ останутся две вершины, составляющие последнее ребро дерева (это следует из построения).

Реализация

# P - код Прюфера
# V - вершины
function buildTree(P, V):
   while not P.empty():
      u = P[0]
      v = min(x $\in$ V: P.count(x) == 0)
      G.push({u, v})
      P.erase(0)
      V.erase(indexOf(v))
   G.push({v[0], v[1]})
   return G

Пример декодирования кода Прюфера

См. также

• Связь матрицы Кирхгофа и матрицы инцидентности
• Матрица Кирхгофа
• Количество помеченных деревьев
• Подсчет числа остовных деревьев с помощью матрицы Кирхгофа

Источники информации

• Университет INTUIT | Представление с помощью списка ребер и кода Прюфера