Изменения

{{Теорема|about=Теорема Менгера для вершинной представляет собой группу теорем, связывающих такие понятия на графах как ''<tex>k</tex> связности|statement=Наименьшее число -связность'' и ''количество непересекающихся путей'' относительно двух выделенных вершин. Возникают различные варианты очень похожих друг на друга по формулировке теорем в зависимости от того, рассматриваем ли мы ситуацию в ''ориентированном'' или ''неориентированном'' графе, разделяющих две несмежные вершины и подразумеваем ли ''реберную <tex>sk</tex> -связность'' и ''реберно непересекающиеся пути'' или же ''вершинную <tex>tk</tex>, равно наибольшему числу непересекающихся простых <tex>(s-t)</tex> цепей|proof=связность'' и ''вершинно непересекающиеся пути''.

Очевидно, что если <tex>k</tex> вершин разделяют <tex>s</tex> и <tex>t</tex>==Подготовка к доказательству==Для доказательства мы будем пользоваться развитой раннее [[Определение сети, то сущесвует не более <tex>k</tex> непересекающихся простых <tex>(s-t)</tex> цепейпотока|теорией потоков]].Теперь покажемКроме базовых определений нам потребуется понятие [[Дополняющая сеть, что если <tex>k</tex> вершин графа разделяют <tex>s</tex> и <tex>t</tex>, то существует <tex>k</tex> непересекающихся простых <tex>дополняющий путь| остаточной сети]] (sиначе {{-t)</tex> цепей. Для <tex>k=1</tex> это очевидно. Пусть, для некоторого <tex>k>1</tex> это неверно. Возьмем <tex>h</tex> - наименьшее такое <tex>k</tex> и <tex>F</tex> - граф с наименьшим числом вершин, для которого при выбранном <tex>h</tex> теорема не верна. Будем удалять из <tex>F</tex> ребра, пока не получим <tex>G</tex> такой, что в <tex>G</tex> <tex>s</tex> и <tex>t</tex> разделяют <tex>h</tex> вершин}} дополнительной сети), а в <tex>Gтакже [[Теорема_Форда-x</tex> <tex>h-1</tex> вершина, где <tex>x</tex> Фалкерсона|теорема Форда- произвольное ребро графа <tex>G</tex>Фалкерсона]].

Из определения <tex>G</tex> следует:# В начале берем какой-нибудь поток за начальный (например, что для всякого его ребра <tex>x</tex> существует множество <tex>S(xнулевой)</tex> из <tex>h-1</tex> вершин, которое в <tex>G-x</tex> разделяет <tex>s</tex> и <tex>t</tex>. Далее, граф <tex>G:# В остаточной сети этого потока находим какой-S(x)</tex> содержит по крайней мере одну <tex>(s-t)</tex> цепь, так как граф <tex>G</tex> имеет <tex>h</tex> вершин, разделяющих <tex>s</tex> нибудь путь из источника к стоку и <tex>t</tex> в <tex>G</tex>увеличиваем поток на пропускную способность этого пути. Каждая такая :# Повторяем пункт <tex>(s-t)</tex> цепь должна содержать ребро <tex>x=uv2</tex>до тех пор, поскольку она не является цепью в <tex>Gпока находится хоть какой-x</tex>. Поэтому <tex>u,v \notin S(x)</tex>, и если <tex>u \neq s,t </tex> то <tex>S(x) \cup {u}</tex> разделяет <tex>s</tex> и <tex>t</tex> путь в <tex>G</tex>остаточной сети.

{{Лемма|about=I|statement=В графе <tex>G</tex> нет вершин:То, смежных одновременно с <tex>s</tex> и <tex>t</tex>|proof=Если что получится в <tex>G</tex> есть вершина <tex>w</tex>конце, смежная как с <tex>s</tex>будет максимальным потоком. В случае целочисленной сети достаточно в качестве начального приближения взять нулевой поток, так и с <tex>t</tex>не трудно видеть, то что на каждой итерации (в графе <tex>G-w</tex> для разделения <tex>s</tex> том числе и <tex>t</tex> требуется <tex>h - 1</tex> непересекающихся <tex>(s-t)</tex> цепей. Добавляя <tex>w</tex>, получаем в графе <tex>G</tex> <tex>h</tex> непересекающихся <tex>(s-tпоследней)</tex> цепейэтот поток будет оставаться целочисленным, что противоречит предположению о графе <tex>F</tex>и докажет требуемое.

И, наконец, сделаем немного более осознанным в общем-то и так интуитивно понятное утверждение:{{Лемма|about=IIУтверждение|statement=Любой набор Если в сети, где все пропускные способности ребер равны <tex>W1</tex>, содержащий <tex>h</tex> вершин и разделяющий существует целочисленный поток величиной <tex>sL</tex> то существует и <tex>t</tex> является смежным с <tex>s</tex> или <tex>tL</tex> реберно непересекающихся путей.

Пусть : Считаем, что <tex>Wu</tex> {{- произвольный набор --}} источник, <tex>hv</tex> вершин{{---}} сток.: В начале поймем, что если поток не нулевой, разделяющих то существует маршрут из <tex>su</tex> и в <tex>tv</tex> в лежащий только на ребрах с потоком равным <tex>G1</tex>. ЦепьВ самом деле, соединяющую s с некоторой вершиной <tex>w_i \in W</tex> и если бы такого маршрута не содержащую других существовало, то можно было бы выделить множество вершин до которых такие маршруты из W будем называть вершины <tex>(s-W)u</tex> цепью. Аналогично назовем существуют, не включающее <tex>(W-t)v</tex> цепь, и по нему построить разрез. Обозначим наборы всех <tex>Поток через такой разрез, очевидно равен нулю, видим противоречие (s-W)</tex> и <tex>(W-t)</tex> цепей <tex>P_s</tex> и <tex>P_t</tex> соответственнот.к.Тогда каждая <tex>f(s-tU,V)=|f|</tex> цепь начинается с элемента из <tex>P_s</tex> и заканчивается элементом из <tex>P_t</tex>, поскольку любая цепь содержит вершину из <tex>W</tex>смотри [[Разрез, лемма о потоке через разрез|первую лемму]]). Общие вершины цепей из <tex>P_s</tex> и <tex>P_t</tex> принадлежат набору <tex>W</tex> :Итак, так как по крайней мере одна цепь найдем какой-нибудь маршрут из каждого набора <tex>P_su</tex> и в <tex>P_tv</tex> содержит (любую) вершину лежащий только на ребрах где поток равен <tex>w_i1</tex>, и если бы существовала некоторая вершина, не принадлежащая набору <tex>W</tex>, но содержащаяся сразу и . Удалив все ребра находящиеся в <tex>(s-W)</tex> этом маршруте и в <tex>(W-t)</tex> цепиоставив все остальное неизменным, то нашлась бы придем к целочисленному потоку величиной <tex>(sL-t)</tex> цепь, не имеющая вершин из <tex>W1</tex>. НаконецЯсно, выполняется либо равенство что можно повторить тоже самое еще <tex>P_sL-W={s}1</tex>раз, либо равенство <tex>P_t - W={t}</tex>и, поскольку в противном случае либо таким образом мы выделим <tex>P_sL</tex> вместе с ребрами <math>\{w_1t,w_2t...\}</math>, либо <math>P_t</math> вместе с ребрами <math>\{sw_1,sw_2...\}</math> образуют связные графы с меньшим числом вершин, чем у G, в которых s и t не смежны, и, следовательно, в каждом из них имеется h реберно непересекающихся (s-t) цепей. Объединяя (s-W) и (W-t) части этих цепей, образуем в графе G h непересекающихся (s-t) цепей. Мы пришли к противоречию. Утверждение доказаномаршрутов.

{{Теорема|about=Менгера о реберной двойственности в ориентированном графе|statement=Между вершинами <tex>u</tex> и <tex>v</tex> существует <tex>L</tex> реберно непересекающихся путей тогда и только тогда, когда после удаления любых <tex>(L-1)</tex> ребер существует путь из <tex>u</tex> в <tex>v</tex>.|proof=<tex>\Leftarrow</tex> :Как и прежде, пусть <tex>u</tex> {{---}}источник, а <tex>v</tex> {{---}} сток. :Назначим каждому ребру пропускную способность <tex>1</tex>. Тогда существует максимальный поток, целочисленный на каждом ребре (по лемме). :По теореме Форда-Фалкерсона для такого потока существует разрез с пропускной способностью равной потоку. Удалим в этом разрезе <tex>L-1</tex> ребер, и тогда, раз <tex>u</tex> и <tex>v</tex> находятся в разных частях разреза и, существует путь из <tex>u</tex> в <tex>v</tex>, то в разрезе останется хотя бы еще одно ребро. Это значит, что пропускная способность разреза и вместе с ним величина потока не меньше <tex>L</tex>. А так как поток целочисленный, то это и означает, что найдется <tex> L</tex> реберно непересекающихся путей.

{{Теорема<tex>\Rightarrow</tex> |about=Теорема Менгера для k связности :Существует <tex> L</tex> реберно непересекающихся путей, а значит, удалив любые <tex>L-1</tex> ребер хотя бы один путь останется не тронутым (альтернативная формулировкапринцип Дирихле)|statement=Две несмежные вершины k-отделимы тогда . Это и только тогдаозначает, когда они k-соединимычто существует путь из <tex>u</tex> в <tex>v</tex>.

|about=Теорема Менгера для k-реберной связностио вершинной двойственности в ориентированном графе|statement=Пусть G - конечный, неориентированный граф, Между вершинами <mathtex>\lambda(G) = ku</mathtex> и <mathtex>\Leftrightarrowv</mathtex> для всех пар вершин существует <mathtex>xL</tex> вершинно непересекающихся путей тогда и только тогда, y \in Gкогда после удаления любых <tex>(L-1)</mathtex> вершин существует k реберно непересекающихся путей путь из x <tex>u</tex> в y<tex>v</tex>.

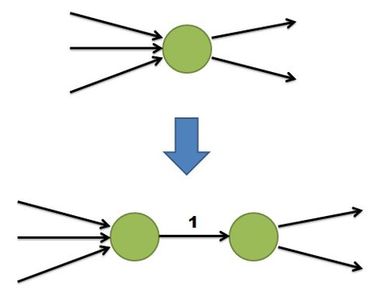
Аналогично :Разобьем каждую вершину на две таким образом: :[[Файл:Menger-vertex.JPG]] :''(все входящие ребра заходят в левую вершину, исходящие выходят из правой. между двумя новыми вершинами добавляем ребро)'' :Теперь задача практически сведена к первой теореме для вершинной связности.:Необходимо лишь отметить, что если в старом графе пути вершинно пересекаются, то в новом графе пути необходимо реберно пересекаются и наоборот.:Кроме того, предложение "удалить в исходном графе любые <tex>L</tex> вершин" можно заменять на "в новом графе можно удалить любые <tex>L</tex> ребер" (достаточно выбирать вершины на концах этих ребер). Можно заменять и обратно, если учесть, что можно удалять ребра между парой вершин, которые раньше были одним целым.