|
|
| Строка 1: |
Строка 1: |
| − | {| class="wikitable" align="center" style="color: red; background-color: black; font-size: 56px; width: 800px;"
| |
| − | |+
| |
| − | |-align="center"
| |
| − | |'''НЕТ ВОЙНЕ'''
| |
| − | |-style="font-size: 16px;"
| |
| − | |
| |
| − | 24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян.
| |
| − |
| |
| − | Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием.
| |
| − |
| |
| − | Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей.
| |
| − |
| |
| − | Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить.
| |
| − |
| |
| − | ''Антивоенный комитет России''
| |
| − | |-style="font-size: 16px;"
| |
| − | |Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению.
| |
| − | |-style="font-size: 16px;"
| |
| − | |[https://meduza.io/ meduza.io], [https://www.youtube.com/c/popularpolitics/videos Популярная политика], [https://novayagazeta.ru/ Новая газета], [https://zona.media/ zona.media], [https://www.youtube.com/c/MackNack/videos Майкл Наки].
| |
| − | |}
| |
| − |
| |
| | {{Определение | | {{Определение |
| | |definition = | | |definition = |
Текущая версия на 19:12, 4 сентября 2022
| Определение: |
| Определим детерминированный автомат с магазинной памятью, допускающий по пустому стеку (англ. PDA accepting by empty stack), как детерминированный автомат с магазинной памятью, у которого нет множества [math]T[/math] допускающих состояний. Автомат заканчивает свою работу как только стек становится пустым. |
Определим для него множество допускающих слов [math]N = \{\omega \mid (q_0,a_0,Z_0)\vdash^* (p,\epsilon,\epsilon)\}[/math], где [math]p[/math] — произвольное состояние.
| Определение: |
| Язык называется беспрефиксным (англ. prefix-free), если для любой пары слов из этого языка ни одно из этих слов не является префиксом другого. |
| Теорема: |
Язык [math]L[/math] допускается ДМП-автоматом, допускающему по пустому стеку тогда и только тогда, когда язык [math]L[/math] допускается ДМП-автоматом, допускающему по допускающему состоянию и [math]L[/math] — беспрефиксный. |
| Доказательство: |
| [math]\triangleright[/math] |
|
[math]\Rightarrow[/math]
- Допустим, что [math]L[/math] не беспрефиксный. Тогда [math]\exists \omega_1, \omega_2 \in L : \omega_2 = \omega_1 \alpha[/math]. Попробуем допустить слово [math]\omega_2[/math]. Тогда автомат остановится сразу после префикса [math]\omega_1[/math], т.к. [math]\omega_1 \in L[/math]. Стек будет пустой, однако до конца слова [math]\omega_2[/math] мы не дойдем, поэтому оно не допустится, хотя содержится в [math]L[/math]. Получили противоречие, значит [math]L[/math] — беспрефиксный.
Построим по заданному ДМП-автомату с допуском по пустому стеку ДМП с допуском по допускающему состоянию.
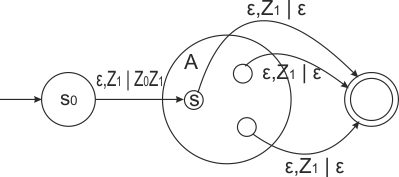
[math]\Leftarrow[/math]
- Пусть задан ДМП-автомат с допуском по допускающему состоянию, язык [math]L[/math] — беспрефиксный. Если автомат в какой-то момент пришел в допускающее состояние, то дальше идти смысла нет, т.к. тогда бы слово, допускаемое этим состоянием было бы префиксом некоторого другого слова. Значит можем удалить все переходы из допускающих состояний и добавить переходы в очистку стека.
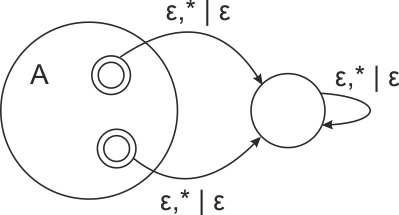 |
| [math]\triangleleft[/math] |
См. также
Источники информации
- Хопкрофт Д., Мотвани Р., Ульман Д. — Введение в теорию автоматов, языков и вычислений, 2-е изд. : Пер. с англ. — Москва, Издательский дом «Вильямс», 2008. : ISBN 978-5-8459-1347-0 (рус.)

