Обучение с частичным привлечением учителя — различия между версиями
Romanosov (обсуждение | вклад) (→Совместное обучение (Co-training)) |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 22 промежуточные версии 2 участников) | |||
| Строка 3: | Строка 3: | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | '''Обучение с частичным привлечением учителя''' (англ. semi-supervised learning, SSL) {{---}} разновидность [[Общие понятия#Классификация задач машинного обучения|обучения с учителем]], которое помимо размеченных данных для обучения также использует неразмеченные данные {{---}} обычно в сравнительно большем количестве. | + | '''Обучение с частичным привлечением учителя''' (англ. semi-supervised learning, SSL) {{---}} разновидность [[Общие понятия#Классификация задач машинного обучения|обучения с учителем]], которое помимо размеченных данных для обучения также использует неразмеченные данные {{---}} обычно в сравнительно большем количестве, чем размеченные. |
}} | }} | ||
| − | |||
== Основная идея == | == Основная идея == | ||
| Строка 13: | Строка 12: | ||
'''Дано''' <br /> | '''Дано''' <br /> | ||
| − | * Множество данных $X = \{x_1, x_2, ... , x_m\}$ и множество меток $Y = \{y_1, y_2, ... , | + | * Множество данных $X = \{x_1, x_2, ... , x_m\}$ и множество меток $Y = \{y_1, y_2, ... , y_l\}$ |
* Размеченные данные вида $(X_l, Y_l) = \{(x_{1:l}, y_{1:l})\}$ | * Размеченные данные вида $(X_l, Y_l) = \{(x_{1:l}, y_{1:l})\}$ | ||
* Множество неразмеченных данных $X_u = \{x_{l+1:n}\}$, используемых в обучении | * Множество неразмеченных данных $X_u = \{x_{l+1:n}\}$, используемых в обучении | ||
| Строка 34: | Строка 33: | ||
=== Предположение кластеризованности (Cluster Assumption) === | === Предположение кластеризованности (Cluster Assumption) === | ||
| − | Допустим, что данные каждого из класса образуют [[Кластеризация|кластеры]]. | + | Допустим, что данные каждого из класса образуют [[Кластеризация|кластеры]]. Если использовать алгоритм кластеризации, используя размеченные данные для присвоения меток кластерам, тогда неразмеченные данные могут быть полезны в более точном нахождении границ этих кластеров. |
'''Cluster Assumption''' {{---}} ''две точки $x_1$, $x_2$ из одного кластера с большей вероятностью имеют одинаковые метки $y_1$, $y_2$.'' | '''Cluster Assumption''' {{---}} ''две точки $x_1$, $x_2$ из одного кластера с большей вероятностью имеют одинаковые метки $y_1$, $y_2$.'' | ||
| Строка 41: | Строка 40: | ||
=== Предположение избыточности (Manifold Assumption) === | === Предположение избыточности (Manifold Assumption) === | ||
| + | |||
| + | [[File:Manifold example.png|thumb|400px|Нелинейное снижение размерности (isomap) формирует томографическое предствление вариантов изображений трёхмерного объекта, используя два угловых параметра: азимут и высоту. Интерполяция изображений (A), экстраполяция (B) и аналогия (C) могут быть вычислены при помощи линейных операций в пространстве признаков.]] | ||
'''Manifold Assumption''' {{---}} ''избыточность данных высокой размерности способствует [[Уменьшение размерности|понижению размерности]].'' | '''Manifold Assumption''' {{---}} ''избыточность данных высокой размерности способствует [[Уменьшение размерности|понижению размерности]].'' | ||
| − | Это предположение применимо, когда измерения данных избыточны, то есть генерируются определенным процессом, имеющим только несколько степеней свободы. В этом случае неразмеченные данные позволяют изучить генерирующий процесс и за счёт этого снизить размерность, что упрощает, например, привязку предположения плавности. | + | Это предположение применимо, когда измерения данных избыточны, то есть генерируются определенным процессом, имеющим только несколько степеней свободы. |
| + | Иначе говоря, вместо использования предположения, что данные могут представлять из себя любые объекты из многомерного пространства (например, множество из всех возможных изображений размером 1 мегапиксель, включая белый шум), легче представить эти данные в пространстве более низкой размерности, исключая разными способами конфигурации пикселей, которые не характерны для конкретных данных. В этом случае неразмеченные данные позволяют изучить генерирующий процесс и за счёт этого снизить размерность, что упрощает, например, привязку предположения плавности. | ||
| + | |||
| + | '''Пример''' | ||
| + | |||
| + | Рассмотрим задачу обнаружения признаков на примере перцепции. Множество двухмерных отображений трёхмерного объекта со всех возможных углов обзора имеет весьма высокую размерность, будучи представленным в виде массивов изображений в памяти вычислительной машины; чёрно-белые картинки размером 32x32 пикселя можно понимать как точки 1024-мерного пространства углов обзора (пространство входных данных). Более значимая для перцепции структура (пространство признаков), однако, может гораздо более низкую размерность: эти же изображения могут лежать в 2-мерном многообразии, параметризованном с помощью углов обзора (см. иллюстрацию). | ||
| + | |||
| + | Другим примером задач, когда естественные данные являются избыточными, является [[Векторное представление слов|векторное представление слов]] и [[Обработка естественного языка|обработка естественного языка]]. | ||
== Подходы к решению задачи == | == Подходы к решению задачи == | ||
| Строка 74: | Строка 82: | ||
* Негативное влияние ошибочных прогнозов усиливается с обучением. В таком случае существуют эвристические решения, например "удаление" метки с объекта, достоверность прогноза которого оказалась ниже определённого порога | * Негативное влияние ошибочных прогнозов усиливается с обучением. В таком случае существуют эвристические решения, например "удаление" метки с объекта, достоверность прогноза которого оказалась ниже определённого порога | ||
| − | * Трудно достичь сходимости алгоритма. Однако, существуют частные случаи, когда самообучение эквивалентно работе [[EM-алгоритм|EM-алгоритма]], | + | * Трудно достичь сходимости алгоритма. |
| + | |||
| + | Однако, существуют частные случаи, когда самообучение эквивалентно работе [[EM-алгоритм|EM-алгоритма]], например его модификация под байесовский классификатор, использующий неразмеченные данные. Также у задач, использующих некоторые классы функций (например, линейные), существуют решения в виде сходящегося алгоритма. | ||
=== Совместное обучение (Co-training) === | === Совместное обучение (Co-training) === | ||
| Строка 82: | Строка 92: | ||
'''Разделение признаков (feature split)''' <br> | '''Разделение признаков (feature split)''' <br> | ||
| − | Метод совместного | + | Метод совместного обучения предполагает, что каждый объект имеет два множества признаков $x = [x^{(1)}; x^{(2)}]$, разделение между которыми может быть как естественным, так и искусственным. Примером объекта с естественным разделением признаков может послужить веб-страница, содержащая текст и изображения. Два независимых классификатора обучаются по двум множествам признаков: первый анализирует текст, второй {{---}} изображения. |
'''Предположения, используемые в совместном обучении''' | '''Предположения, используемые в совместном обучении''' | ||
| Строка 101: | Строка 111: | ||
* Подходит почти ко всем известным классификаторам в качестве обёртки | * Подходит почти ко всем известным классификаторам в качестве обёртки | ||
| − | * Не так сильна чувствительность к ошибочным прогнозам, по | + | * Не так сильна чувствительность к ошибочным прогнозам, по сравнению с self-training |
'''Недостатки''' | '''Недостатки''' | ||
| Строка 119: | Строка 129: | ||
'''Пример генеративной модели''' | '''Пример генеративной модели''' | ||
| − | Параметры модели: $\theta = \{w_1, w_2, \mu_1, \mu_2, \sum_1, \sum_2\}$ | + | Параметры модели: $\theta = \big{\{}w_1, w_2, \mu_1, \mu_2, \sum_1, \sum_2\big{\}}$ |
Модель: | Модель: | ||
| − | $p(x, y|\theta) = p(y|\theta)p(x|y,\theta) = w_yN(x;\mu_y,\sum_y)$ | + | $p(x, y|\theta) = p(y|\theta)p(x|y,\theta) = w_yN\big(x;\mu_y,\sum_y\big)$ |
Классификация: | Классификация: | ||
| − | $p(y|x,\theta) = \frac{p(x,y|\theta)}{\sum_{y'}p(x,y'|\theta)}$ | + | $p(y|x,\theta) = \large{\frac{p(x,y|\theta)}{\sum_{y'}p(x,y'|\theta)}}$ |
| − | '''Достоинства''' | + | Разберём пример двоичной классификации с использованием принципа максимального правдоподобия (''MLE''). |
| + | |||
| + | Размеченные данные имеют вид <br> | ||
| + | $\log p(X_l, Y_l|\theta) = \sum\limits_{i = 1}^l \log p(y_i|\theta)p(x_i|y_i, \theta)$ <br> | ||
| + | Здесь в качестве оценки MLE для $\theta$ возьмём тривиальные величины: частота, выборочное среднее, выборочная ковариация. | ||
| + | |||
| + | Размеченные и неразмеченные данные: <br> | ||
| + | $\log p(X_l, Y_l, X_u|\theta) = \sum\limits_{i = 1}^l \log p(y_i|\theta)p(x_i|y_i, \theta) + \sum\limits_{i = l+1}^{l+u} \log \big(\sum\limits_{y=1}^2 p(y|\theta)p(x_i|y, \theta)\big)$ <br> | ||
| + | Теперь, с появлением скрытых переменных, оценка MLE теряет тривиальность, однако для поиска локального оптимума можно использовать [[EM-алгоритм|EM-алгоритм]]. | ||
| + | |||
| + | '''Достоинства генеративных моделей''' | ||
* Гереативные модели очень эффективны, если составленная модель близка к правильной | * Гереативные модели очень эффективны, если составленная модель близка к правильной | ||
| Строка 140: | Строка 160: | ||
=== Полуавтоматические [[Метод опорных векторов (SVM)|опорные вектора]] (S3VM) === | === Полуавтоматические [[Метод опорных векторов (SVM)|опорные вектора]] (S3VM) === | ||
| − | [[File:S3VM-margin.png|thumb| | + | [[File:S3VM-margin.png|thumb|400px|Зазор, разделяющий неразмеченные данные]] |
Полуавтоматические SVM (англ. ''Semi-supervised SVMs'', ''S3VMs''), они же ''трансдуктивные SVM'' (TSVMs) решают задачу максимизации зазора (''margin'') между неразмеченными данными. | Полуавтоматические SVM (англ. ''Semi-supervised SVMs'', ''S3VMs''), они же ''трансдуктивные SVM'' (TSVMs) решают задачу максимизации зазора (''margin'') между неразмеченными данными. | ||
| Строка 175: | Строка 195: | ||
* Трудности в оптимизации | * Трудности в оптимизации | ||
* Алгоритм может сходиться к неправильной (''плохой'') целевой функции | * Алгоритм может сходиться к неправильной (''плохой'') целевой функции | ||
| − | * Менее мощный подход, по | + | * Менее мощный подход, по сравнению с алгоритмами на графах и генеративными моделями, т. е. потенциально менее эффективное обучение |
=== Алгоритмы на основе [[Теория графов|графов]] === | === Алгоритмы на основе [[Теория графов|графов]] === | ||
| + | |||
| + | [[File:digits Euclidean.png|thumb|400px|Изображения рукописных цифр. <br>Слева {{---}} две цифры с большим евклидовым расстоянием, но одинаковой меткой класса. <br>Справа {{---}} те же цифры, "соединённые" неразмеченной последовательностью (путь в графе), где каждые две соседние цифры имеют малое евклидово расстояние.]] | ||
| + | |||
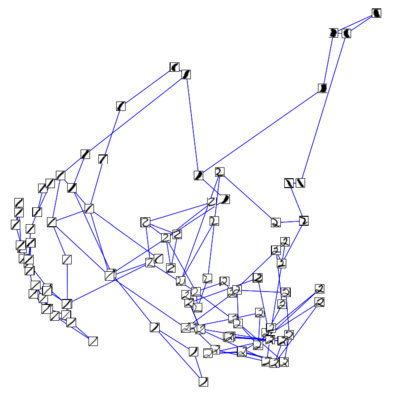
| + | [[File:digits Euclidean graph.png|thumb|400px|Граф, построенный на множестве рукописных цифр "1" и "2".]] | ||
Данные можно представить в виде графа, построенного с использованием знаний в предметной области или на основе сходства объектов. | Данные можно представить в виде графа, построенного с использованием знаний в предметной области или на основе сходства объектов. | ||
| Строка 198: | Строка 222: | ||
4. Классифицируем новый объект $x$ из тестового множества, используя $sign(f(x))$ | 4. Классифицируем новый объект $x$ из тестового множества, используя $sign(f(x))$ | ||
| + | |||
| + | '''Пример''' | ||
| + | |||
| + | Графы, формирующиеся в процессе обучения, как правило, достаточно объёмны для графического отображения и человеческого восприятия. Для большей ясности рассмотрим множество данных, состоящее только из рукописных цифр "1" и "2". Критерием сходства объектов послужит евклидово расстояние, которое бывает особенно полезно при поиске локального сходства. Если такое расстояние между объектами достаточно мало, мы можем предположить, что объекты принадлежат одному классу. На основе расстояния можно построить [[Метрический классификатор и метод ближайших соседей|KNN]]-граф (см. иллюстрацию), где объекты с малым евклидовым расстоянием будут соединены рёбрами. Чем больше имеется неразмеченных данных, схожих с размеченными (см. пример с цифрой "2"), тем больше соотвествующих рёбер, и, следовательно, более высокая точность классификации. | ||
'''Достоинства алгоритмов на графах''' | '''Достоинства алгоритмов на графах''' | ||
| Строка 206: | Строка 234: | ||
'''Недостатки''' | '''Недостатки''' | ||
| − | * Низкая эффективность при плохом | + | * Низкая эффективность при плохом построении графа |
* Зависимость от структуры графа и весов рёбер | * Зависимость от структуры графа и весов рёбер | ||
| Строка 219: | Строка 247: | ||
# [http://pages.cs.wisc.edu/~jerryzhu/pub/sslicml07.pdf Semi-SuperVised Learning Tutorial] | # [http://pages.cs.wisc.edu/~jerryzhu/pub/sslicml07.pdf Semi-SuperVised Learning Tutorial] | ||
# [https://www.molgen.mpg.de/3659531/MITPress--SemiSupervised-Learning.pdf MIT Press {{---}} Semi-Supervised Learning] | # [https://www.molgen.mpg.de/3659531/MITPress--SemiSupervised-Learning.pdf MIT Press {{---}} Semi-Supervised Learning] | ||
| + | # [http://web.mit.edu/cocosci/Papers/man_nips.pdf Mapping a manifold of perceptual observations] | ||
| + | # [http://pages.cs.wisc.edu/~jerryzhu/pub/thesis.pdf Semi-Supervised Learning with Graphs] | ||
[[Категория:Машинное обучение]] | [[Категория:Машинное обучение]] | ||
[[Категория:Обучение с частичным привлечением учителя]] | [[Категория:Обучение с частичным привлечением учителя]] | ||
Текущая версия на 19:19, 4 сентября 2022
Содержание
Определение
| Определение: |
| Обучение с частичным привлечением учителя (англ. semi-supervised learning, SSL) — разновидность обучения с учителем, которое помимо размеченных данных для обучения также использует неразмеченные данные — обычно в сравнительно большем количестве, чем размеченные. |
Основная идея
Обучение с частичным привлечением учителя занимает промежуточное положение между обучением с учителем и без учителя. Когда получение достаточного количества размеченных данных затруднено (например, когда при разметке данных привлекаются дорогостоящие устройства или квалифицированные лица), помимо размеченных данных можно также задействовать и неразмеченные данные для построения более эффективных моделей, по сравнению с моделями, построенными с полным участием учителя или без него вовсе.
Постановка задачи обучения
Дано
- Множество данных $X = \{x_1, x_2, ... , x_m\}$ и множество меток $Y = \{y_1, y_2, ... , y_l\}$
- Размеченные данные вида $(X_l, Y_l) = \{(x_{1:l}, y_{1:l})\}$
- Множество неразмеченных данных $X_u = \{x_{l+1:n}\}$, используемых в обучении
- Как правило, $l \ll n$
- Множество неразмеченных данных $X_{test} = \{x_{n+1:m}\}$, не используемых в обучении (тестовая выборка)
Найти
- Найти решающую функцию $a: X → Y$, где при нахождении функции подразумевается применение как $(X_l, Y_l)$, так и $X_u$.
Основные предположения, используемые SSL
Как и обучение с учителем, SSL также использует некоторые предположения на этапе распределения неразмеченных данных. Без них не представляется возможным обобщение алгоритма, решающего задачу лишь на одном конечном тестовом множестве данных, на потенциально бесконечное множество последующих тестовых наборов данных.
Предположение плавности (Smoothness Assumption)
Smoothness Assumption — две точки $x_1$, $x_2$ в области высокой плотности, лежащие близко друг от друга, с большей вероятностью имеют одинаковые метки $y_1$, $y_2$.
Более того, исходя из транзитивности, если две точки связаны между собой точками из области высокой плотности (например, принадлежат одному кластеру), то они также, вероятно, размечены одинаково. С другой стороны, предположение даёт преимущество для разграничения в регионах с низкой плотностью, там где меньше близко разположенных точек, но больше вероятность принадлежности к разным классам.
Предположение кластеризованности (Cluster Assumption)
Допустим, что данные каждого из класса образуют кластеры. Если использовать алгоритм кластеризации, используя размеченные данные для присвоения меток кластерам, тогда неразмеченные данные могут быть полезны в более точном нахождении границ этих кластеров.
Cluster Assumption — две точки $x_1$, $x_2$ из одного кластера с большей вероятностью имеют одинаковые метки $y_1$, $y_2$.
Предположение обосновывается на явном существовании классов: если существует плотный континуум объектов, маловероятно, что он будет разделён на разные классы. Следует отметить, что предположение не подразумевает формирования одного компактного кластера одним классом, но и не рассматривает два объекта разных классов в одном кластере.
Предположение избыточности (Manifold Assumption)

Manifold Assumption — избыточность данных высокой размерности способствует понижению размерности.
Это предположение применимо, когда измерения данных избыточны, то есть генерируются определенным процессом, имеющим только несколько степеней свободы. Иначе говоря, вместо использования предположения, что данные могут представлять из себя любые объекты из многомерного пространства (например, множество из всех возможных изображений размером 1 мегапиксель, включая белый шум), легче представить эти данные в пространстве более низкой размерности, исключая разными способами конфигурации пикселей, которые не характерны для конкретных данных. В этом случае неразмеченные данные позволяют изучить генерирующий процесс и за счёт этого снизить размерность, что упрощает, например, привязку предположения плавности.
Пример
Рассмотрим задачу обнаружения признаков на примере перцепции. Множество двухмерных отображений трёхмерного объекта со всех возможных углов обзора имеет весьма высокую размерность, будучи представленным в виде массивов изображений в памяти вычислительной машины; чёрно-белые картинки размером 32x32 пикселя можно понимать как точки 1024-мерного пространства углов обзора (пространство входных данных). Более значимая для перцепции структура (пространство признаков), однако, может гораздо более низкую размерность: эти же изображения могут лежать в 2-мерном многообразии, параметризованном с помощью углов обзора (см. иллюстрацию).
Другим примером задач, когда естественные данные являются избыточными, является векторное представление слов и обработка естественного языка.
Подходы к решению задачи
Самообучение (Self Training)
Алгоритм
1. Обучить $f$ с помощью $(X_l, Y_l)$
2. Спрогнозировать $x \in X_u$
3. Добавить $(x, f(x))$ к размеченным данным
4. Повторить
Алгоритм основан на предположении, что достоверные прогнозы, формируемые на шаге 2 — верны.
Вариации самообучения
- Добавление нескольких наиболее достоверных $(x, f(x))$ к размеченным данным
- Добавление всех $(x, f(x))$ к размеченным данным
- Добавление всех $(x, f(x))$ к размеченным данным, взвешивание достоверности каждого $x$
Достоинства метода
- Наиболее простой метод semi-supervised обучения
- Метод может быть обёрткой для более сложных алгоритмов классификации
- Часто используется в прикладных задачах, таких как обработка естественного языка
Недостатки
- Негативное влияние ошибочных прогнозов усиливается с обучением. В таком случае существуют эвристические решения, например "удаление" метки с объекта, достоверность прогноза которого оказалась ниже определённого порога
- Трудно достичь сходимости алгоритма.
Однако, существуют частные случаи, когда самообучение эквивалентно работе EM-алгоритма, например его модификация под байесовский классификатор, использующий неразмеченные данные. Также у задач, использующих некоторые классы функций (например, линейные), существуют решения в виде сходящегося алгоритма.
Совместное обучение (Co-training)
Совместное обучение является расширением самообучения, при котором несколько классификаторов прорабатывают разные (в идеале, непересекающиеся) множества признаков и генерируют размеченные примеры друг для друга.
Разделение признаков (feature split)
Метод совместного обучения предполагает, что каждый объект имеет два множества признаков $x = [x^{(1)}; x^{(2)}]$, разделение между которыми может быть как естественным, так и искусственным. Примером объекта с естественным разделением признаков может послужить веб-страница, содержащая текст и изображения. Два независимых классификатора обучаются по двум множествам признаков: первый анализирует текст, второй — изображения.
Предположения, используемые в совместном обучении
- Естественное разделение признаков $x = [x^{(1)}; x^{(2)}]$ существует
- $x^{(1)}$ и $x^{(2)}$ таковы, что по-отдельности могут обучить хороший классификатор
- множества $x^{(1)}$ и $x^{(2)}$ являются условно независимыми при фиксированном классе
Алгоритм
1. Обучить два классификатора: $f^{(1)}$ с помощью $(X_l^{(1)}, Y_l)$, $f^{(2)}$ с помощью $(X_l^{(2)}, Y_l)$
2. Классифицировать множество $X_u$ с $f^{(1)}$ и $f^{(2)}$ независимо
3. Добавить $k$ наиболее достоверных прогнозов $(x, f^{(1)}(x))$ из $f^{(1)}$ к данным, размеченным с помощью $f^{(2)}$
4. Добавить $k$ наиболее достоверных прогнозов $(x, f^{(2)}(x))$ из $f^{(2)}$ к данным, размеченным с помощью $f^{(1)}$
5. Повторить
Преимущества
- Подходит почти ко всем известным классификаторам в качестве обёртки
- Не так сильна чувствительность к ошибочным прогнозам, по сравнению с self-training
Недостатки
- Естественное разделение признаков не всегда существует. В таком случае можно использовать fake feature split — случайное искуственное разделение
- Необхоимо искать эффективные модели, когда приходится использовать признаки из нескольких множеств
Генеративные модели
Генеративные модели в полуавтоматическом обучении можно рассматривать как расширение обучения с учителем (классификация и информация о $p(x)$, или как расширение обучения без учителя (кластеризация и некоторые метки). Основное предположение генеративных моделей заключается в том, что распределения принимают форму $p(x|y, \theta)$, параметризованную вектором $\theta$.
Идея
- Интересующая величина: $p(X_l, Y_l, X_u|\theta) = \sum_{Y_u}p(X_l, Y_l, X_u, Y_u|\theta)$
- Найти для $\theta$ оценку максимального правдоподобия, оценить апостериорный максимум или использовать теорему Байеса.
Пример генеративной модели
Параметры модели: $\theta = \big{\{}w_1, w_2, \mu_1, \mu_2, \sum_1, \sum_2\big{\}}$
Модель:
$p(x, y|\theta) = p(y|\theta)p(x|y,\theta) = w_yN\big(x;\mu_y,\sum_y\big)$
Классификация:
$p(y|x,\theta) = \large{\frac{p(x,y|\theta)}{\sum_{y'}p(x,y'|\theta)}}$
Разберём пример двоичной классификации с использованием принципа максимального правдоподобия (MLE).
Размеченные данные имеют вид
$\log p(X_l, Y_l|\theta) = \sum\limits_{i = 1}^l \log p(y_i|\theta)p(x_i|y_i, \theta)$
Здесь в качестве оценки MLE для $\theta$ возьмём тривиальные величины: частота, выборочное среднее, выборочная ковариация.
Размеченные и неразмеченные данные:
$\log p(X_l, Y_l, X_u|\theta) = \sum\limits_{i = 1}^l \log p(y_i|\theta)p(x_i|y_i, \theta) + \sum\limits_{i = l+1}^{l+u} \log \big(\sum\limits_{y=1}^2 p(y|\theta)p(x_i|y, \theta)\big)$
Теперь, с появлением скрытых переменных, оценка MLE теряет тривиальность, однако для поиска локального оптимума можно использовать EM-алгоритм.
Достоинства генеративных моделей
- Гереативные модели очень эффективны, если составленная модель близка к правильной
Недостатки
- Трудно определить корректность модели
- Неразмеченные данные могут навредить при использовании неверной генеративной модели
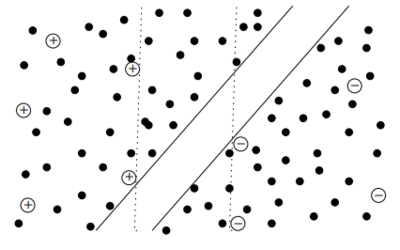
Полуавтоматические опорные вектора (S3VM)
Полуавтоматические SVM (англ. Semi-supervised SVMs, S3VMs), они же трансдуктивные SVM (TSVMs) решают задачу максимизации зазора (margin) между неразмеченными данными.
Идея
- Перечислить все $2^u$ возможные способы разметки множества $X_u$
- Построить стандартную SVM для каждой разметки (и для $X_l$)
- Взять SVM с наибольшим зазором
Постановка задачи
- Два класса $y \in \{+1, -1\}$
- Размеченные данные $(X_l, Y_l)$
- Ядро $K$
- Гильбертово пространство функций $H_K$ (RKHS)
С помощью SVM найти функцию $f(x)=h(x)+b$, где $h \in H_K$ и классифицировать $x$ с помощью $sign(f(x))$
Алгоритм
1. Входные данные: ядро $K$, веса $\lambda_1, \lambda_2, (X_l, Y_l), X_u$
2. Решим задачу оптимизации для $f(x) = h(x) + b, h(x) \in H_K$
${min}_f \sum\limits_{i = 1}^{l} (1 - y_i f(x_i))_+ + \lambda_1\|h\|^2_{H_K} + \lambda_2 \sum\limits_{i = l + 1}^n (1 - |f(x_i)|)_+ $
такую, что $\frac{1}{n-l}\sum\limits_{i=l+1}^n f(x_i) = \frac{1}{l}\sum\limits_{i = 1}^{l}y_i$
4. Классифицируем новый объект $x$ из тестового множества, используя $sign(f(x))$
Достоинства S3VM
- Применимо везде, где применимы классические SVM
Недостатки
- Трудности в оптимизации
- Алгоритм может сходиться к неправильной (плохой) целевой функции
- Менее мощный подход, по сравнению с алгоритмами на графах и генеративными моделями, т. е. потенциально менее эффективное обучение
Алгоритмы на основе графов
Данные можно представить в виде графа, построенного с использованием знаний в предметной области или на основе сходства объектов.
Дано
- Вершины $X_l \cup X_u$
- Рёбра, вычисленные исходя из признаков, например
- $k$ ближайших соседей
- Полный граф, веса рёбер которого убывают с расстоянием, $w = exp(-\|x_i - x_j\|^2/\sigma^2)$
Найти сходство по всем путям.
Регуляризация избыточности
1. Входные данные: ядро $K$, веса $\lambda_1, \lambda_2, (X_l, Y_l), X_u$
2. Построим граф сходств $W$ из вершин $X_l, X_u$, вычислим Лапласиан графа $\Delta$
3. Решим задачу оптимизации для $f(x) = h(x) + b, h(x) \in H_K$
${min}_f \sum\limits_{i = 1}^l (1 - y_i f(x_i))_+ + \lambda_1\|h\|^2_{H_K} + \lambda_2 f_{1:n}^T \Delta f_{1:n} $
4. Классифицируем новый объект $x$ из тестового множества, используя $sign(f(x))$
Пример
Графы, формирующиеся в процессе обучения, как правило, достаточно объёмны для графического отображения и человеческого восприятия. Для большей ясности рассмотрим множество данных, состоящее только из рукописных цифр "1" и "2". Критерием сходства объектов послужит евклидово расстояние, которое бывает особенно полезно при поиске локального сходства. Если такое расстояние между объектами достаточно мало, мы можем предположить, что объекты принадлежат одному классу. На основе расстояния можно построить KNN-граф (см. иллюстрацию), где объекты с малым евклидовым расстоянием будут соединены рёбрами. Чем больше имеется неразмеченных данных, схожих с размеченными (см. пример с цифрой "2"), тем больше соотвествующих рёбер, и, следовательно, более высокая точность классификации.
Достоинства алгоритмов на графах
- Ясный математический аппарат
- Высокая эффективность, когда граф соответствует задаче
- Можно использовать ориентированные графы
Недостатки
- Низкая эффективность при плохом построении графа
- Зависимость от структуры графа и весов рёбер