EM-алгоритм

Определение

Алгоритм EM --- алгоритм поиска максимума правдоподобия параметров для решения задач, где некоторые переменные не являются наблюдаемыми.

Алгоритм ищет параметры модели итеративно, каждая итерация состоит из двух шагов:

E(Expectation) шаг, в котором находится распределение скрытых переменных используя значение наблюдаемых переменных и текущего значения параметров.

M(Maximisation) шаг --- пересчет параметров, находя максимум правдоподобия исходя из распределения скрытых переменных, полученных на E-шаге.

Задача разделения смеси распределений

Общий алгоритм

Необходимо описать плотность распределения функции на X как сумму k функций, которые можно рассматривать как элементы параметрического семейства функций [math] p_j(x) = \phi(x;\theta_j)[/math]. Плотность распределения будет выглядеть как
[math]p(x) = \sum\limits_{i=1}^k \omega_j p_j(x); \sum\limits_{i=1}^k w_j = 1; w_j \gt = 0 [/math]
где [math]\omega_j[/math]- априорная вероятность j компоненты распределения. Задача разделения смеси заключается в том, чтобы, имея выборку [math]X^m[/math] случайных и независимых наблюдений из смеси [math]p(x)[/math], зная число [math]k[/math] и функцию [math]\phi[/math], оценить вектор параметров [math]\theta = (\omega_1,..,\omega_k,\theta_1,..,\theta_k)[/math]

E-шаг:

[math]p(x,\theta_j) = p(x)P(\theta_j | x) = w_jp_j(x)[/math]
Введем обозначение: [math] g_{ij} = P(\theta_j | x_i) [/math] это и будут скрытые параметры данной задачи - апостериорная вероятность того, что обучающий объект [math] x_i [/math] получен из [math]j[/math]-й компоненты

По формуле Байеса справедливо равенство:
[math] g_{ij} = \frac{w_jp_j(x_i)}{\sum\limits_{t=1}^k w_t p_t(x_i)}[/math]
Таким образом при зная значение параметров легко найти скрытые переменные.

Перейдем к M-шагу.

Посчитаем для аддитивности логарифм правдоподобия:
[math] Q(\Theta) = ln \prod\limits_{i=1}^mp(x_i) = \sum\limits_{i=1}^m ln\sum\limits_{j=1}^k w_j p_j(x_i) \longrightarrow max[/math]
при условии [math]\sum\limits_{i=1}^k w_j = 1; w_j \gt = 0[/math] имеет смысл рассматривать лагранжиан задачи:
[math]\frac{\partial L} {\partial w_j} = \sum\limits_{i=1}^m \frac{p_j(x_i)}{\sum\limits_{t=1}^kw_tp_t(x_i)} - \lambda = 0.[/math]

Умножим на [math]\omega_j[/math] и просуммируем уравнения для всех [math]j[/math]

[math]\sum\limits_{j=1}^k \sum\limits_{i=1}^m \frac{w_jp_j(x_i)}{\sum\limits_{t=1}^kw_tp_t(x_i)} = \lambda \sum\limits_{j=1}^kw_j[/math]

Так как можно заменить порядок суммы и [math]\sum\limits_{i=1}^m \frac{w_jp_j(x_i)}{\sum\limits_{t=1}^kw_tp_t(x_i)} = 1[/math] и [math]\sum\limits_{j=1}^kw_j = 1[/math], из чего следует [math]\lambda = m[/math]

[math]\omega_j = \frac{1}{m}\sum\limits_{i=1}^m \frac{w_jp_j(x_i)}{\sum\limits_{t=1}^kw_tp_t(x_i)} = \frac{1}{m}\sum\limits_{i=1}^mg_{ij}[/math]

Приравняв к нулю лагранжиан по [math]\theta_j[/math] схожим способом найдем:

[math] \theta_j = \arg\max\limits{\theta}\sum\limits_{i=1}^mg_{ij}\ln(\phi(x_i;\theta)).[/math]

Таким образом на M-шаге необходимо взять среднее значение [math]g_{ij}[/math] и решить k независимых оптимизационных задач.

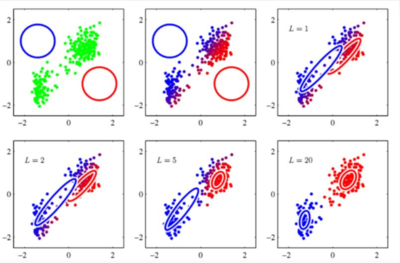
Разделение смеси гауссиан

Важным на практике примером является случай, когда параметрическое семейство - нормальные распределения. Параметрами функций будут являться матожидание и дисперсия.
[math]\theta = (w_1,..,w_k;\;\mu_1,..,\mu_k;\;\sigma_1,..,\sigma_k)[/math] — вектор параметров,
[math]p_j(x) = N(x;\mu_j, \sigma_j) = \frac1{\sqrt{2\pi}\sigma_j} \exp \biggl(-\frac{(x - \mu_j)^2}{2\sigma_j^2}\biggr) [/math]

k-means как EM алгоритм

Скрытыми переменными в данной задаче являются классы, к которым относятся объекты для кластеризации. Сами же параметры это центры масс классов. На шаге E - распределяются все объекты по классам исходя из расстояния от центра, на шаге M находится оптимальное месторасположение центра.

Аналогично рассматривается и алгоритм c-means. Скрытые переменные здесь будут вероятности принадлежности к классам, которые находятся на E-шаге по расстоянию от центра. Центр так же рассчитывается на M-шаге исходя из скрытых переменных.

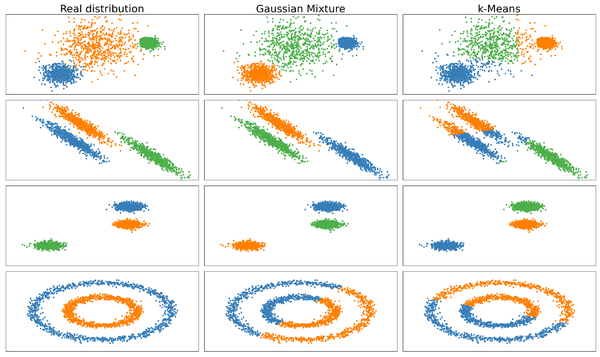
Реализация на python

import numpy as np
import matplotlib.pyplot as plt
from sklearn import cluster, datasets, mixture
from sklearn.preprocessing import StandardScaler
from itertools import cycle, islice
np.random.seed(12)

# Создаем datasets с использованием стандартных sklearn.datasets
n_samples = 2000
random_state = 170
noisy_circles = datasets.make_circles(n_samples=n_samples, factor=.5, noise=.05)
noisy_moons = datasets.make_moons(n_samples=n_samples, noise=.05)
blobs = datasets.make_blobs(n_samples=n_samples, random_state=8)
varied = datasets.make_blobs(n_samples=n_samples, cluster_std=[1.0, 2.5, 0.5], random_state=random_state)

# Создаем анизатропно разделенные данные
X, y = datasets.make_blobs(n_samples=n_samples, random_state=random_state)
transformation = [[0.6, -0.6], [-0.4, 0.8]]
X_aniso = np.dot(X, transformation)
aniso = (X_aniso, y)

# Выставляем параметры для matplotlib.pyplot
plt.figure(figsize=(9 * 2 + 3, 12.5))
plt.subplots_adjust(left=.02, right=.98, bottom=.001, top=.96, wspace=.05, hspace=.01)
plot_num = 1
defaul_n = 3

# Варьируем значение количества классов в зависимости от данных, ведь для нас это гиперпараметр
datasets = [
   (varied, defaul_n),
   (aniso, defaul_n),
   (blobs, defaul_n),
   (noisy_circles, 2)]
for i_dataset, (dataset, n_cluster) in enumerate(datasets):
   X, y = dataset

   # Нормализация данных
   X = StandardScaler().fit_transform(X)

   # Непосредственно наш алгоритм - Gaussian Mixture
   gmm = mixture.GaussianMixture(n_components=n_cluster, covariance_type='full')
   
   # Для сравнения берем алгоритм - K-means
   two_means = cluster.KMeans(n_clusters=n_cluster)
   clustering_algorithms = (
       ('GaussianMixture', gmm),
       ('KMeans', two_means)
   )
   for name, algorithm in clustering_algorithms:

       # Этап обучения
       algorithm.fit(X)
       
       # Применяем алгоритм
       y_pred = algorithm.predict(X)
       
       # Рисуем результаты
       plt.subplot(len(datasets), len(clustering_algorithms), plot_num)
       if i_dataset == 0:
           plt.title(name, size=18)
       colors = np.array(list(islice(cycle(['#377eb8', '#ff7f00', '#4daf4a']), int(max(y_pred) + 1))))
       plt.scatter(X[:, 0], X[:, 1], s=10, color=colors[y_pred])
       plt.xlim(-2.5, 2.5)
       plt.ylim(-2.5, 2.5)
       plt.xticks(())
       plt.yticks(())
       plot_num += 1
plt.show()

Результат программы

Как и следовало ожидать, алгоритм работает на некоторых данных лучше чем k-means, однако есть данные, с которыми он не справляется без дополнительных преобразований.

См. также

• Кластеризация

Источники информации

1. Математические методы обучения по прецедентам К. В. Воронцов
2. k-means