Автоматы с магазинной памятью — различия между версиями
м (rollbackEdits.php mass rollback) |
|||
| (не показано 49 промежуточных версий 12 участников) | |||
| Строка 1: | Строка 1: | ||
| − | |||
==Недетерминированный автомат с магазинной памятью== | ==Недетерминированный автомат с магазинной памятью== | ||
| − | |||
| − | |||
| − | |||
| − | |||
{{Определение | {{Определение | ||
| − | |definition= Автомат с магазинной памятью --- это набор | + | |definition= '''Автомат с магазинной памятью''' (автомат со стеком, англ. ''pushdown automaton'') {{---}} это набор <tex>A=\langle\Sigma,\Gamma,Q,s\in Q, T \subset Q, z_0 \in \Gamma, \delta : Q \times \Sigma \cup \{\varepsilon\} \times \Gamma \rightarrow 2^{Q \times \Gamma^*}\rangle</tex>, где |
| − | *<tex>\Sigma</tex> --- входной алфавит на ленте | + | *<tex>\Sigma</tex> {{---}} входной алфавит на ленте, |
| − | *<tex>\Gamma</tex> --- стековый алфавит | + | *<tex>\Gamma</tex> {{---}} стековый алфавит, |
| − | *<tex>Q</tex> --- множество состояний автомата | + | *<tex>Q</tex> {{---}} множество состояний автомата, |
| − | *<tex>s</tex> --- стартовое состояние автомата | + | *<tex>s</tex> {{---}} стартовое состояние автомата, |
| − | *<tex>T</tex> --- множество допускающих состояний автомата | + | *<tex>T</tex> {{---}} множество допускающих состояний автомата, |
| − | *<tex>z_0</tex> --- маркер дна стека | + | *<tex>z_0</tex> {{---}} маркер дна стека, |
| − | *<tex>\delta</tex> --- функция переходов. | + | *<tex>\delta</tex> {{---}} функция переходов. |
}} | }} | ||
| + | |||
| + | [[Изображение:PDAsmall.jpg|left|Рис. 1. Автомат с магазинной памятью]] | ||
| + | С ленты последовательно считываются символы входного алфавита (<tex>c_i</tex> {{---}} текущий считываемый символ). Символ <tex>x</tex> снимается с вершины стека. Вместо него помещается строка <tex>\alpha</tex> таким образом, чтобы первый символ строки находился на вершине стека. | ||
| + | |||
| + | Обычно под автоматом со стеком подразумевается недетерминированный автомат. Заметим, что [[Совпадение множества языков МП-автоматов и контекстно-свободных языков|недетерминированные автоматы со стеком эквивалентны по выразительной мощности контекстно свободным грамматикам.]] Если речь пойдет о [[Детерминированные автоматы с магазинной памятью|детерминированном автомате]], это будет указано отдельно. Заметим также, что [[Несовпадение класса языков, распознаваемых ДМП автоматами и произвольными МП автоматами|детерминированные и недетерминированные автоматы со стеком неэквивалентны]]. | ||
| + | <br style="clear:both" /> | ||
| + | |||
==Диаграммы переходов== | ==Диаграммы переходов== | ||
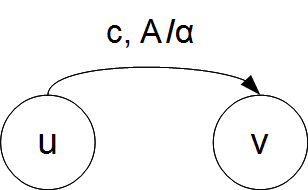
| − | <div class="tleft" style="clear:none">[[Файл:Transition1.png|thumb|Рис. 2. Переход: с - символ, прочитанный с ленты; A - символ, вынутый из стека; <tex>\alpha</tex> - строка, помещаемая в стек]]</div> | + | <div class="tleft" style="clear:none">[[Файл:Transition1.png|400px|thumb|Рис. 2. Переход: с {{---}} символ, прочитанный с ленты; A {{---}} символ, вынутый из стека; <tex>\alpha</tex> {{---}} строка, помещаемая в стек.]]</div> |
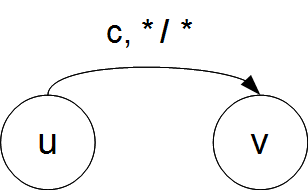
| − | <div class="tleft" style="clear:none">[[Файл:Transition2.png|thumb|Рис. 3. Переход по любому стековому символу, он же возвращается в стек]]</div> | + | <div class="tleft" style="clear:none">[[Файл:Transition2.png|400px|thumb|Рис. 3. Переход по любому стековому символу, он же возвращается в стек.]]</div> |
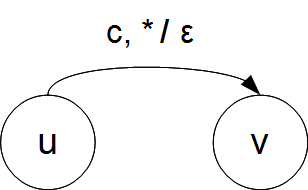
| − | <div class="tleft" style="clear:none">[[Файл:Transition3.png|thumb|Рис. 4. Переход по любому стековому символу, в стек кладется пустая строка]]</div> | + | <div class="tleft" style="clear:none">[[Файл:Transition3.png|400px|thumb|Рис. 4. Переход по любому стековому символу, в стек кладется пустая строка.]]</div> |
<br style="clear:both" /> | <br style="clear:both" /> | ||
| − | По соглашению маркер дна всегда находится на дне (за исключением случая, когда автомат является автоматом с допуском по пустому стеку). То есть, для <tex>\ | + | По соглашению маркер дна всегда находится на дне (за исключением случая, когда автомат является [[МП-автоматы, допуск по пустому стеку и по допускающему состоянию, эквивалентность|автоматом с допуском по пустому стеку]]). То есть, для <tex>\forall q \in Q,\forall c \in \Sigma \cup \{\varepsilon\} \Rightarrow \delta(q, c, z_0) \ni \langle p, \alpha \rangle </tex>, где <tex>p \in Q, \alpha \in \Gamma^*, \alpha = \alpha_1z_0</tex>. |
==Основные определения== | ==Основные определения== | ||
| − | |||
| − | |||
{{Определение | {{Определение | ||
| − | |definition= | + | |definition= |
| + | '''Мгновенное описание''' (англ. ''instantaneous descriptions'') {{---}} это набор <tex>\langle q, \alpha, \gamma \rangle</tex>, где <tex>q</tex> {{---}} текущее состояние, <tex>\alpha</tex> {{---}} остаток строки, <tex>\gamma</tex> {{---}} содержимое стека. | ||
}} | }} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | + | '''Переход за один шаг''' (англ. ''the "goes-to" relation'') обозначается как <tex>\langle q, \alpha, \gamma \rangle \vdash \langle r, \beta, \xi \rangle</tex>, где <tex>\alpha = c\beta</tex> (возможно, <tex>c=\varepsilon</tex>), <tex>\gamma = \chi\gamma', \xi = \eta\gamma'</tex>, <tex>\langle r, \eta \rangle \in \delta(q, c, \chi)</tex>. | |
| − | |||
| − | |||
| − | |||
}} | }} | ||
| + | {{Определение | ||
| + | |definition= '''Язык автомата с магазинной памятью''' (англ. ''language of a pushdown automaton'') <tex>L(A)=\{\alpha \mid \langle s, \alpha, z_0\rangle \vdash^* \langle t, \varepsilon, \gamma \rangle, t \in T\}</tex>. | ||
| + | }} | ||
| + | |||
| + | ==Пример недетерминированного МП-автомата== | ||
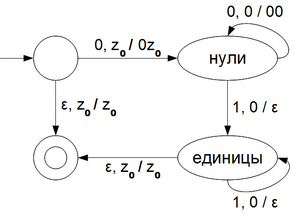
| + | [[Изображение:PDAexample.png|300px|thumb|left|Рис. 5. Недетерминированный МП-автомат для языка <tex>0^n1^n</tex>.]]<br style="clear:both" /> | ||
| + | |||
| + | == См. также == | ||
| + | * [[Детерминированные автоматы с магазинной памятью, допуск по пустому стеку]] | ||
| + | * [[ДМП-автоматы и неоднозначность]] | ||
| + | |||
| + | == Источники информации == | ||
| + | * ''Хопкрофт Д., Мотвани Р., Ульман Д.'' {{---}} '''Введение в теорию автоматов, языков и вычислений''', 2-е изд. : Пер. с англ. — Москва, Издательский дом «Вильямс», 2008. — 528 с. : ISBN 978-5-8459-1347-0 (рус.) | ||
| + | |||
| + | [[Категория: Теория формальных языков]] | ||
| + | [[Категория: Контекстно-свободные грамматики]] | ||
| + | [[Категория: МП-автоматы]] | ||
Текущая версия на 19:28, 4 сентября 2022
Содержание
Недетерминированный автомат с магазинной памятью
| Определение: |
Автомат с магазинной памятью (автомат со стеком, англ. pushdown automaton) — это набор , где
|
С ленты последовательно считываются символы входного алфавита ( — текущий считываемый символ). Символ снимается с вершины стека. Вместо него помещается строка таким образом, чтобы первый символ строки находился на вершине стека.
Обычно под автоматом со стеком подразумевается недетерминированный автомат. Заметим, что недетерминированные автоматы со стеком эквивалентны по выразительной мощности контекстно свободным грамматикам. Если речь пойдет о детерминированном автомате, это будет указано отдельно. Заметим также, что детерминированные и недетерминированные автоматы со стеком неэквивалентны.
Диаграммы переходов
По соглашению маркер дна всегда находится на дне (за исключением случая, когда автомат является автоматом с допуском по пустому стеку). То есть, для , где .
Основные определения
| Определение: |
| Мгновенное описание (англ. instantaneous descriptions) — это набор , где — текущее состояние, — остаток строки, — содержимое стека. |
| Определение: |
| Переход за один шаг (англ. the "goes-to" relation) обозначается как , где (возможно, ), , . |
| Определение: |
| Язык автомата с магазинной памятью (англ. language of a pushdown automaton) . |
Пример недетерминированного МП-автомата
См. также
- Детерминированные автоматы с магазинной памятью, допуск по пустому стеку
- ДМП-автоматы и неоднозначность
Источники информации
- Хопкрофт Д., Мотвани Р., Ульман Д. — Введение в теорию автоматов, языков и вычислений, 2-е изд. : Пер. с англ. — Москва, Издательский дом «Вильямс», 2008. — 528 с. : ISBN 978-5-8459-1347-0 (рус.)