Дополнительный, самодополнительный граф — различия между версиями
м (rollbackEdits.php mass rollback) |
|||
| (не показана 31 промежуточная версия 8 участников) | |||
| Строка 1: | Строка 1: | ||
| − | |||
| − | |||
== Дополнительный граф == | == Дополнительный граф == | ||
<wikitex> | <wikitex> | ||
{{Определение | {{Определение | ||
|definition = | |definition = | ||
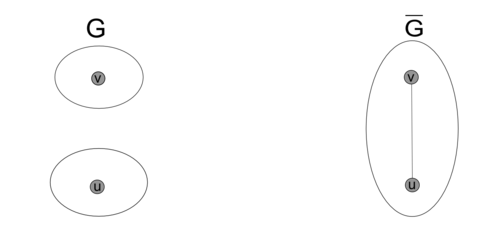
| − | Пусть дан граф | + | Пусть дан граф <tex>G \langle V, E \rangle</tex>. '''Дополнительным графом''' (англ. ''complement graph'') к $G$ называется граф <tex>G \langle V, \overline E \rangle</tex> то есть граф с вершинами из $V$ и теми и только теми ребрами из $E$, которые не вошли в $G$. |
}} | }} | ||
| + | {|class="wikitable" border="1" style="border-collapse:collapse; border:noborder" | ||
| + | |+ | ||
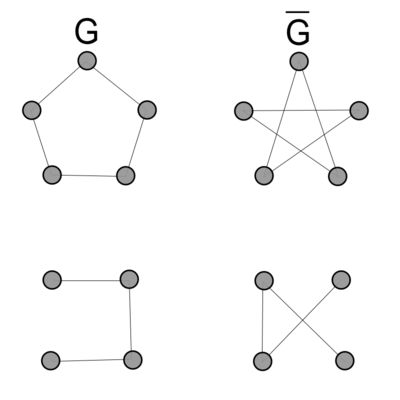
| + | |colspan="2"|Пример графа с 6-ю вершинами и его дополнение. | ||
| + | |- | ||
| + | | [[Файл:допграф1.png|200px|link=]] | ||
| + | | [[Файл:допграф2.png|200px|link=]] | ||
| + | |} | ||
| − | + | <br> | |
| − | + | <br> | |
| − | [[ | + | {{Теорема |
| + | |statement= | ||
| + | Дополнительный [[Основные_определения_теории_графов|граф]] к дополнительному графу $G$ есть граф $G$. | ||
| + | |proof= | ||
| + | <tex>\overline{\overline {G \langle V, E \rangle}} = \overline{G_1 \langle V, \overline{E} \rangle} = G_2 \langle V, \overline{\overline{E}} = G_2 \langle V, E \rangle = G</tex> | ||
| + | }} | ||
| + | <br><br> | ||
{{Теорема | {{Теорема | ||
|statement= | |statement= | ||
| − | + | В дополнительном графе к <tex>G \langle V, E \rangle</tex>. количество ребер равняется <tex dpi=150>\frac{\left\vert V \right\vert \cdot \left ( \left\vert V \right\vert - 1 \right )}{2} - \left\vert E \right\vert</tex>. | |
|proof= | |proof= | ||
| − | $ | + | Так как множества ребер в $G$ и $\overline{G}$ дизъюнктны, то $\left\vert E \right\vert + \left\vert \overline{E} \right\vert =$ <tex dpi=150>\frac{\left\vert V \right\vert \cdot \left ( \left\vert V \right\vert - 1 \right )}{2}</tex>, из чего следует утверждение теоремы. |
}} | }} | ||
| + | |||
| + | <br><br> | ||
{{Теорема | {{Теорема | ||
|statement= | |statement= | ||
| − | Дополнительный граф к несвязному графу связен. | + | Дополнительный граф к [[Отношение связности, компоненты связности|несвязному]] графу связен. |
|proof= | |proof= | ||
Для графа с одной вершиной утверждение очевидно. Докажем его для остальных графов. | Для графа с одной вершиной утверждение очевидно. Докажем его для остальных графов. | ||
| − | Пусть $G$ - данный граф. Рассмотрим произвольные вершины $v$ и $u$ из $G$. Возможны два случая. | + | Пусть $G$ {{---}} данный граф. Рассмотрим произвольные вершины $v$ и $u$ из $G$. Возможны два случая: $v$ и $u$ лежат в одной или в разных компонентах связности. |
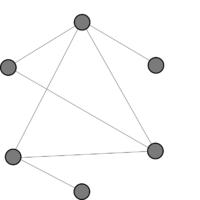
| − | *$v$ и $u$ лежат в разных компонентах связности $G$. | + | *Пусть $v$ и $u$ лежат в разных компонентах связности $G$. |
| − | Тогда ребро $(u, v) \notin G \Rightarrow (u, v) \in \overline{G} \Rightarrow u$ и $v$ лежат в одной компоненте связности $\overline{G}$. | + | :Тогда ребро $(u, v) \notin G \Rightarrow (u, v) \in \overline{G} \Rightarrow u$ и $v$ лежат в одной компоненте связности $\overline{G}$. |
<br> | <br> | ||
| − | [[Файл: | + | [[Файл:допграф3.png|500px|слева]] |
| − | <br><br><br><br><br><br> | + | <br><br><br><br><br><br><br><br><br><br><br><br><br><br><br> |
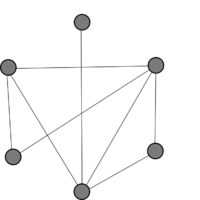
| − | *$v$ и $u$ лежат в | + | *Пусть $v$ и $u$ лежат в одной компоненте связности $G$. |
$G$ {{---}} несвязный $\Rightarrow \exists w \in G$, не лежащая в одной компоненте связности с $v$ и $u$. | $G$ {{---}} несвязный $\Rightarrow \exists w \in G$, не лежащая в одной компоненте связности с $v$ и $u$. | ||
| − | Тогда по предыдущему пункту $(v, w) \in \overline{G}$ и $(u, w) \in \overline{G} \Rightarrow v$ и $u$ лежат в одной компоненте связности $\overline{G}$. | + | :Тогда по предыдущему пункту $(v, w) \in \overline{G}$ и $(u, w) \in \overline{G} \Rightarrow v$ и $u$ лежат в одной компоненте связности $\overline{G}$. |
<br> | <br> | ||
| − | [[Файл: | + | [[Файл:допграф4.png|500px|слева]] |
| − | <br><br><br><br><br><br> | + | <br><br><br><br><br><br><br><br><br><br><br><br><br><br><br> |
| + | |||
| + | |||
| + | То есть $\forall u, v \in V$ $u$ и $v$ лежат в одной компоненте связности $\overline{G}$, то есть $\overline{G}$ связен. | ||
| + | }} | ||
| + | |||
| + | == Самодополнительный граф == | ||
| + | |||
| + | {{Определение | ||
| + | |definition = | ||
| + | '''Самодополнительным графом''' (англ. ''self-complement'') называется граф, [[Основные определения теории графов|изоморфный]] своему дополнительному. | ||
| + | }} | ||
| + | <br> | ||
| + | <br> | ||
| + | {{Теорема | ||
| + | |statement= | ||
| + | Любой самодополнительный граф имеет $4k$ или $4k + 1$ вершину. | ||
| + | |proof= | ||
| + | |||
| + | Обозначим $\left\vert V \right\vert$ за $n$, $\left\vert E \right\vert$ за $a$. | ||
| + | Граф самодополнителен $\Rightarrow$ количество его ребер равно количеству ребер в его дополнении. | ||
| + | |||
| + | Но по одной из предыдущих теорем, <tex dpi=150>\frac{n \cdot \left ( n - 1 \right )}{2}</tex> $- a = \left\vert \overline{E} \right\vert = a \Rightarrow 4a = n \cdot \left ( n - 1 \right )$, из чего следует утверждение теоремы. | ||
| − | |||
}} | }} | ||
| + | <br><br> | ||
| + | |||
| + | {{Теорема | ||
| + | |statement= | ||
| + | Для любых $k > 0$ существует самодополнительный граф с $4k$ или $4k + 1$ вершиной. | ||
| + | |proof= | ||
| + | |||
| + | Будем доказывать по индукции. Для $k = 1$ утверждение справедливо. | ||
| + | |||
| + | [[Файл:допграф7.png|400px|link=]] | ||
| + | |||
| + | Пусть у нас есть самодополнительный граф $G$ с $n$ вершинами, построим самодополнительный граф с $n + 4$ вершинами. | ||
| + | Добавим к $G$ 4 вершины $v_1, v_2, v_3, v_4$ и ребра: | ||
| + | |||
| + | *Добавим ребра $(v_1, v_2), (v_2, v_3), (v_3, v_4)$ | ||
| + | *Если $u$ была вершиной в $G$, добавим ребра $(u, v_1), (u, v_4)$ | ||
| + | |||
| + | Назовем полученный граф $A$. Докажем, что $A$ самодополнителен. | ||
| + | |||
| + | Рассмотрим биекцию на множестве вершин $A$ и $\overline{A}$: | ||
| + | *Среди всех вершин, принадлежавших $G$ биекция будет такая же, как и у $G$ с $\overline{G}$; | ||
| + | *$v_1 \rightarrow v_2, v_2 \rightarrow v_4, v_3 \rightarrow v_1, v_4 \rightarrow v_3$. | ||
| + | |||
| + | Тогда между ребрами $A$ и $\overline{A}$ тоже будет биекция. | ||
| + | [[Файл:допграф9.png|400px|]] | ||
| + | }} | ||
</wikitex> | </wikitex> | ||
| + | |||
| + | == См. также == | ||
| + | * [[Основные определения теории графов]] | ||
| + | * [[Отношение связности, компоненты связности]] | ||
| + | |||
| + | == Источники информации == | ||
| + | * ''Харари Ф.'' Теория графов. /пер. с англ. — изд. 2-е — М.: Едиториал УРСС, 2003. — 296 с. — ISBN 5-354-00301-6 | ||
| + | * [https://ru.wikipedia.org/wiki/Дополнение_графа Википедия {{---}} дополнение графа] | ||
| + | * [https://ru.wikipedia.org/wiki//Самодополнительный_граф Википедия {{---}} самодополнительный граф] | ||
| + | |||
[[Категория: Алгоритмы и структуры данных]] | [[Категория: Алгоритмы и структуры данных]] | ||
[[Категория: Основные определения теории графов]] | [[Категория: Основные определения теории графов]] | ||
Текущая версия на 19:35, 4 сентября 2022
Дополнительный граф
<wikitex>
| Определение: |
| Пусть дан граф . Дополнительным графом (англ. complement graph) к $G$ называется граф то есть граф с вершинами из $V$ и теми и только теми ребрами из $E$, которые не вошли в $G$. |
| Пример графа с 6-ю вершинами и его дополнение. | |
|
|
| Теорема: |
Дополнительный граф к дополнительному графу $G$ есть граф $G$. |
| Доказательство: |
| Теорема: |
В дополнительном графе к . количество ребер равняется . |
| Доказательство: |
| Так как множества ребер в $G$ и $\overline{G}$ дизъюнктны, то $\left\vert E \right\vert + \left\vert \overline{E} \right\vert =$ , из чего следует утверждение теоремы. |
| Теорема: |
Дополнительный граф к несвязному графу связен. |
| Доказательство: |
|
Для графа с одной вершиной утверждение очевидно. Докажем его для остальных графов. Пусть $G$ — данный граф. Рассмотрим произвольные вершины $v$ и $u$ из $G$. Возможны два случая: $v$ и $u$ лежат в одной или в разных компонентах связности.
$G$ — несвязный $\Rightarrow \exists w \in G$, не лежащая в одной компоненте связности с $v$ и $u$.
|
Самодополнительный граф
| Определение: |
| Самодополнительным графом (англ. self-complement) называется граф, изоморфный своему дополнительному. |
| Теорема: |
Любой самодополнительный граф имеет $4k$ или $4k + 1$ вершину. |
| Доказательство: |
|
Обозначим $\left\vert V \right\vert$ за $n$, $\left\vert E \right\vert$ за $a$. Граф самодополнителен $\Rightarrow$ количество его ребер равно количеству ребер в его дополнении. Но по одной из предыдущих теорем, $- a = \left\vert \overline{E} \right\vert = a \Rightarrow 4a = n \cdot \left ( n - 1 \right )$, из чего следует утверждение теоремы. |
</wikitex>
См. также
Источники информации
- Харари Ф. Теория графов. /пер. с англ. — изд. 2-е — М.: Едиториал УРСС, 2003. — 296 с. — ISBN 5-354-00301-6
- Википедия — дополнение графа
- Википедия — самодополнительный граф