Матрица Кирхгофа — различия между версиями
Ak57 (обсуждение | вклад) м |
м (rollbackEdits.php mass rollback) |
||
| (не показано 10 промежуточных версий 3 участников) | |||
| Строка 1: | Строка 1: | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | '''Матрицей Кирхгофа''' [ | + | '''Матрицей Кирхгофа''' [[Основные определения теории графов#def_simple_graph|простого графа]] <tex>G = (V,E) </tex> называется матрица <tex> K (|V| \times |V|) = \parallel k_{i,j} \parallel </tex>, элементы которой определяются равенством: <tex> |
k_{i,j} = | k_{i,j} = | ||
\begin{cases} | \begin{cases} | ||
| Строка 10: | Строка 10: | ||
</tex> | </tex> | ||
}} | }} | ||
| − | Иными словами, на главной диагонали матрицы Кирхгофа находятся степени вершин, а на пересечении <tex>i</tex>-й строки и <tex>j</tex>-го столбца (<tex>i \ne j</tex>) стоит -1, если вершины с номерами <tex>i</tex> и <tex>j</tex> смежны, и 0 в противном случае. | + | Иными словами, на главной диагонали матрицы Кирхгофа находятся степени вершин, а на пересечении <tex>i</tex>-й строки и <tex>j</tex>-го столбца (<tex>i \ne j</tex>) стоит <tex>-1</tex>, если вершины с номерами <tex>i</tex> и <tex>j</tex> смежны, и <tex>0</tex> в противном случае. |
== Пример матрицы Кирхгофа== | == Пример матрицы Кирхгофа== | ||
| + | |||
{|class="wikitable" | {|class="wikitable" | ||
!Граф | !Граф | ||
| Строка 30: | Строка 31: | ||
== Некоторые свойства == | == Некоторые свойства == | ||
| − | + | {{Утверждение | |
| + | |statement=Сумма элементов каждой строки (столбца) матрицы Кирхгофа равна нулю: | ||
| + | : <tex>\ \sum_{i=1}^{|V|} k_{i,j} = 0</tex>. | ||
| + | }} | ||
| + | |||
| + | {{Утверждение | ||
| + | |statement=Определитель матрицы Кирхгофа равен нулю: | ||
| + | : <tex>\det K=0</tex> | ||
| + | |proof=<tex> \det K = | ||
| + | \begin{vmatrix} | ||
| + | k_{1, 1} & k_{1, 2} & \cdots & k_{1, |V|} \\ | ||
| + | k_{2, 1} & k_{2, 2} & \cdots & k_{2, |V|} \\ | ||
| + | \vdots & \vdots & \ddots & \vdots \\ | ||
| + | k_{|V|, 1} & k_{|V|, 2} & \cdots & k_{|V|, |V|} | ||
| + | \end{vmatrix} | ||
| + | </tex> | ||
| − | + | Прибавим к первой строке все остальные строки (это не изменит значение определителя): | |
| − | <tex> K = | + | <tex>\begin{vmatrix} |
| + | k_{1, 1} + k_{2, 1} + \cdots + k_{|V|, 1} & k_{1, 2} + k_{2, 2} + \cdots + k_{|V|, 2} & \cdots & k_{1, |V|} + k_{2, |V|} + \cdots + k_{|V|, |V|} \\ | ||
| + | k_{2, 1} & k_{2, 2} & \cdots & k_{2, |V|} \\ | ||
| + | \vdots & \vdots & \ddots & \vdots \\ | ||
| + | k_{|V|, 1} & k_{|V|, 2} & \cdots & k_{|V|, |V|} | ||
| + | \end{vmatrix} | ||
| + | </tex> | ||
| + | |||
| + | Так как сумма элементов каждого столбца равна <tex>0</tex>, получим: | ||
| + | |||
| + | <tex>\det K = \begin{vmatrix} | ||
| + | 0 & 0 & \cdots & 0 \\ | ||
| + | k_{2, 1} & k_{2, 2} & \cdots & k_{2, |V|} \\ | ||
| + | \vdots & \vdots & \ddots & \vdots \\ | ||
| + | k_{|V|, 1} & k_{|V|, 2} & \cdots & k_{|V|, |V|} | ||
| + | \end{vmatrix} = 0 | ||
| + | </tex> | ||
| + | }} | ||
| + | |||
| + | {{Утверждение | ||
| + | |statement=Матрица Кирхгофа простого графа симметрична: | ||
| + | : <tex>\ k_{i,j} = k_{j,i}\quad i,j=1, \ldots, |V|</tex>. | ||
| + | }} | ||
| + | |||
| + | {{Утверждение | ||
| + | |statement=Связь с [[Матрица смежности графа|матрицей смежности]]: | ||
| + | :<tex> K = | ||
\begin{pmatrix} | \begin{pmatrix} | ||
| − | deg(v_1) & 0 & \cdots & 0 \\ | + | \mathrm{deg}(v_1) & 0 & \cdots & 0 \\ |
| − | 0 & deg(v_2) & \cdots & 0 \\ | + | 0 & \mathrm{deg}(v_2) & \cdots & 0 \\ |
\vdots & \vdots & \ddots & \vdots \\ | \vdots & \vdots & \ddots & \vdots \\ | ||
| − | 0 & 0 & \cdots & deg(v_n) | + | 0 & 0 & \cdots & \mathrm{deg}(v_n) |
\end{pmatrix} - A, | \end{pmatrix} - A, | ||
</tex> | </tex> | ||
| + | где <tex>A</tex> — матрица смежности графа <tex>G</tex>. | ||
| + | }} | ||
| − | где <tex> | + | {{Утверждение |
| + | |statement=[[Связь матрицы Кирхгофа и матрицы инцидентности|Связь с матрицей инцидентности]]: | ||
| + | :<tex> K = I \cdot I^T, </tex> где <tex>I</tex> — матрица инцидентности некоторой ориентации графа. | ||
| + | }} | ||
| + | |||
| + | {{Утверждение | ||
| + | |statement=<tex>0</tex> является [[Собственные векторы и собственные значения|собственным значением]] матрицы, кратность его равна числу [[Отношение связности, компоненты связности|компонент связности]] графа. | ||
| + | |proof=Собственным значением матрицы называют значения <tex>\lambda</tex>, которые удовлетворяют уравнению: | ||
| + | |||
| + | <tex>\begin{vmatrix} | ||
| + | k_{1, 1} - \lambda &k_{1, 2} & \cdots & k_{1, |V|} \\ | ||
| + | k_{2, 1} & k_{2, 2} - \lambda & \cdots & k_{2, |V|} \\ | ||
| + | \vdots & \vdots & \ddots & \vdots \\ | ||
| + | k_{|V|, 1} & k_{|V|, 2} & \cdots & k_{|V|, |V| - \lambda} | ||
| + | \end{vmatrix} = 0 | ||
| + | </tex> | ||
| + | |||
| + | Прибавим к первой строке все остальные строки (это не изменит значение определителя): | ||
| + | |||
| + | <tex>\begin{vmatrix} | ||
| + | k_{1, 1} + k_{2, 1} + \cdots + k_{|V|, 1} - \lambda & k_{1, 2} + k_{2, 2} + \cdots + k_{|V|, 2} - \lambda & \cdots & k_{1, |V|} + k_{2, |V|} + \cdots + k_{|V|, |V|} - \lambda \\ | ||
| + | k_{2, 1} & k_{2, 2} - \lambda & \cdots & k_{2, |V|} \\ | ||
| + | \vdots & \vdots & \ddots & \vdots \\ | ||
| + | k_{|V|, 1} & k_{|V|, 2} & \cdots & k_{|V|, |V|} - \lambda | ||
| + | \end{vmatrix} | ||
| + | </tex> | ||
| + | |||
| + | Так как сумма элементов каждого столбца равна <tex>0</tex>, получим: | ||
| + | |||
| + | <tex>\begin{vmatrix} | ||
| + | - \lambda &-\lambda & \cdots & - \lambda \\ | ||
| + | k_{2, 1} & k_{2, 2} - \lambda & \cdots & k_{2, |V|} \\ | ||
| + | \vdots & \vdots & \ddots & \vdots \\ | ||
| + | k_{|V|, 1} & k_{|V|, 2} & \cdots & k_{|V|, |V|} - \lambda | ||
| + | \end{vmatrix} = 0 | ||
| + | </tex> | ||
| + | |||
| + | <tex>- \lambda | ||
| + | \begin{vmatrix} | ||
| + | 1 & 1 & \cdots & 1 \\ | ||
| + | k_{2, 1} & k_{2, 2} - \lambda & \cdots & k_{2, |V|} \\ | ||
| + | \vdots & \vdots & \ddots & \vdots \\ | ||
| + | k_{|V|, 1} & k_{|V|, 2} & \cdots & k_{|V|, |V|} - \lambda | ||
| + | \end{vmatrix}= 0. | ||
| + | </tex> | ||
| + | |||
| + | Следовательно, <tex>0</tex> является собственным значением. | ||
| + | |||
| + | '''Доказательство кратности:''' | ||
| + | |||
| + | Пусть дан граф <tex>G</tex> c <tex>n</tex> компонентами связности. Перенумеруем его вершины так, чтобы сначала шли вершины первой компоненты связности, затем второй и т.д. Тогда матрица Кирхгофа примет блочно-диагональный вид, и <tex>i</tex>-тый блок этой матрицы будет являтся матрицей Кирхгофа для <tex>i</tex>-той компоненты связности. | ||
| + | |||
| + | Из свойства блочно-диагональной матрицы <tex>\det K = \det K_{1} \cdot \det K_{2} \cdot \ldots \cdot \det K_{n}</tex>, где <tex>K_{i}</tex> — матрица Кирхгофа для <tex>i</tex>-той компоненты связности, и свойства, доказанного выше, | ||
| + | |||
| + | <tex>\det K_{i} = - \lambda \cdot det X_{i} \quad \Rightarrow \quad \det K = (-1)^{n} \cdot \lambda^{n} \cdot \det X_{1} \cdot \det X_{2} \cdot \ldots \cdot \det X_{n}</tex> | ||
| + | }} | ||
| + | |||
| + | ==См. также== | ||
| − | + | *[[Связь матрицы Кирхгофа и матрицы инцидентности]] | |
| + | *[[Подсчет числа остовных деревьев с помощью матрицы Кирхгофа]] | ||
| − | ==Источники== | + | ==Источники информации== |
| − | + | *Асанов М., Баранский В., Расин В.: Дискретная математика: Графы, матроиды, алгоритмы. стр. 18 | |
| − | [http://ru.wikipedia.org/wiki/%CC%E0%F2%F0%E8%F6%E0_%CA%E8%F0%F5%E3%EE%F4%E0 Википедия | + | *[http://ru.wikipedia.org/wiki/%CC%E0%F2%F0%E8%F6%E0_%CA%E8%F0%F5%E3%EE%F4%E0 Википедия — Матрица Кирхгофа] |
[[Категория: Алгоритмы и структуры данных]] | [[Категория: Алгоритмы и структуры данных]] | ||
| − | [[Категория: Остовные деревья ]] | + | [[Категория: Остовные деревья]] |
| + | [[Категория: Свойства остовных деревьев ]] | ||
Текущая версия на 19:12, 4 сентября 2022
| Определение: |
| Матрицей Кирхгофа простого графа называется матрица , элементы которой определяются равенством: |
Иными словами, на главной диагонали матрицы Кирхгофа находятся степени вершин, а на пересечении -й строки и -го столбца () стоит , если вершины с номерами и смежны, и в противном случае.
Пример матрицы Кирхгофа
| Граф | Матрица Кирхгофа |
|---|---|
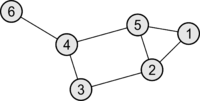
|
Некоторые свойства
| Утверждение: |
Сумма элементов каждой строки (столбца) матрицы Кирхгофа равна нулю:
|
| Утверждение: |
Определитель матрицы Кирхгофа равен нулю:
|
|
Прибавим к первой строке все остальные строки (это не изменит значение определителя):
Так как сумма элементов каждого столбца равна , получим: |
| Утверждение: |
Матрица Кирхгофа простого графа симметрична:
|
| Утверждение: |
Связь с матрицей смежности:
|
| Утверждение: |
Связь с матрицей инцидентности:
|
| Утверждение: |
является собственным значением матрицы, кратность его равна числу компонент связности графа. |
|
Собственным значением матрицы называют значения , которые удовлетворяют уравнению:
Прибавим к первой строке все остальные строки (это не изменит значение определителя):
Так как сумма элементов каждого столбца равна , получим:
Следовательно, является собственным значением. Доказательство кратности: Пусть дан граф c компонентами связности. Перенумеруем его вершины так, чтобы сначала шли вершины первой компоненты связности, затем второй и т.д. Тогда матрица Кирхгофа примет блочно-диагональный вид, и -тый блок этой матрицы будет являтся матрицей Кирхгофа для -той компоненты связности. Из свойства блочно-диагональной матрицы , где — матрица Кирхгофа для -той компоненты связности, и свойства, доказанного выше, |
См. также
- Связь матрицы Кирхгофа и матрицы инцидентности
- Подсчет числа остовных деревьев с помощью матрицы Кирхгофа
Источники информации
- Асанов М., Баранский В., Расин В.: Дискретная математика: Графы, матроиды, алгоритмы. стр. 18
- Википедия — Матрица Кирхгофа