Персистентные структуры данных — различия между версиями
(→Преобразование списка в персистентный за O(1)) |
м (rollbackEdits.php mass rollback) |
||
| (не показана 121 промежуточная версия 15 участников) | |||
| Строка 1: | Строка 1: | ||
| − | |||
{{Определение | {{Определение | ||
| − | |definition= | + | |definition= '''Персистентные структуры данных''' (англ. ''persistent data structure'') — это структуры данных, которые при внесении в них каких-то изменений сохраняют все свои предыдущие состояния и доступ к этим состояниям.}} |
==Уровни персистентности== | ==Уровни персистентности== | ||
| − | Есть несколько уровней персистентности | + | Есть несколько уровней персистентности: |
| − | *частичная (англ. ''partial'') | + | *частичная (англ. ''partial''), |
| − | *полная (англ. ''full'') | + | *полная (англ. ''full''), |
| − | *конфлюэнтная (англ. ''confluent'') | + | *конфлюэнтная (англ. ''confluent''), |
| − | * | + | *функциональная (англ. ''functional''). |
В частично персистентных структурах данных к каждой версии можно делать запросы, но изменять можно только последнюю версию структуры данных. | В частично персистентных структурах данных к каждой версии можно делать запросы, но изменять можно только последнюю версию структуры данных. | ||
| Строка 14: | Строка 13: | ||
В полностью персистентных структурах данных можно менять не только последнюю, но и любую версию структур данных, также к любой версии можно делать запросы. | В полностью персистентных структурах данных можно менять не только последнюю, но и любую версию структур данных, также к любой версии можно делать запросы. | ||
| − | Конфлюэнтные | + | Конфлюэнтные структуры данных позволяют объединять две структуры данных в одну (деревья поиска, которые можно сливать). |
Функциональные структуры данных полностью персистентны по определению, так как в них запрещаются уничтожающие присваивания, т.е. любой переменной значение может быть присвоено только один раз и изменять значения переменных нельзя. | Функциональные структуры данных полностью персистентны по определению, так как в них запрещаются уничтожающие присваивания, т.е. любой переменной значение может быть присвоено только один раз и изменять значения переменных нельзя. | ||
| Строка 21: | Строка 20: | ||
==Способы преобразования структур данных в персистентные== | ==Способы преобразования структур данных в персистентные== | ||
Есть несколько способов сделать любую структуру персистентной: | Есть несколько способов сделать любую структуру персистентной: | ||
| − | *полное копирование (англ. ''full copy'') когда при любой операции изменения полностью копируется структура данных и в получившуюся новую копию вносятся изменения | + | *полное копирование (англ. ''full copy'') когда при любой операции изменения полностью копируется структура данных и в получившуюся новую копию вносятся изменения, |
| − | * копирование пути (англ. ''path | + | * копирование пути (англ. ''path copying''), |
*метод «толстых» узлов (англ. ''fat node''). | *метод «толстых» узлов (англ. ''fat node''). | ||
| − | Рассмотрим для начала частичную персистентность. Для наглядности занумеруем разные версии структур данных. История изменений структуры данных линейна, | + | Рассмотрим для начала частичную персистентность. Для наглядности занумеруем разные версии структур данных. История изменений структуры данных линейна, в любой момент времени можно обратиться к любой версии структуры данных, но поменять возможно только последнюю версию (на рисунке она выделена синим цветом). |
[[Файл:Список версий.png]] | [[Файл:Список версий.png]] | ||
| − | Сформулируем, что такое структура данных. | + | Сформулируем, что такое структура данных. В нашем понимании структурой данных будет называться набор узлов, в которых хранятся какие-то данные, и эти узлы связаны ссылками. Пример структуры данных — [[Дерево поиска, наивная реализация|дерево]]. Рассмотрим, как методом копирования пути превратить дерево в персистентное. |
===Метод копирование пути=== | ===Метод копирование пути=== | ||
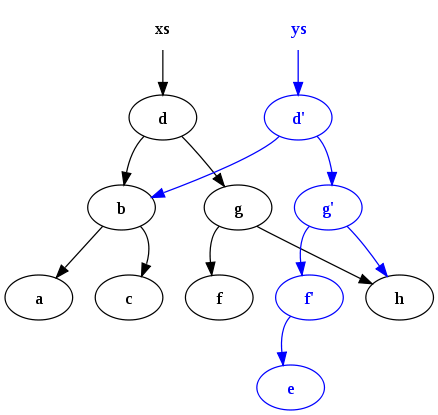
| − | Пусть | + | Пусть есть [[АВЛ-дерево |сбалансированное дерево поиска]]. Все операции в нем делаются за <tex>O(h)</tex>, где <tex>h</tex> — высота дерева, а высота дерева <tex>O</tex> <tex>(\log n)</tex>, где <tex>n</tex> — количество вершин. Пусть необходимо сделать какое-то обновление в этом сбалансированном дереве, например, добавить очередной элемент, но при этом нужно не потерять старое дерево. Возьмем узел, в который нужно добавить нового ребенка. Вместо того чтобы добавлять нового ребенка, скопируем этот узел, к копии добавим нового ребенка, также скопируем все узлы вплоть до корня, из которых достижим первый скопированный узел вместе со всеми указателями. Все вершины, из которых измененный узел не достижим, мы не трогаем. Количество новых узлов всегда будет порядка логарифма. В результате имеем доступ к обеим версиям дерева. |
| − | [[Файл:Копирование пути.png]] | + | [[Файл:Копирование пути.png]] |
| + | |||
| + | Так как рассматривается сбалансированное дерево поиска, то поднимая вершину вверх при балансировке, нужно делать копии всех вершин, участвующих во вращениях, у которых изменились ссылки на детей. Таких всегда не более трех, поэтому ассимптотика <tex>O</tex> <tex>( \log n)</tex> не пострадает. Когда балансировка закончится, нужно дойти вверх до корня, делая копии вершин на пути. | ||
| + | |||
| + | Этот метод хорошо работает на [[Стек|стеке]], двоичных ([[Декартово дерево |декартовых]], [[Красно- черное дерево | красно-черных]]) деревьях. Но в случае преобразования [[Очередь| очереди]] в персистентную операция добавления будет очень дорогой, так как элемент добавляется в хвост очереди, который достижим из всех остальных элементов. Также не выгодно применять этот метод и в случае, когда в структуре данных имеются ссылки на родителя. | ||
| + | |||
| + | ==== Реализация на основе дерева отрезков ==== | ||
| + | |||
| + | На основе дерева отрезков можно построить полностью персистентную структуру данных. | ||
| + | |||
| + | Для реализации персистентного дерева отрезков удобно несколько изменить структуру дерева. Для этого будем использовать явные указатели <tex>L</tex> и <tex>R</tex> для дочерних элементов. Кроме того, заведем массив <tex>roots[]</tex>, в котором <tex>roots[i]</tex> указывает на корень дерева отрезков версии <tex>i</tex> | ||
| + | |||
| + | Для построения персистентного дерева отрезков из <tex>n</tex> элементов необходимо применить <tex>n</tex> раз операцию добавления элемента к последней версии дерева. Для того, чтобы добавить новый элемент к <tex>k</tex>-ой версии дерева, необходимо проверить, является ли оно полным бинарным. Если да, то создадим новый корень, левым сыном сделаем <tex>roots[k]</tex>. Иначе, сделаем копию корня исходной версии. Добавим корень в конец массива корней. Далее, спускаясь от корня к первому свободному листу, будем создавать несуществующие узлы и клонировать существующие. После этого в новой ветке необходимо обновить значение функции и некоторые указатели дочерних элементов. Поэтому, возвращаясь из рекурсии, будем менять один указатель на только что созданную или скопированную вершину, а также обновим значение функции, для которой строилось дерево. После этой операции в дереве появится новая версия, содержащая вставленный элемент. | ||
| + | |||
| + | Для того, чтобы изменить элемент в персистентном дереве отрезков, необходимо сделать следующие действия: спустимся в дереве от корня нужной версии до требуемого элемента, скопируем его, изменим значение, и, поднимаясь по дереву, будем клонировать узлы. При этом необходимо менять указатель на одного из детей на узел, созданный при предыдущем клонировании. После копирования корня, добавим новый корень в конец массива корней. | ||
| + | |||
| + | [[Файл:persist.png]] | ||
| + | |||
| + | Здесь изображено персистентное дерево отрезков с операцией минимум, в котором изначально было 3 вершины. Сперва к нему была добавлена вершина со значением 2, а потом изменена вершина со значением 7. Цвет ребер и вершин соответствует времени их появления. Синий цвет элементов означает, что они были изначально, зеленый - что они появились после добавления, а оранжевый - что они появились после изменения элемента. | ||
===Метод «толстых» узлов=== | ===Метод «толстых» узлов=== | ||
| − | Пусть в структуре данных есть узел, в котором нужно сделать изменения (например, на | + | Пусть в структуре данных есть узел, в котором нужно сделать изменения (например, на рисунке ниже в первой версии структуры данных в узле <tex>X</tex> есть поле <tex>a=3</tex>, а во второй версии это поле должно быть равно <tex>4</tex>), но при этом нужно сохранить доступ к старой версии узла <tex>X</tex> и не нужно экономить время. В таком случае можно хранить обе версии узла <tex>X</tex> в большом комбинированном узле. |
| − | [[Файл:Метод толстых узлов.png| | + | |
| + | [[Файл:Метод толстых узлов.png|600px|центр]] | ||
| + | |||
| + | В примере выше в этом «толстом» узле будет храниться первая версия <tex>V_1</tex>, у которой <tex>a=3</tex> и вторая версия <tex>V_2</tex>, у которой <tex>a=4</tex>. Если далее последуют еще какие-то изменения (например, поле <tex>b</tex> узла <tex>X</tex> станет равно <tex>5</tex>) добавим в толстый узел <tex>X</tex> еще одну версию — <tex>V_3</tex>. | ||
| − | + | [[Файл:Список версий1.png|500px|центр]] | |
| − | Чтобы быстро найти нужную версию в списке версий, хранящихся в «толстом» узле, нужно хранить их в виде дерева. Тогда мы сможем за логарифм найти нужную версию и к ней обратиться. Значит все операции, которые будут производиться на этой структуре данных, будут домножаться на логарифм от числа версий. | + | |
| + | Пусть нужно сделать запрос ко второй версии структуры данных (на рисунке выше это запрос <tex>X.a-?)</tex>. Чтобы сделать этот запрос, нужно зайти в узел <tex>X</tex> и найти в списке версий максимальную версию, которая меньше или равна версии запроса (в примере на рисунке это версия <tex>2</tex>), и в этой версии узла найти значение поля <tex>a</tex> (в примере <tex>a=4</tex>). | ||
| + | Чтобы быстро найти нужную версию в списке версий, хранящихся в «толстом» узле, нужно хранить их в виде дерева. Тогда мы сможем за логарифм найти нужную версию и к ней обратиться. Значит, все операции, которые будут производиться на этой структуре данных, будут домножаться на логарифм от числа версий. | ||
| + | |||
| + | Структура толстого узла может быть и другой: к каждой вершине можно хранить лог ее изменений, в который записывается версия, в которой произошло изменение, а также само изменение. Такая структура толстого узла рассмотрена ниже, в разделах об общих методах получения частично и полностью персистентных структур данных. Лог может быть организован по-разному. Обычно делают отдельный лог для каждого поля вершины. Когда что-то меняется в вершине, то в лог соответствующего поля записывается это изменение и номер версии, с которой данное изменение произошло. Когда нужно обратиться к старой версии, то двоичным поиском ищут в логе последнее изменение до этой версии и находят нужное значение. | ||
| + | Метод ''fat node'' дает замедление <tex> \log t</tex>, где <tex>t</tex> — число изменений структуры данных; памяти требуется <tex>n+t</tex>, где <tex>n</tex> — число вершин в структуре данных. | ||
==Преобразование списка в персистентный за O(1)== | ==Преобразование списка в персистентный за O(1)== | ||
| − | Если скомбинировать методы ''path copiyng'' и ''fat node'', то получим универсальный метод, который позволит преобразовывать структуры данных в частично персистентные без дополнительного логарифма памяти. | + | Если скомбинировать методы ''path copiyng'' и ''fat node'', то получим универсальный метод, который позволит преобразовывать структуры данных в частично персистентные без дополнительного логарифма памяти и времени. |
| − | Пусть мы имеем [[Список| двусвязный список]] и хотим внести в него какое-то изменение, например, добавить узел <tex>Z</tex> между узлами <tex>X</tex> и <tex>Y</tex>, то есть при переходе из версии <tex>1</tex> в версию <tex>2</tex> добавим в | + | Пусть мы имеем [[Список| двусвязный список]] и хотим внести в него какое-то изменение, например, добавить узел <tex>Z</tex> между узлами <tex>X</tex> и <tex>Y</tex>, то есть при переходе из версии <tex>1</tex> в версию <tex>2</tex> добавим в двусвязный список узел <tex>Z</tex>. |
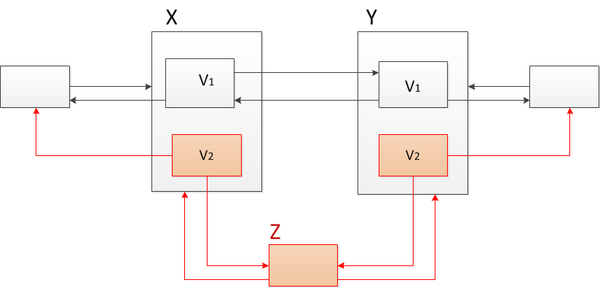
Применим метод «толстых» узлов. Для этого в узлы <tex>X</tex> и <tex>Y</tex> добавим вторую версию и изменим ссылку, следующую из <tex>X</tex>, и предыдущую перед <tex>Y</tex>, как показано на рисунке. | Применим метод «толстых» узлов. Для этого в узлы <tex>X</tex> и <tex>Y</tex> добавим вторую версию и изменим ссылку, следующую из <tex>X</tex>, и предыдущую перед <tex>Y</tex>, как показано на рисунке. | ||
| − | + | Этот алгоритм работает следующим образом. Например, текущая первая версия. Идем по списку слева направо от первого узла к узлу <tex>X</tex>, а затем нужно перейти к следующему узлу. В «толстом» узле <tex>X</tex> выбираем нужную (первую) версию и далее следуем по ссылкам. | |
| − | [[Файл:Список1.png| | + | [[Файл:Список1.png|600px]] |
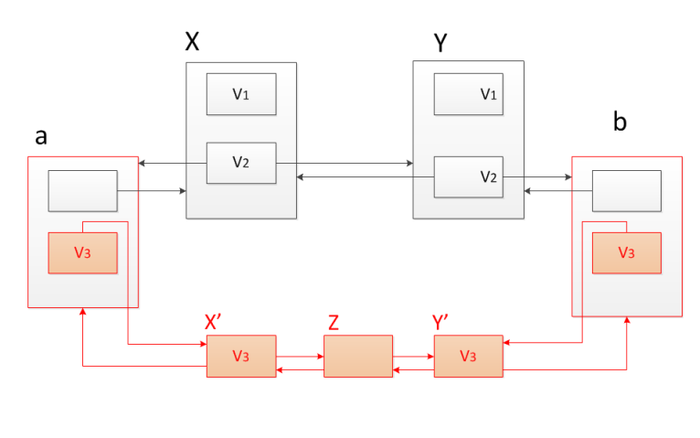
| − | Пусть мы хотим добавить еще один элемент между узлами <tex>X</tex> и <tex>Y</tex>, но проблема в том, что у <tex>X</tex> и <tex>Y</tex> уже есть вторая версия, добавлять | + | Пусть мы хотим добавить еще один элемент между узлами <tex>X</tex> и <tex>Y</tex>, но проблема в том, что у <tex>X</tex> и <tex>Y</tex> уже есть вторая версия, если будем добавлять еще новые версии, то получим дополнительный логарифм времени при обращении к узлу, как в рассмотренном выше методе "толстых" узлов. Поэтому более двух версий добавлять не будем. Используем метод копирования пути. Скопируем узлы <tex>X</tex> и <tex>Y</tex>, начиная с их третьей версии, и свяжем новые узлы с исходным списком. Для этого добавим вторые версии предыдущему перед <tex>X</tex> и последующему после <tex>Y</tex> узлам и свяжем эти узлы соответствующими ссылками. Так все версии остаются доступными. |
| − | [[Файл:Список2.png]] | + | [[Файл:Список2.png|700px]] |
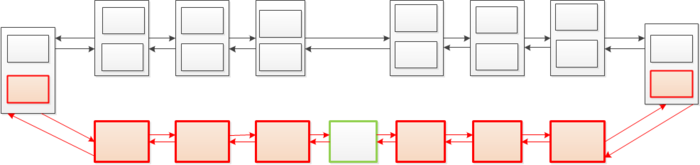
| − | Будем называть узел полным, если у него есть вторая версия. Если мы хотим вставить новый элемент в середину списка, мы должны склонировать все полные узлы слева и справа от места добавления нового узла, дойти до ближайших элементов, у которых нет второй версии и добавить им вторую версию. | + | Будем называть узел полным, если у него есть вторая версия. Если мы хотим вставить новый элемент в середину списка (на рисунке ниже он обозначен зеленым цветом), мы должны склонировать все полные узлы слева и справа от места добавления нового узла, дойти до ближайших элементов, у которых нет второй версии и добавить им вторую версию. |
| − | Оценим амортизационное время работы такого алгоритма. У нас частично персистентная структура данных, | + | [[Файл:Аморанализ.png|700px]] |
| + | |||
| + | Оценим амортизационное время работы такого алгоритма. У нас частично персистентная структура данных, изменять можно только ее последнюю версию. Примем функцию потенциала <tex>\Phi</tex> равной числу полных узлов в последней версии. | ||
| + | # Амортизационная стоимость операции добавления: | ||
| + | #* <tex>a_{empty} = t + \Delta\Phi = O(1) + 2 = O(1), </tex> так как если добавление узла не задевает полных узлов, то узел добавляется за константное время, а количество полных узлов увеличивается на <tex> 2 </tex>. | ||
| + | #* <tex>a_{fat} = t + \Delta\Phi = O(1) + k - k + 2 = O(1), </tex> так как если узел влечёт изменения полных узлов, то сначала потратится <tex> k </tex> времени на копирование этих полных узлов, и в то же время потенциал уменьшится на <tex> k </tex>, а потом увеличится максимум на <tex> 2 </tex>. | ||
| + | # Для любого <tex>i: \Phi_i = O(n),</tex> так как полных узлов не больше общего количества узлов в списке. | ||
| + | |||
| + | Таким образом, [[Амортизационный анализ#Метод потенциалов|по теореме о методе потенциалов]], амортизационное время работы по добавлению элемента будет <tex>O(1)</tex>. | ||
==Общий метод построения частично персистентных структур данных== | ==Общий метод построения частично персистентных структур данных== | ||
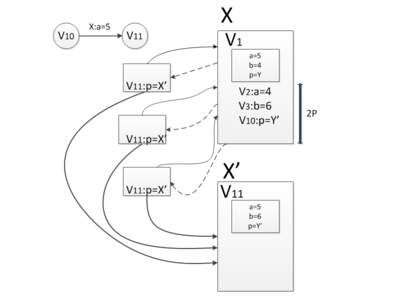
| − | + | [[Файл:Частичная персистентность.png|мини|справа|500x300px| Пунктирные линии — обратные ссылки,<br> <tex>X</tex> — исходный узел, актуальный до версии <tex>10</tex>,<br> | |
| − | + | <tex>X'</tex> — склонированный узел, актуальный с версии <tex>11</tex>, с пустым списком изменений]] | |
| − | + | Применим методы, описанные выше, в общем случае для абстрактной структуры данных. | |
| − | + | Пусть есть структура данных, у каждого узла которой количество указателей на этот узел не больше некоторой константы <tex>P</tex>. При клонировании узла важно знать, откуда на этот узел идут указатели, чтобы затем их переставить. Поэтому необходимо в каждом узле хранить обратные ссылки на те узлы, которые ссылаются на клонируемый узел. | |
| + | Все узлы будут храниться в виде «толстых» узлов, в которых содержится начальная версия этого узла и список внесенных в него изменений (англ. ''change log'') длиной не больше <tex>2P</tex>. | ||
| + | |||
| + | Пусть нужно внести изменение в структуру данных в узел <tex>X</tex>. Если есть место в списке изменений, просто вносим туда изменение: записываем номер версии, с которой начинается это изменение, в какое поле узла вносится изменение и какое именно. Если ''change log'' заполнен, то клонируем узел <tex>X</tex>: берем стартовую версию узла, производим в ней все изменения, записанные в ''change log'', добавляем последнее изменение и делаем версию со свободным списком изменений. Затем пройдем по обратным ссылкам от <tex>X</tex> и в ''change log'' каждого узла, ссылающегося на <tex>X</tex>, добавим изменение указателя начиная с этой версии структуры данных с <tex>X</tex> на <tex>X'</tex>. | ||
Оценим время работы этого алгоритма. Введем функцию потенциала, которая будет равна суммарному размеру всех списков изменений в последней версии. Посмотрим, как меняется суммарный размер списков изменений, когда мы совершаем одно изменение. Если ''change log'' был не полный, то мы просто добавляем туда один элемент, потенциал увеличится на единицу. | Оценим время работы этого алгоритма. Введем функцию потенциала, которая будет равна суммарному размеру всех списков изменений в последней версии. Посмотрим, как меняется суммарный размер списков изменений, когда мы совершаем одно изменение. Если ''change log'' был не полный, то мы просто добавляем туда один элемент, потенциал увеличится на единицу. | ||
| Строка 71: | Строка 107: | ||
==Получение полностью персистентных структур данных== | ==Получение полностью персистентных структур данных== | ||
Для полностью персистентных структур данных применить описанный выше метод преобразования не получится, так как история создания версий не линейна и нельзя отсортировать изменения по версиям, как в частично персистентных структурах данных. | Для полностью персистентных структур данных применить описанный выше метод преобразования не получится, так как история создания версий не линейна и нельзя отсортировать изменения по версиям, как в частично персистентных структурах данных. | ||
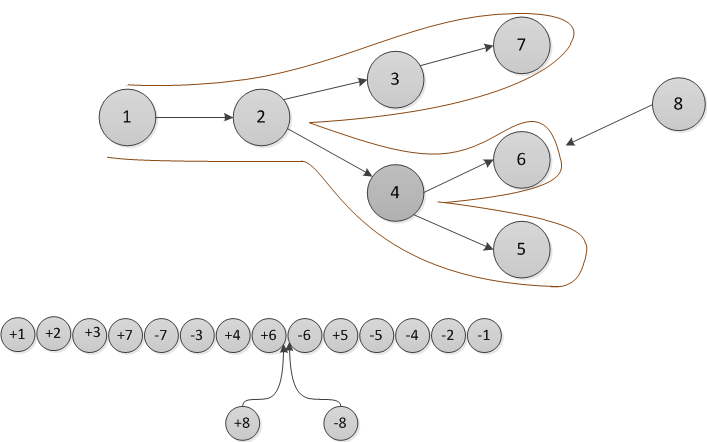
| − | Пусть мы храним историю изменения версий в виде дерева. Сделаем обход этого дерева в глубину. В порядке этого обхода запишем, когда мы входим, а когда выходим из каждой версии. Эта последовательность действий полностью задает дерево, сделаем из нее список. Когда добавляется новая версия | + | Пусть мы храним историю изменения версий в виде дерева. Сделаем[[Обход в глубину, цвета вершин| обход этого дерева в глубину]]. В порядке этого обхода запишем, когда мы входим, а когда выходим из каждой версии. Эта последовательность действий полностью задает дерево, сделаем из нее список. Когда после какой-то версии (на рисунке ниже это версия <tex>6</tex>) добавляется новая версия структуры данных (на рисунке версия <tex>8</tex>), мы вставляем два элемента в список (на рисунке это <tex>+8</tex> и <tex>-8</tex>) после входа, но до выхода из той версии, когда произошло изменение (то есть между |
| + | элементами <tex>+6</tex> и <tex>-6</tex>). Первый элемент вносит изменение, а второй будет возвращать обратно значение предыдущей версии. Таким образом, каждая операция разбивается на две: первая делает изменение, а вторая его откатывает. | ||
[[Файл:Полная персистентность.png]] | [[Файл:Полная персистентность.png]] | ||
| − | Для реализации описанного в предыдущем пункте метода преобразования структур данных в полностью персистентные нам нужен такой список, который поддерживает операции | + | Для реализации описанного в предыдущем пункте метода преобразования структур данных в полностью персистентные нам нужен такой список, который поддерживает операции <tex>\mathrm{insert After(p,q})</tex> (вставить <tex>q</tex> после <tex>p</tex>) и <tex>\mathrm{order(p,q)}</tex> (должен уметь отвечать на запросы вида "<tex>p</tex> лежит в этом списке до <tex>q</tex>"). <tex>\mathrm{order(p,q)}</tex> возвращает <tex>1</tex>, если <tex>p</tex> лежит до <tex>q</tex> и <tex>0</tex> иначе. Это список с поддержкой запроса о порядке [[List order maintenance|''List Order Maintenance'']], который обе эти операции делает за <tex>O(1)</tex>. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | В ''change log'' «толстого» узла теперь будем добавлять два события: одно указывает на изменение, произошедшее в соответствующей версии, а другое на его отмену. События будут добавляться в ''change log'' не по номерам версий, а по их порядку в списке версий ''List Order Maintenance''. | |
| − | + | Когда есть запрос к какой-то версии, то нужно найти в списке версий такую, после входа в которую, но до выхода из которой лежит версия запроса, а среди таких максимальную. Например, если приходит запрос к версии <tex>6</tex> на рисунке выше, то мы видим, что она в списке версий лежит после входа, но до выхода в версии <tex>1</tex>, <tex>2</tex> и <tex>4</tex>. Необходимо найти наибольшую из них. Список ''List Order Maintenance'' позволяет делать это за <tex>O(1)</tex> с помощью операции <tex>\mathrm{order(p,q)}</tex>. В примере это версия <tex>4</tex>. Так как ''change log'' каждого узла имеет константный размер, то поиск нужной версии в нем происходит за <tex>O(1)</tex>. | |
| + | В какой-то момент ''change log'' «толстого» узла переполнится. Тогда нужно клонировать этот узел и нижнюю половину изменений перенести в ''change log'' склонированного узла. Первую половину изменений применяем к исходной версии узла и сохраняем в качестве исходной в склонированном узле. | ||
| − | + | [[Файл:Полностью персистентные сд.png|900x700px]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | [[Файл: | ||
| − | + | Получится два узла: первый отвечает за отрезок версий до операции последнего изменения, а второй {{---}} после нее. Дальнейший порядок действий аналогичен тому, который использовался в общем методе построения частично персистентных структур данных. | |
| − | + | Оценим амортизационное время работы этого алгоритма. Введем функцию потенциала, равную числу полных узлов. Когда узел раздваивается, функция потенциала уменьшается на единицу, затем мы переставляем <tex>P</tex> ссылок, потенциал увеличивается на <tex>P</tex>, значит, амортизационное время работы — <tex>O(1)</tex>. | |
| − | |||
| − | |||
| − | + | ==Использование персистентных структур данных для решения геометрических задач== | |
| − | + | Персистентные структуры данных используются при решении геометрических задач. Примером может служить [[Локализация в ППЛГ методом полос (персистентные деревья)|Point location problem]] — задача о местоположении точки. Задачи такого рода решаются в ''offline'' и ''online''. В ''offline''-задачах все запросы даны заранее и можно обрабатывать их одновременно. В ''online''-задачах следующий запрос можно узнать только после того, как найден ответ на предыдущий. | |
| − | + | При решении ''offline''-задачи данный планарный граф разбивается на полосы вертикальными прямыми, проходящими через вершины многоугольников. Затем в этих полосах при помощи техники заметающей прямой ''(sweep line)'' ищется местоположение точки-запроса. При переходе из одной полосы в другую изменяется [[Дерево поиска, наивная реализация|сбалансированное дерево поиска]]. Если использовать частично персистентную структуру данных, то для каждой полосы будет своя версия дерева и сохранится возможность делать к ней запросы. Тогда ''Point location problem'' может быть решена в ''online''. | |
== См. также == | == См. также == | ||
| Строка 119: | Строка 136: | ||
* [[Персистентная очередь]] | * [[Персистентная очередь]] | ||
* [[Персистентный дек]] | * [[Персистентный дек]] | ||
| − | + | * [[List order maintance]] | |
| − | |||
| − | |||
| − | |||
== Источники информации == | == Источники информации == | ||
*[https://www.lektorium.tv/lecture/14321/ Дополнительные главы алгоритмов. Лекции Андрея Станкевича] | *[https://www.lektorium.tv/lecture/14321/ Дополнительные главы алгоритмов. Лекции Андрея Станкевича] | ||
*[http://logic.pdmi.ras.ru/csclub/node/2734/ Персистентные структуры данных. Лекции Павла Маврина] | *[http://logic.pdmi.ras.ru/csclub/node/2734/ Персистентные структуры данных. Лекции Павла Маврина] | ||
| + | |||
| + | |||
| + | [[Категория: Дискретная математика и алгоритмы]] | ||
| + | [[Категория: Персистентные структуры данных]] | ||
Текущая версия на 19:42, 4 сентября 2022
| Определение: |
| Персистентные структуры данных (англ. persistent data structure) — это структуры данных, которые при внесении в них каких-то изменений сохраняют все свои предыдущие состояния и доступ к этим состояниям. |
Уровни персистентности
Есть несколько уровней персистентности:
- частичная (англ. partial),
- полная (англ. full),
- конфлюэнтная (англ. confluent),
- функциональная (англ. functional).
В частично персистентных структурах данных к каждой версии можно делать запросы, но изменять можно только последнюю версию структуры данных.
В полностью персистентных структурах данных можно менять не только последнюю, но и любую версию структур данных, также к любой версии можно делать запросы.
Конфлюэнтные структуры данных позволяют объединять две структуры данных в одну (деревья поиска, которые можно сливать).
Функциональные структуры данных полностью персистентны по определению, так как в них запрещаются уничтожающие присваивания, т.е. любой переменной значение может быть присвоено только один раз и изменять значения переменных нельзя. Если структура данных функциональна, то она и конфлюэнтна, если конфлюэнтна, то и полностью персистентна, если полностью персистентна, то и частично персистентна. Однако бывают структуры данных не функциональные, но конфлюэнтные.
Способы преобразования структур данных в персистентные
Есть несколько способов сделать любую структуру персистентной:
- полное копирование (англ. full copy) когда при любой операции изменения полностью копируется структура данных и в получившуюся новую копию вносятся изменения,
- копирование пути (англ. path copying),
- метод «толстых» узлов (англ. fat node).
Рассмотрим для начала частичную персистентность. Для наглядности занумеруем разные версии структур данных. История изменений структуры данных линейна, в любой момент времени можно обратиться к любой версии структуры данных, но поменять возможно только последнюю версию (на рисунке она выделена синим цветом).
Сформулируем, что такое структура данных. В нашем понимании структурой данных будет называться набор узлов, в которых хранятся какие-то данные, и эти узлы связаны ссылками. Пример структуры данных — дерево. Рассмотрим, как методом копирования пути превратить дерево в персистентное.
Метод копирование пути
Пусть есть сбалансированное дерево поиска. Все операции в нем делаются за , где — высота дерева, а высота дерева , где — количество вершин. Пусть необходимо сделать какое-то обновление в этом сбалансированном дереве, например, добавить очередной элемент, но при этом нужно не потерять старое дерево. Возьмем узел, в который нужно добавить нового ребенка. Вместо того чтобы добавлять нового ребенка, скопируем этот узел, к копии добавим нового ребенка, также скопируем все узлы вплоть до корня, из которых достижим первый скопированный узел вместе со всеми указателями. Все вершины, из которых измененный узел не достижим, мы не трогаем. Количество новых узлов всегда будет порядка логарифма. В результате имеем доступ к обеим версиям дерева.
Так как рассматривается сбалансированное дерево поиска, то поднимая вершину вверх при балансировке, нужно делать копии всех вершин, участвующих во вращениях, у которых изменились ссылки на детей. Таких всегда не более трех, поэтому ассимптотика не пострадает. Когда балансировка закончится, нужно дойти вверх до корня, делая копии вершин на пути.
Этот метод хорошо работает на стеке, двоичных (декартовых, красно-черных) деревьях. Но в случае преобразования очереди в персистентную операция добавления будет очень дорогой, так как элемент добавляется в хвост очереди, который достижим из всех остальных элементов. Также не выгодно применять этот метод и в случае, когда в структуре данных имеются ссылки на родителя.
Реализация на основе дерева отрезков
На основе дерева отрезков можно построить полностью персистентную структуру данных.
Для реализации персистентного дерева отрезков удобно несколько изменить структуру дерева. Для этого будем использовать явные указатели и для дочерних элементов. Кроме того, заведем массив , в котором указывает на корень дерева отрезков версии
Для построения персистентного дерева отрезков из элементов необходимо применить раз операцию добавления элемента к последней версии дерева. Для того, чтобы добавить новый элемент к -ой версии дерева, необходимо проверить, является ли оно полным бинарным. Если да, то создадим новый корень, левым сыном сделаем . Иначе, сделаем копию корня исходной версии. Добавим корень в конец массива корней. Далее, спускаясь от корня к первому свободному листу, будем создавать несуществующие узлы и клонировать существующие. После этого в новой ветке необходимо обновить значение функции и некоторые указатели дочерних элементов. Поэтому, возвращаясь из рекурсии, будем менять один указатель на только что созданную или скопированную вершину, а также обновим значение функции, для которой строилось дерево. После этой операции в дереве появится новая версия, содержащая вставленный элемент.
Для того, чтобы изменить элемент в персистентном дереве отрезков, необходимо сделать следующие действия: спустимся в дереве от корня нужной версии до требуемого элемента, скопируем его, изменим значение, и, поднимаясь по дереву, будем клонировать узлы. При этом необходимо менять указатель на одного из детей на узел, созданный при предыдущем клонировании. После копирования корня, добавим новый корень в конец массива корней.
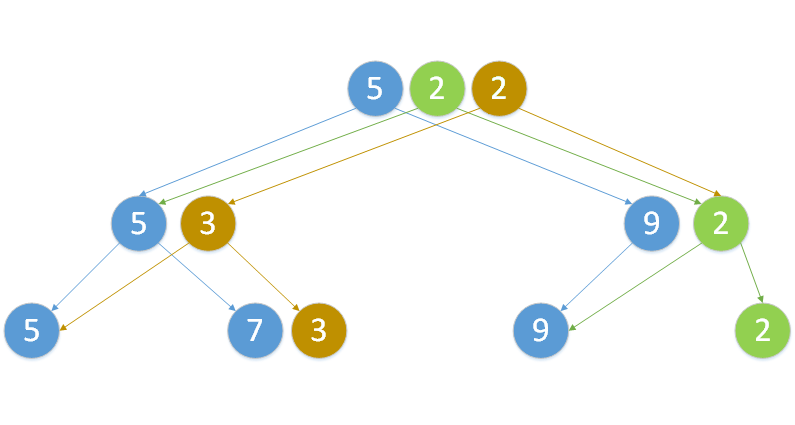
Здесь изображено персистентное дерево отрезков с операцией минимум, в котором изначально было 3 вершины. Сперва к нему была добавлена вершина со значением 2, а потом изменена вершина со значением 7. Цвет ребер и вершин соответствует времени их появления. Синий цвет элементов означает, что они были изначально, зеленый - что они появились после добавления, а оранжевый - что они появились после изменения элемента.
Метод «толстых» узлов
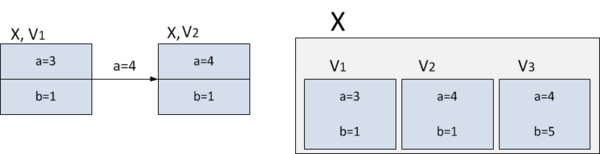
Пусть в структуре данных есть узел, в котором нужно сделать изменения (например, на рисунке ниже в первой версии структуры данных в узле есть поле , а во второй версии это поле должно быть равно ), но при этом нужно сохранить доступ к старой версии узла и не нужно экономить время. В таком случае можно хранить обе версии узла в большом комбинированном узле.
В примере выше в этом «толстом» узле будет храниться первая версия , у которой и вторая версия , у которой . Если далее последуют еще какие-то изменения (например, поле узла станет равно ) добавим в толстый узел еще одну версию — .
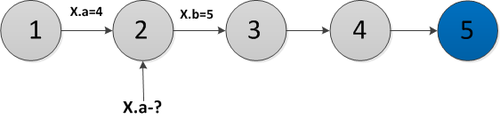
Пусть нужно сделать запрос ко второй версии структуры данных (на рисунке выше это запрос . Чтобы сделать этот запрос, нужно зайти в узел и найти в списке версий максимальную версию, которая меньше или равна версии запроса (в примере на рисунке это версия ), и в этой версии узла найти значение поля (в примере ). Чтобы быстро найти нужную версию в списке версий, хранящихся в «толстом» узле, нужно хранить их в виде дерева. Тогда мы сможем за логарифм найти нужную версию и к ней обратиться. Значит, все операции, которые будут производиться на этой структуре данных, будут домножаться на логарифм от числа версий.
Структура толстого узла может быть и другой: к каждой вершине можно хранить лог ее изменений, в который записывается версия, в которой произошло изменение, а также само изменение. Такая структура толстого узла рассмотрена ниже, в разделах об общих методах получения частично и полностью персистентных структур данных. Лог может быть организован по-разному. Обычно делают отдельный лог для каждого поля вершины. Когда что-то меняется в вершине, то в лог соответствующего поля записывается это изменение и номер версии, с которой данное изменение произошло. Когда нужно обратиться к старой версии, то двоичным поиском ищут в логе последнее изменение до этой версии и находят нужное значение. Метод fat node дает замедление , где — число изменений структуры данных; памяти требуется , где — число вершин в структуре данных.
Преобразование списка в персистентный за O(1)
Если скомбинировать методы path copiyng и fat node, то получим универсальный метод, который позволит преобразовывать структуры данных в частично персистентные без дополнительного логарифма памяти и времени. Пусть мы имеем двусвязный список и хотим внести в него какое-то изменение, например, добавить узел между узлами и , то есть при переходе из версии в версию добавим в двусвязный список узел . Применим метод «толстых» узлов. Для этого в узлы и добавим вторую версию и изменим ссылку, следующую из , и предыдущую перед , как показано на рисунке. Этот алгоритм работает следующим образом. Например, текущая первая версия. Идем по списку слева направо от первого узла к узлу , а затем нужно перейти к следующему узлу. В «толстом» узле выбираем нужную (первую) версию и далее следуем по ссылкам.
Пусть мы хотим добавить еще один элемент между узлами и , но проблема в том, что у и уже есть вторая версия, если будем добавлять еще новые версии, то получим дополнительный логарифм времени при обращении к узлу, как в рассмотренном выше методе "толстых" узлов. Поэтому более двух версий добавлять не будем. Используем метод копирования пути. Скопируем узлы и , начиная с их третьей версии, и свяжем новые узлы с исходным списком. Для этого добавим вторые версии предыдущему перед и последующему после узлам и свяжем эти узлы соответствующими ссылками. Так все версии остаются доступными.
Будем называть узел полным, если у него есть вторая версия. Если мы хотим вставить новый элемент в середину списка (на рисунке ниже он обозначен зеленым цветом), мы должны склонировать все полные узлы слева и справа от места добавления нового узла, дойти до ближайших элементов, у которых нет второй версии и добавить им вторую версию.
Оценим амортизационное время работы такого алгоритма. У нас частично персистентная структура данных, изменять можно только ее последнюю версию. Примем функцию потенциала равной числу полных узлов в последней версии.
- Амортизационная стоимость операции добавления:
- так как если добавление узла не задевает полных узлов, то узел добавляется за константное время, а количество полных узлов увеличивается на .
- так как если узел влечёт изменения полных узлов, то сначала потратится времени на копирование этих полных узлов, и в то же время потенциал уменьшится на , а потом увеличится максимум на .
- Для любого так как полных узлов не больше общего количества узлов в списке.
Таким образом, по теореме о методе потенциалов, амортизационное время работы по добавлению элемента будет .
Общий метод построения частично персистентных структур данных
Применим методы, описанные выше, в общем случае для абстрактной структуры данных.
Пусть есть структура данных, у каждого узла которой количество указателей на этот узел не больше некоторой константы . При клонировании узла важно знать, откуда на этот узел идут указатели, чтобы затем их переставить. Поэтому необходимо в каждом узле хранить обратные ссылки на те узлы, которые ссылаются на клонируемый узел. Все узлы будут храниться в виде «толстых» узлов, в которых содержится начальная версия этого узла и список внесенных в него изменений (англ. change log) длиной не больше .
Пусть нужно внести изменение в структуру данных в узел . Если есть место в списке изменений, просто вносим туда изменение: записываем номер версии, с которой начинается это изменение, в какое поле узла вносится изменение и какое именно. Если change log заполнен, то клонируем узел : берем стартовую версию узла, производим в ней все изменения, записанные в change log, добавляем последнее изменение и делаем версию со свободным списком изменений. Затем пройдем по обратным ссылкам от и в change log каждого узла, ссылающегося на , добавим изменение указателя начиная с этой версии структуры данных с на .
Оценим время работы этого алгоритма. Введем функцию потенциала, которая будет равна суммарному размеру всех списков изменений в последней версии. Посмотрим, как меняется суммарный размер списков изменений, когда мы совершаем одно изменение. Если change log был не полный, то мы просто добавляем туда один элемент, потенциал увеличится на единицу. Если change log был полный, то потенциал уменьшается на его размер, так как мы склонировали узел с пустым списком изменений. После этого мы пошли по обратным ссылкам (их было штук) и добавили в узлов по одному значению. Таким образом амортизированное время работы будет .
Получение полностью персистентных структур данных
Для полностью персистентных структур данных применить описанный выше метод преобразования не получится, так как история создания версий не линейна и нельзя отсортировать изменения по версиям, как в частично персистентных структурах данных. Пусть мы храним историю изменения версий в виде дерева. Сделаем обход этого дерева в глубину. В порядке этого обхода запишем, когда мы входим, а когда выходим из каждой версии. Эта последовательность действий полностью задает дерево, сделаем из нее список. Когда после какой-то версии (на рисунке ниже это версия ) добавляется новая версия структуры данных (на рисунке версия ), мы вставляем два элемента в список (на рисунке это и ) после входа, но до выхода из той версии, когда произошло изменение (то есть между элементами и ). Первый элемент вносит изменение, а второй будет возвращать обратно значение предыдущей версии. Таким образом, каждая операция разбивается на две: первая делает изменение, а вторая его откатывает.
Для реализации описанного в предыдущем пункте метода преобразования структур данных в полностью персистентные нам нужен такой список, который поддерживает операции (вставить после ) и (должен уметь отвечать на запросы вида " лежит в этом списке до "). возвращает , если лежит до и иначе. Это список с поддержкой запроса о порядке List Order Maintenance, который обе эти операции делает за .
В change log «толстого» узла теперь будем добавлять два события: одно указывает на изменение, произошедшее в соответствующей версии, а другое на его отмену. События будут добавляться в change log не по номерам версий, а по их порядку в списке версий List Order Maintenance.
Когда есть запрос к какой-то версии, то нужно найти в списке версий такую, после входа в которую, но до выхода из которой лежит версия запроса, а среди таких максимальную. Например, если приходит запрос к версии на рисунке выше, то мы видим, что она в списке версий лежит после входа, но до выхода в версии , и . Необходимо найти наибольшую из них. Список List Order Maintenance позволяет делать это за с помощью операции . В примере это версия . Так как change log каждого узла имеет константный размер, то поиск нужной версии в нем происходит за .
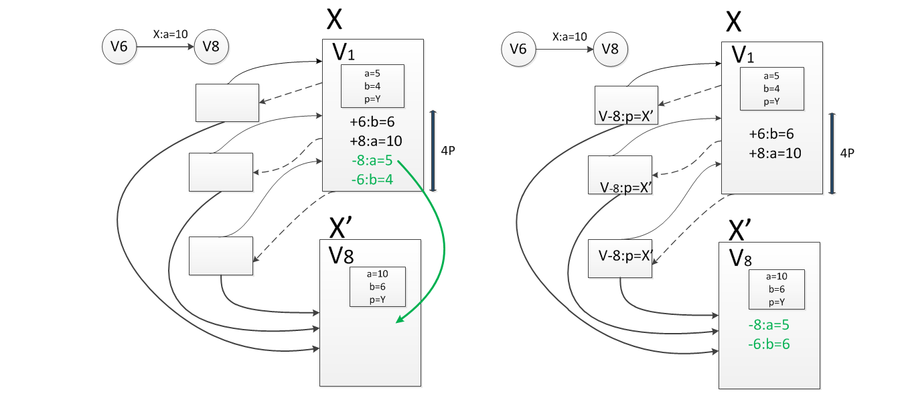
В какой-то момент change log «толстого» узла переполнится. Тогда нужно клонировать этот узел и нижнюю половину изменений перенести в change log склонированного узла. Первую половину изменений применяем к исходной версии узла и сохраняем в качестве исходной в склонированном узле.
Получится два узла: первый отвечает за отрезок версий до операции последнего изменения, а второй — после нее. Дальнейший порядок действий аналогичен тому, который использовался в общем методе построения частично персистентных структур данных.
Оценим амортизационное время работы этого алгоритма. Введем функцию потенциала, равную числу полных узлов. Когда узел раздваивается, функция потенциала уменьшается на единицу, затем мы переставляем ссылок, потенциал увеличивается на , значит, амортизационное время работы — .
Использование персистентных структур данных для решения геометрических задач
Персистентные структуры данных используются при решении геометрических задач. Примером может служить Point location problem — задача о местоположении точки. Задачи такого рода решаются в offline и online. В offline-задачах все запросы даны заранее и можно обрабатывать их одновременно. В online-задачах следующий запрос можно узнать только после того, как найден ответ на предыдущий.
При решении offline-задачи данный планарный граф разбивается на полосы вертикальными прямыми, проходящими через вершины многоугольников. Затем в этих полосах при помощи техники заметающей прямой (sweep line) ищется местоположение точки-запроса. При переходе из одной полосы в другую изменяется сбалансированное дерево поиска. Если использовать частично персистентную структуру данных, то для каждой полосы будет своя версия дерева и сохранится возможность делать к ней запросы. Тогда Point location problem может быть решена в online.