Список
Связный список (англ. List) — структура данных, состоящая из элементов, содержащих помимо собственных данных ссылки на следующий и/или предыдущий элемент списка. С помощью списков можно реализовать такие структуры данных как стек и очередь.
Односвязный список
Двусвязный список
Также хранится указатель на предыдущий элемент списка, благодаря чему становится проще удалять и переставлять элементы.
XOR-связный список
В некоторых случаях использование двусвязного списка в явном виде является нецелесообразным. В целях экономии памяти можно хранить только результат выполнения операции Xor над адресами предыдущего и следующего элементов списка. Таким образом, зная адрес предыдущего элемента, мы можем вычислить адрес следующего элемента.
Циклический список
Операции на списке
Рассмотрим базовые операции на примере односвязного списка.
Вставка
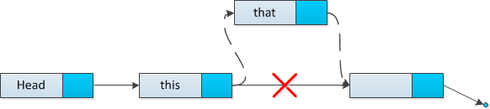
Очевиден случай, когда необходимо добавить элемент () в голову списка. Установим в этом элементе ссылку на старую голову, и обновим указатель на голову.
function insert(Node thatElement): thatElement.next = thisElement.next thisElement.next = thatElement
Поиск
Для того, чтобы найти элемент по значению (), будем двигаться по списку от головы до конца и сравнивать значение в элементах с искомым. Если элемента в списке нет, то возвращаем .
Node search(int value):
node = head
while node != NULL and value != node.value
node = node.next
return node
Удаление
Для того, чтобы удалить голову списка, переназначим указатель на голову на второй элемент списка, а голову удалим.
function removeHead():
if head != NULL
tmp = head
head = head.next
delete tmp
Удаление элемента после заданного () происходит следующим образом: изменим ссылку на следующий элемент на следующий за удаляемым, затем удалим нужный объект.
function removeAfter(Node thisElement):
if thisElement.next != NULL
tmp = thisElement.next
thisElement.next = thisElement.next.next
delete tmp
Поиск цикла в списке
Для начала необходимо уметь определять — список циклический или нет. Воспользуемся алгоритмом Флойда "Черепаха и заяц". Пусть за одну итерацию первый указатель (черепаха) переходит к следующему элементу списка, а второй указатель (заяц) на два элемента вперед. Тогда, если эти два указателя встретятся, то цикл найден, если дошли до конца списка, то цикла нет.
boolean hasCycle(Node head):
tortoise = head
hare = head
repeat
if hare == NULL or hare.next == NULL
return false
tortoise = tortoise.next
hare = hare.next.next
until tortoise == hare
return true
Если цикла не существует, то заяц первым дойдет до конца и функция возвратит . В другом случае, в тот момент, когда и черепаха и заяц находятся в цикле, расстояние между ними будет сокращаться на , что гарантирует их встречу за конечное время.
Поиск длины хвоста в списке с циклом
Так как для поиска хвоста мы должны знать, что цикл существует, воспользуемся предыдущей функцией и при выходе из неё запомним "момент встречи" зайца и черепахи. Назовем её .
Наивные реализации
Реализация за
Будем последовательно идти от начала цикла и проверять, лежит ли этот элемент на цикле. На каждой итерации запустим от вперёд указатель. Если он окажется в текущем элементе, прежде чем посетит снова, то точку окончания (начала) хвоста нашли.
Реализация за
Реализацию, приведенную выше можно улучшить. Для этого воспользуемся бинарным поиском. Сначала проверим голову списка, потом сделаем шага вперёд, потом , потом и так далее, пока не окажемся на цикле. Теперь у нас есть две позиции — на левой границе, где мы в хвосте, и на правой — в цикле. Сделаем бинарный поиск уже по этому отрезку и таким образом найдём цикл за .
Эффективная реализация
Возможны два варианта цикла в списке. Первый вариант — сам список циклический (указатель последнего элемента равен первому), а второй вариант — цикл внутри списка (указатель последнего элемента равен любому другому (не первому)). В первом случае найти длину цикла тривиально, во второй случай сводится к первому, если найти указатель на начало цикла. Достаточно запустить один указатель из , а другой из головы с одной скоростью. Элемент, где оба указателя встретятся, будет началом цикла. Сложность алгоритма — . Ниже приведена функция, которая находит эту точку, а возвращает длину хвоста списка.
int getTail(Node head, Node pointMeeting):
firstElement = head.next
secondElement = pointMeeting.next
lengthTail = 1
while firstElement != secondElement
firstElement = firstElement.next
secondElement = secondElement.next
lengthTail = lenghtTail + 1
return lengthTail
Доказательство корректности алгоритма
Рассмотрим цикл длиной с хвостом длины . Напишем функции для обоих указателей в зависимости от шага . Очевидно, что встреча не может произойти при , так как в этом случае для любого . Тогда положения указателей зададутся следующими функциями (при ):
Приравнивая, получим , или . Пусть — голова списка, — точка встречи, — первый элемент цикла, — расстояние от до . Тогда в точку можно прийти двумя путями: из в длиной и из через в длиной , то есть:
, но так как
Пусть
Известно, что
откуда
Подставив полученные значения, получим: , откуда следует, что если запустить указатели с одной скоростью из и , то они встретятся через шагов в точке . К этому времени вышедший из пройдёт ровно шагов и остановится в , вышедший из накрутит по циклу шагов и пройдёт ещё шагов. Поскольку , то они встретятся как раз в точке .
Задача про обращение списка
Для того, чтобы обратить список, необходимо пройти по всем элементам этого списка, и все указатели на следующий элемент заменить на предыдущий. Эта рекурсивная функция принимает указатель на голову списка и предыдущий элемент (при запуске указывать ), а возвращает указатель на новую голову списка.
Node reverse(Node current, Node prev):
if current == NULL
return prev
next = current.next
current.next = prev
return reverse(next, current)
Алгоритм корректен, поскольку значения элементов в списке не изменяются, а все указатели изменят свое направление, не нарушив связности самого списка.
См.также
Источники информации
- Wikipedia — Linked list
- Википедия — Список
- Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ — 2-е изд. — М.: «Вильямс», 2007. — Глава 11.2. — ISBN 5-8489-0857-4
- Дональд Э. Кнут Искусство программирования. Том 1. Основные алгоритмы — 2-е изд. — М.: «Вильямс», 2012. — Глава 2.2. — ISBN 0-201-89685-0