Представление производящей функций в виде непрерывных дробей — различия между версиями
(→Разложение дробно-рациональной производящей функции) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 6 промежуточных версий 2 участников) | |||
| Строка 60: | Строка 60: | ||
Возведя ее в квадрат и умножив результат на <tex>s</tex>, получим | Возведя ее в квадрат и умножив результат на <tex>s</tex>, получим | ||
| − | <tex>sCat^2(s) = c^2_0s + (c_0c_1 + c_1c_0)s^2 + (c_0c_2 + c_1c_1 + c_2c_0)s^ | + | <tex>sCat^2(s) = c^2_0s + (c_0c_1 + c_1c_0)s^2 + (c_0c_2 + c_1c_1 + c_2c_0)s^3 + \cdots = s + 2s^2 + 5s^3 + 14s^4 + \cdots = Cat(s) − 1,</tex> |
что дает нам квадратное уравнение на производящую функцию | что дает нам квадратное уравнение на производящую функцию | ||
| Строка 72: | Строка 72: | ||
или | или | ||
| − | <tex>Cat(s) = \cfrac{1}{1 - sCat | + | <tex>Cat(s) = \cfrac{1}{1 - sCat(s)}.</tex> |
Подставив выражение для <tex>Cat(s)</tex> из левой части равенства в | Подставив выражение для <tex>Cat(s)</tex> из левой части равенства в | ||
| Строка 101: | Строка 101: | ||
Изменим несколько треугольник Дика, поставив на стрелках числа. А именно, поставим на каждой стрелке номер того ряда, в котором она находится. Номер на стрелке | Изменим несколько треугольник Дика, поставив на стрелках числа. А именно, поставим на каждой стрелке номер того ряда, в котором она находится. Номер на стрелке | ||
| − | мы будем интерпретировать как ее кратность, то есть как число различных стрелок, проходящих в данном направлении. В результате одному пути в треугольнике Дика отвечает несколько «различных» путей в треугольнике с кратностями. Их число равно произведению кратностей всех ребер, входящих в данный путь. То есть значение элемента треугольника | + | мы будем интерпретировать как ее кратность, то есть как число различных стрелок, проходящих в данном направлении. В результате одному пути в треугольнике Дика отвечает несколько «различных» путей в треугольнике с кратностями. Их число равно произведению кратностей всех ребер, входящих в данный путь. То есть значение элемента треугольника, которому раньше соответствовал путь в точку плоскости <tex>(m;n)</tex>, теперь равно следующему: <tex>c_{m,n} = (n+1)c_{m-1,n+1}+nc_{m-1,n-1}</tex>. |
[[Файл:R6.PNG]] | [[Файл:R6.PNG]] | ||
Текущая версия на 19:27, 4 сентября 2022
Содержание
Определения
| Определение: |
| Непрерывная дробь (англ. continued fraction) — это конечное или бесконечное математическое выражение вида
где и есть целые числа, а — натуральные числа (положительные целые). |
Если для всех , выражение называется простой непрерывной дробью (англ. regular continued fraction).
В некоторой литературе вместо термина «непрерывная дробь» используют термин «цепная дробь».
| Определение: |
| Конечная непрерывная дробь (англ. finite continued fraction) — это непрерывная дробь, которая состоит из конечных наборов и |
| Определение: |
| K-подходящей дробью (англ. k-suitable fraction) непрерывной дроби называют обыкновенную дробь , где , а - многочлены -ой степени |
Разложение дробно-рациональной производящей функции
| Утверждение: |
Дробно-рациональная производящая функция всегда раскладывается в конечную непрерывную дробь. |
|
Если у нас есть дробно-рациональная производящая функция
то в общем случае:
где
и
Аналогично
где
и
и так далее. Таким Образом При чем легко убедиться, что непрерывная дробь получится конечной. |
Функция Каталана в виде непрерывной дроби
Рассмотрим производящую функцию для чисел Каталана
Возведя ее в квадрат и умножив результат на , получим
что дает нам квадратное уравнение на производящую функцию
Перепишем это уравнение в виде
или
Подставив выражение для из левой части равенства в правую часть того же равенства, получим
Подставляя вновь выражение для в получившееся равенство и продолжая этот процесс, мы получаем представление для функции Каталана в виде непрерывной дроби:
Полученное разложение нужно понимать следующим образом. Если мы оборвем непрерывную дробь на -м шаге (оставив вместо нее конечную непрерывную дробь, которая представляет собой рациональную функцию), то коэффициенты разложения полученной функции по степеням будут совпадать с коэффициентами разложения функции вплоть до члена . Заметим, что из-за наличия множителя в числителе очередной дроби, присоединяемой на -м шаге, увеличение числа членов в непрерывной дроби не приводит к изменению первых коэффициентов в ее разложении. Например,
Стабилизирующаяся часть разложения выделена.
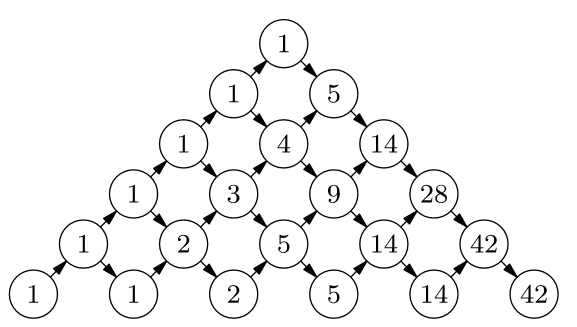
Треугольник Дика
Треугольник Дика перечисляет пути в положительном квадранте плоскости, выходящие из начала координат и составленные из векторов и .
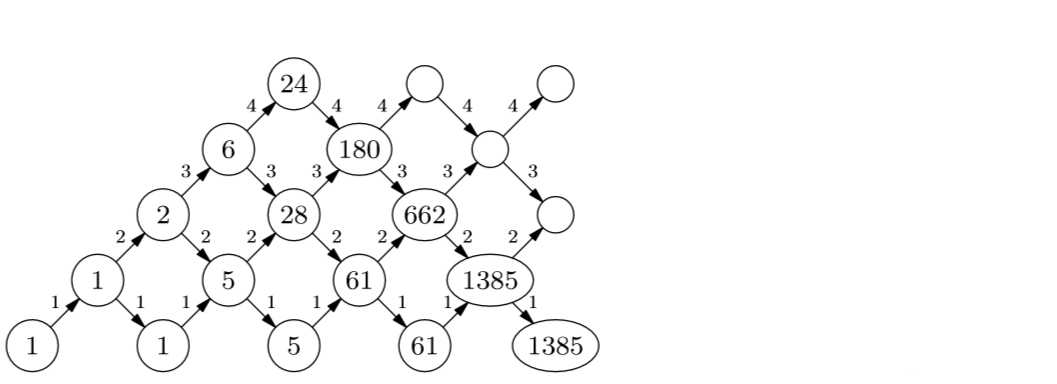
Изменим несколько треугольник Дика, поставив на стрелках числа. А именно, поставим на каждой стрелке номер того ряда, в котором она находится. Номер на стрелке мы будем интерпретировать как ее кратность, то есть как число различных стрелок, проходящих в данном направлении. В результате одному пути в треугольнике Дика отвечает несколько «различных» путей в треугольнике с кратностями. Их число равно произведению кратностей всех ребер, входящих в данный путь. То есть значение элемента треугольника, которому раньше соответствовал путь в точку плоскости , теперь равно следующему: .
| Теорема: |
Производящая функция для нижней стороны треугольника Дика представляется в
виде непрерывной дроби |
| Доказательство: |
|
Производящая функция перечисляет различные пути с началом и концом на высоте . Обозначим через производящую функцию, перечисляющую пути с началом и концом на высоте , которые не опускаются ниже уровня , по их длине. Тогда
Действительно, каждый путь с началом и концом на высоте единственным образом разбивается на такие участки, что
Если отбросить начальный и конечный отрезок такого участка, то мы получим путь, начинающийся и заканчивающийся на высоте . Аналогично,
Появление четверки в коэффициенте при объясняется тем, что к данному пути, начало и конец которого лежат на высоте , начальный и конечный векторы, превращающие его в путь на высоте , можно добавить четырьмя «различными» способами. Продолжая это рассуждение, мы заключаем, что
и непрерывная дробь теперь выписывается очевидным образом: |
См. также
Источники информации
- Лекции о производящих функциях
- Непрерывная дробь
- Демидович Б. П., Марон И. А. Основы вычислительной математики. — Изд. 2-е. — М.: Физматлит, 1963. — С. 53—73. — 660 с.