Представление производящей функций в виде непрерывных дробей
Содержание
Определения
| Определение: |
| Непрерывная дробь (англ. continued fraction) — это конечное или бесконечное математическое выражение вида
где и есть целые числа, а — натуральные числа (положительные целые). |
Если для всех , выражение называется простой непрерывной дробью (англ. regular continued fraction).
В некоторой литературе вместо термина «непрерывная дробь» используют термин «цепная дробь».
| Определение: |
| Конечная непрерывная дробь (англ. finite continued fraction) — это непрерывная дробь, которая состоит из конечных наборов и |
| Определение: |
| K-подходящей дробью (англ. k-suitable fraction) непрерывной дроби называют обыкновенную дробь , где , а - многочлены -ой степени |
Разложение дробно-рациональной производящей функции
| Утверждение: |
Дробно-рациональная производящая функция всегда раскладывается в конечную непрерывную дробь. |
|
Если у нас есть дробно-рациональная производящая функция
то в общем случае:
где
и
Аналогично
где
и
и так далее. Таким Образом При чем легко убедиться, что непрерывная дробь получится конечной. |
Функция Каталана в виде непрерывной дроби
Рассмотрим производящую функцию для чисел Каталана
Возведя ее в квадрат и умножив результат на , получим
что дает нам квадратное уравнение на производящую функцию
Перепишем это уравнение в виде
или
Подставив выражение для из левой части равенства в правую часть того же равенства, получим
Подставляя вновь выражение для в получившееся равенство и продолжая этот процесс, мы получаем представление для функции Каталана в виде непрерывной дроби:
Полученное разложение нужно понимать следующим образом. Если мы оборвем непрерывную дробь на -м шаге (оставив вместо нее конечную непрерывную дробь, которая представляет собой рациональную функцию), то коэффициенты разложения полученной функции по степеням будут совпадать с коэффициентами разложения функции вплоть до члена . Заметим, что из-за наличия множителя в числителе очередной дроби, присоединяемой на -м шаге, увеличение числа членов в непрерывной дроби не приводит к изменению первых коэффициентов в ее разложении. Например,
Стабилизирующаяся часть разложения выделена.
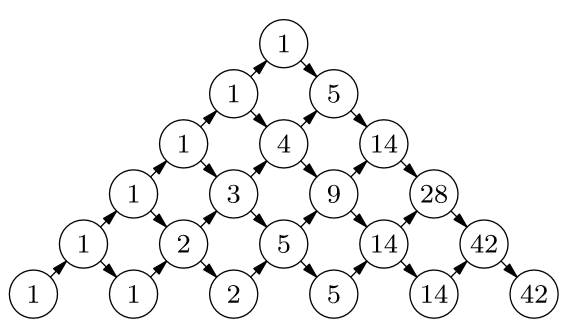
Треугольник Дика
Треугольник Дика перечисляет пути в положительном квадранте плоскости, выходящие из начала координат и составленные из векторов и .
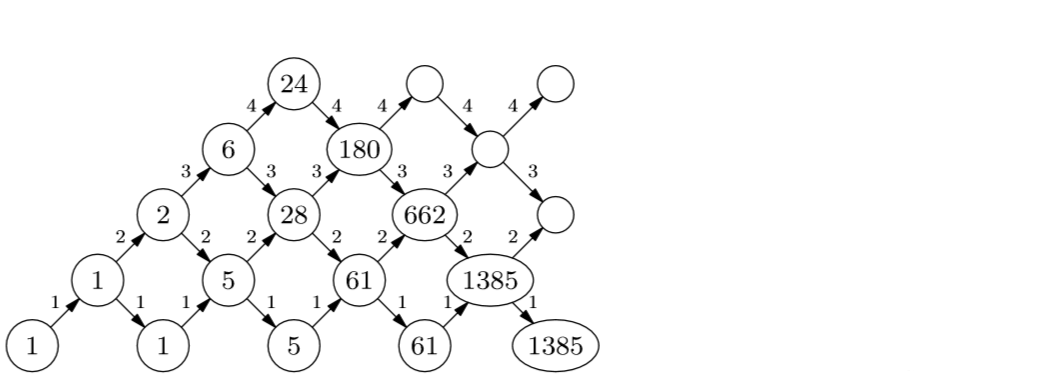
Изменим несколько треугольник Дика, поставив на стрелках числа. А именно, поставим на каждой стрелке номер того ряда, в котором она находится. Номер на стрелке мы будем интерпретировать как ее кратность, то есть как число различных стрелок, проходящих в данном направлении. В результате одному пути в треугольнике Дика отвечает несколько «различных» путей в треугольнике с кратностями. Их число равно произведению кратностей всех ребер, входящих в данный путь. То есть значение элемента треугольника, которому раньше соответствовал путь в точку плоскости , теперь равно следующему: .
| Теорема: |
Производящая функция для нижней стороны треугольника Дика представляется в
виде непрерывной дроби |
| Доказательство: |
|
Производящая функция перечисляет различные пути с началом и концом на высоте . Обозначим через производящую функцию, перечисляющую пути с началом и концом на высоте , которые не опускаются ниже уровня , по их длине. Тогда
Действительно, каждый путь с началом и концом на высоте единственным образом разбивается на такие участки, что
Если отбросить начальный и конечный отрезок такого участка, то мы получим путь, начинающийся и заканчивающийся на высоте . Аналогично,
Появление четверки в коэффициенте при объясняется тем, что к данному пути, начало и конец которого лежат на высоте , начальный и конечный векторы, превращающие его в путь на высоте , можно добавить четырьмя «различными» способами. Продолжая это рассуждение, мы заключаем, что
и непрерывная дробь теперь выписывается очевидным образом: |
См. также
Источники информации
- Лекции о производящих функциях
- Непрерывная дробь
- Демидович Б. П., Марон И. А. Основы вычислительной математики. — Изд. 2-е. — М.: Физматлит, 1963. — С. 53—73. — 660 с.