Доказательство нерегулярности языков: лемма о разрастании — различия между версиями
Zarubkin (обсуждение | вклад) |
Zarubkin (обсуждение | вклад) |
||
| Строка 5: | Строка 5: | ||
Пусть <tex>L</tex> - регулярный язык над алфавитом <tex>\Sigma</tex>, тогда существует <tex>n</tex>, такой что для любого слова <tex> \omega \in L</tex>, длины не меньше <tex> n </tex> найдутся слова <tex> x,y,z \in \Sigma^*</tex>, для которых верно <tex>xyz=\omega, y\neq \varepsilon, |xy|\leqslant n</tex> и <tex>xy^{k}z\in L</tex> для всех <tex> k \geqslant 0</tex>. | Пусть <tex>L</tex> - регулярный язык над алфавитом <tex>\Sigma</tex>, тогда существует <tex>n</tex>, такой что для любого слова <tex> \omega \in L</tex>, длины не меньше <tex> n </tex> найдутся слова <tex> x,y,z \in \Sigma^*</tex>, для которых верно <tex>xyz=\omega, y\neq \varepsilon, |xy|\leqslant n</tex> и <tex>xy^{k}z\in L</tex> для всех <tex> k \geqslant 0</tex>. | ||
|proof= | |proof= | ||
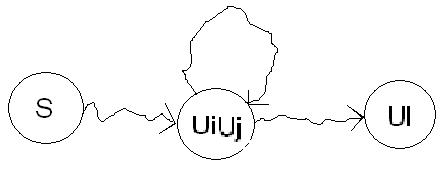
| − | Пусть <tex>L</tex> - регулярный язык над алфавитом <tex>\Sigma</tex>, тогда найдётся автомат <tex>A</tex>, допускающий язык <tex>L</tex>. Обозначим размер автомата <tex>A</tex>, как <tex>n</tex>. В языке <tex>L</tex> найдётся слово <tex>\omega</tex> длины не меньше <tex>n</tex>. Рассмотрим переходы в автомате <tex>\langle s,\omega\rangle \vdash\langle u_1, \omega[0]^{-1}\omega\rangle\vdash\dots\vdash\langle u_{l},\epsilon\rangle, \: l\geqslant n</tex>. Так как <tex>l</tex> не меньше количества состояний в автомате <tex>n</tex>, то в переходах будет совпадение. Пусть <tex>u_i</tex> и <tex>u_j</tex> - первое совпадение. Тогда в нашем слове <tex>\omega</tex> можно размножить кусок, который отвечает за переход, от состояния <tex>u_i</tex> к состоянию <tex>u_j</tex>. То есть если верно <tex>\langle s, xyz\rangle \vdash^*\langle u_i, yz\rangle\vdash^*\langle u_j, z\rangle\vdash^*\langle u_l, \varepsilon\rangle</tex>, то тогда верно <tex>\langle s, xy^kz\rangle \vdash^*\langle u_i, y^kz\rangle\vdash^*\langle u_j, y^{k-1}z\rangle\vdash^*\langle u_j, z\rangle\vdash^*\langle u_l, \varepsilon\rangle</tex>. Тогда автомат <tex>A</tex> допускает слово <tex>xy^kz</tex>, следовательно <tex>xy^kz</tex> принадлежит регулярному языку <tex>L</tex>. | + | Пусть <tex>L</tex> - регулярный язык над алфавитом <tex>\Sigma</tex>, тогда найдётся автомат <tex>A</tex>, допускающий язык <tex>L</tex>. Обозначим размер автомата <tex>A</tex>, как <tex>n</tex>. В языке <tex>L</tex> найдётся слово <tex>\omega</tex> длины не меньше <tex>n</tex>. Рассмотрим переходы в автомате <tex>\langle s,\omega\rangle \vdash\langle u_1, \omega[0]^{-1}\omega\rangle\vdash\dots\vdash\langle u_{l},\epsilon\rangle, \: l\geqslant n</tex>. Так как <tex>l</tex> не меньше количества состояний в автомате <tex>n</tex>, то в переходах будет совпадение. Пусть <tex>u_i</tex> и <tex>u_j</tex> - первое совпадение. Тогда в нашем слове <tex>\omega</tex> можно размножить кусок, который отвечает за переход, от состояния <tex>u_i</tex> к состоянию <tex>u_j</tex>. |
| + | |||
| + | [[Файл:Regularpumpingpicture.jpg]] | ||
| + | |||
| + | |||
| + | То есть если верно <tex>\langle s, xyz\rangle \vdash^*\langle u_i, yz\rangle\vdash^*\langle u_j, z\rangle\vdash^*\langle u_l, \varepsilon\rangle</tex>, то тогда верно <tex>\langle s, xy^kz\rangle \vdash^*\langle u_i, y^kz\rangle\vdash^*\langle u_j, y^{k-1}z\rangle\vdash^*\langle u_j, z\rangle\vdash^*\langle u_l, \varepsilon\rangle</tex>. Тогда автомат <tex>A</tex> допускает слово <tex>xy^kz</tex>, следовательно <tex>xy^kz</tex> принадлежит регулярному языку <tex>L</tex>. | ||
| − | |||
}} | }} | ||
Версия 23:02, 14 октября 2010
| Лемма (О разрастании): |
Пусть - регулярный язык над алфавитом , тогда существует , такой что для любого слова , длины не меньше найдутся слова , для которых верно и для всех . |
| Доказательство: |
|
Пусть - регулярный язык над алфавитом , тогда найдётся автомат , допускающий язык . Обозначим размер автомата , как . В языке найдётся слово длины не меньше . Рассмотрим переходы в автомате . Так как не меньше количества состояний в автомате , то в переходах будет совпадение. Пусть и - первое совпадение. Тогда в нашем слове можно размножить кусок, который отвечает за переход, от состояния к состоянию .
|
Доказательство нерегулярности языка
Чаще используется отрицание леммы для доказательства нерегулярности языка. Пусть - язык над алфавитом . Если для любого натурального найдётся такое слово из данного языка, что его длина будет не меньше и при любом разбиении на три слова такие, что не пустое слово, длина не больше , есть такое, что , то язык - не регулярный.
Пример 1 Язык правильных скобочных последовательностей не регулярен.
Пусть дан какой-то для него предъявляем слово . После этого слово как-то разбили на . Так как , то из-за выбранного слова , где больше нуля. Для любого такого разбиения берём и получаем , что не является правильной скобочной последовательностью. Значит язык правильных скобочных последовательностей не регулярный язык.
Пример 2 Язык
Пусть дан какой-то для него предъявляем слово . После этого слово как-то разбили на . Так как , то из-за выбранного слова , где больше нуля. Для любого такого разбиения берём и получаем , что не является элементом множества слов языка , значит этот язык не регулярен.