Дерево Фенвика — различия между версиями
| Строка 79: | Строка 79: | ||
==Преимущества и недостатки дерева Фенвика== | ==Преимущества и недостатки дерева Фенвика== | ||
| − | Главными преимуществами данной конструкции являются простота реализации и быстрота ответов на запросы за <tex> O( | + | Главными преимуществами данной конструкции являются простота реализации и быстрота ответов на запросы за <tex> O(\log{n}) </tex>. Также дерево Фенвика позволяет быстро изменять значения в массиве и находить некоторые функции от элементов массива. |
Недостатком является то, что при изменении одного элемента исходного массива, приходится пересчитывать частичные суммы, а это затратно по времени. | Недостатком является то, что при изменении одного элемента исходного массива, приходится пересчитывать частичные суммы, а это затратно по времени. | ||
Версия 20:17, 26 мая 2015
Дерево Фе́нвика (англ. Binary indexed tree) — структура данных, требующая памяти и позволяющая эффективно (за ) выполнять следующие операции:
- изменять значение любого элемента в массиве,
- выполнять некоторую ассоциативную, коммутативную, обратимую операцию на отрезке .
Впервые описано Питером Фенвиком в 1994 году.
Пусть дан массив . Деревом Фенвика будем называть массив из элементов: , где и — некоторая функция, от выбора которой зависит время работы операций над деревом. Рассмотрим функцию, позволяющую делать операции вставки и изменения элемента за время . Она задается простой формулой: , где — это операция логического . При числа и его значения, увеличенного на единицу, мы получаем это число без последних подряд идущих единиц.
Эту функцию можно вычислять по другой формуле: где — количество подряд идущих единиц в конце бинарной записи числа . Оба варианта равносильны, так как функция, заданная какой-либо из этих формул, заменяет все подряд идущие единицы в конце числа на нули.
Содержание
Запрос изменения элемента
Нам надо научиться быстро изменять частичные суммы в зависимости от того, как изменяются элементы. Рассмотрим как изменяется массив при изменении элемента .
| Лемма: |
Для изменения величины необходимо изменить элементы дерева , для которых верно неравенство . |
| Доказательство: |
| необходимо менять те , для которых попадает в необходимые удовлетворяют условию . |
| Лемма: |
Все такие удовлетворяют равенству , где — это операция побитового логического . |
| Доказательство: |
| Первый элемент последовательности само . Для него выполняется равенство, так как . По формуле мы заменим первый ноль на единицу. Неравенство при этом сохранится, так как осталось прежним или уменьшилось, а увеличилось. Можем заметить, что если количество единиц в конце не будет совпадать с , то формула нарушит неравенство, потому что либо само будет меньше, чем , либо станет больше, чем . Таким образом, перебраны будут только нужные элементы |
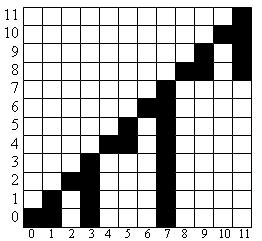
Все мы можем получить следующим образом : . Следующим элементом в последовательности будет элемент, у которого первый с конца ноль превратится в единицу. Можно заметить, что если к исходному элементу прибавить единицу, то необходимый ноль обратится в единицу, но при этом все следующие единицы обнулятся. Чтобы обратно их превратить в единицы, применим операцию . Таким образом все нули в конце превратятся в единицы и мы получим нужный элемент. Для того, чтобы понять, что эта последовательность верна, достаточно посмотреть на таблицу.
Несложно заметить, что данная последовательность строго возрастает и в худшем случае будет применена логарифм раз, так как добавляет каждый раз по одной единице в двоичном разложении числа .
Напишем функцию, которая будет изменять элемент на , и при этом меняет соответствующие частичные суммы.
function modify(i, d):
while i < N
t[i] += d
i = i | (i + 1)
Запрос получения значения функции на префиксе
Пусть существует некоторая бинарная операция . Чтобы получить значение на отрезке , нужно провести операцию, обратную к , над значениями на отрезках и .
В качестве бинарной операции рассмотрим операцию сложения.
Обозначим . Тогда .
| Лемма: |
входит в сумму для , если . |
Для доказательства леммы рассмотрим битовую запись следующих чисел:
Реализация
Приведем код функции :
int sum(i):
result = 0;
while i >= 0
result += t[i]
i = f(i) - 1
return result
Преимущества и недостатки дерева Фенвика
Главными преимуществами данной конструкции являются простота реализации и быстрота ответов на запросы за . Также дерево Фенвика позволяет быстро изменять значения в массиве и находить некоторые функции от элементов массива. Недостатком является то, что при изменении одного элемента исходного массива, приходится пересчитывать частичные суммы, а это затратно по времени.