Шифратор и дешифратор — различия между версиями
Gaporf (обсуждение | вклад) (Метки: правка с мобильного устройства, правка из мобильной версии) |
Gaporf (обсуждение | вклад) (создал новый раздел) (Метки: правка с мобильного устройства, правка из мобильной версии) |
||
| Строка 9: | Строка 9: | ||
|definition='''Шифратор''' (англ. ''encoder'') - логическое устройство, которое имеет $2^n$ входов и $n$ выходов. Если подать сигнал ровно на один вход, то на выходы будут кодировать номер входа, на который подан сигнал. | |definition='''Шифратор''' (англ. ''encoder'') - логическое устройство, которое имеет $2^n$ входов и $n$ выходов. Если подать сигнал ровно на один вход, то на выходы будут кодировать номер входа, на который подан сигнал. | ||
}} | }} | ||
| + | |||
| + | ==Принцип работы дешифратора== | ||
==Логическая схема дешифратора== | ==Логическая схема дешифратора== | ||
Версия 09:49, 17 ноября 2018
Эта статья находится в разработке!
| Определение: |
| Дешифратор (англ. decoder) - логическое устройство, которое имеет $n + 1$ входов и $2^n$ выходов. Обозначим входы как $y_0$, $y_1$, $\ldots$, $y_n$, $x$, а выходы как $z_1$, $z_2$, $\ldots$, $z_{2^n}$. На все выходы подаётся $0$, а на выход $z_i$ подаётся то же, что подаётся на вход $x$, где $i$ - число, которое кодируется входами $y_0$, $y_1$, $\ldots$, $y_n$. |
| Определение: |
| Шифратор (англ. encoder) - логическое устройство, которое имеет $2^n$ входов и $n$ выходов. Если подать сигнал ровно на один вход, то на выходы будут кодировать номер входа, на который подан сигнал. |
Принцип работы дешифратора
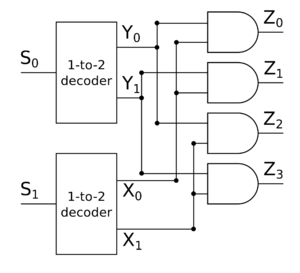
Логическая схема дешифратора
Преимущество дешифратора заключается в том, что размер схемы линейно зависит от входов. Принцип построения такой схемы заключается в том, что мы сначала строим схему для $n-1$ входов, потом пытаемся добавить $n$-ый вход так, чтобы схема оставалась корректной. Заметим, что если на $X$ подать $0$, то на всех выходах $Z_0$, $Z_1$, $\ldots$, $Z_{2^n - 1}$ будет $0$, а если подать $1$, то $1$ должна оказаться только на выходе $Z_i$, где $i$ кодируется входами $S_0$, $S_1$, $\ldots$, $S_{n-1}$. Давайте построим такую схему, чтобы с помощью гейтов $NOT$ и $AND$ у нас получилось ровно $2^n$ различных вариантов значений на входах $S_0$, $S_1$, $\ldots$, $S_{n-1}$.