Интерпретируемые модели

Интерпретируемая модель — модель, обладающая свойством интерпретируемости.

Интерпретируемость — это свойство модели, которое показывает, что структуру данной модели может объяснить человек. При этом структура модели не противоречит данным, на которых данная модель построена, а также она сохраняет некоторые свойства предоставленных данных. При интерпретации модели могут быть объяснены принципы и закономерности, которые использует сама модель для предсказания на конкретных данных.

Практическая польза

Если модель машинного обучения работает хорошо, почему мы просто не доверяем модели и игнорируем факторы, из-за которых она приняла то или иное решение? Проблема в том, что используя только метрику для измерения точности предсказания, возможно такое, что мы решим задачу не полностью или даже не правильно. Нас могут интересовать причины, по которым модель сделала это предсказание.

Например: модель решает, когда нужно класть ковидного больного в палату, а когда отправлять лечиться дома. По статистике люди болеющие астмой выживают чаще, чем здоровые, и логично предположить, что их можно отправлять лечится дома, но дело в том, что этих людей врачи лечат более тщательней, поэтому они и выживают чаще. Если бы мы верили модели в слепую, то люди с астмой просто бы умирали. Поэтому нам важно понять, почему модель пришла к тому или иному выводу.

Когда нужна интерпретируемость

• Когда целью является получение каких-либо знаний с помощью изучения построенной модели.

• Когда алгоритм оптимизировал неполную цель. Например, когда автомобильный инженер получает предсказания о параметрах двигателя, но ему нужно построит в целом достаточно хороший и надёжный автомобиль.

• Для безопасности сложных систем. Такие системы, в большинстве случаев, нельзя протестировать от начала до конца. Вычислительно тяжело просмотреть все возможное входные данные и сценарии развития событий.

Когда интерпретируемость не требуется

• Влияние модели мало, а сама интерпретация требует большого количества ресурсов (предложение новых покупок на основе предыдущих в онлайн магазинах).

• Проблема хорошо разработана, и специалистов обучают ещё в университетах.

• Класс модели широко применяется: линейные модели (стоимость квартиры: понятно, что это метраж, расстояние до метро, школы, детского сада и т.д., но когда параметров много, то уже сложно всё это держать в голове).

• Необходимость скрыть систему (кому давать кредит, качество работы сотрудника, поисковое ранжирование).

Примеры моделей

Пример интерпретируемой модели

Допустим есть модель в банке, которая помогает решить, давать ли кредит человеку или нет. Приходит в банк Вася, модель отказывает ему в кредите, вопрос почему? Интерпретируемая модель ответит, потому что у него, допустим, плохая кредитная история или маленькая зарплата, а по не интерпретируемой модели вряд ли будет что-то понятно.

Пример эффективной в предсказании, но не интерпретируемой модели

Допустим есть данные и задача бинарной классификации, и 99% объектов имеют класс 1, остальные 0. Модель a(x) = 1, имеет точность 99%, но проинтерпретировать ее нельзя для каких-то наших исследований, особенно если нас интересуют, как возникает класс 0. Такая модель не интерпретируема, так как не информативна.

Свойства интерпретируемых моделей

• Предсказуемость и моделируемость: свойства, при которых человек способен предсказывать поведение и ошибки модели, а так же умение "симулировать" их. Например: сложные физические модели, где часто возможно абстрагировать простые правила для примерного предсказания результатов.

• Разложимость и модульность: свойства, при которых человек способен декомпозировать модель на интепретируемые компоненты. Например: деревья решений или линейный модели для небольшой размерности.

• Доверие: пользователь доволен предсказаниями модели, также модель может показать, когда она не совсем уверена в своём предсказании.

• Информативность: из модели можно выявить вспомогательную информацию полезную для принятия какого-либо решения.

• Cтабильность: статистические и оптимизационные свойства

Как создать интерпретируемую модель?

Использовать только интерпретируемые модели (англ. Transparent Models):

рис. 1. Зависимость интерпретируемости от точности.

• Линейные модели.

• Деревья решений, списки правил, наборы правил.

• Модели основывающиеся на предыдущем опыте.

Но не всё хорошо описывается этими моделями.

Построить интерпретируемую модель поверх эмбендинга

Пример: у нас есть лук. Если “лук” находится рядом с “чесноком”, то модель думает о “луке” как об овоще, если “лук” находится рядом с “пистолетом”, “рогаткой”, то модель думает о “луке” как об оружии.

Но модель теперь интерпретируема, но сами признаки перестают быть таковым.

Важность признаков

Одна из возможностей проанализировать модель — оценить, насколько её решение зависит от отдельных признаков.

SHAP — (англ. SHapley Additive exPlanations) Важность i-го признака здесь вычисляется по такой формуле:.

[math]\begin{equation*} \phi_{i}(p) =\sum_{S \subseteq \{1,2..n\} / \{i\}} \frac{|S|!(n - |S| -1)!}{n!}(p(S \cup \{ i \}) - p(S)) \end{equation*}[/math].

где:

[math]p(S \cup \{ i \})[/math] — это предсказание модели с i-тым признаком,

[math]p(S)[/math] — это предсказание модели без i-того признака,

[math]n[/math] — количество признаков,

[math]S[/math] — произвольный набор признаков без i-того признака.

Видно, что вычисление требует обучения модели на всевозможных подмножествах признаках, поэтому на практике применяют приближения формулы.

Суррогатные модели

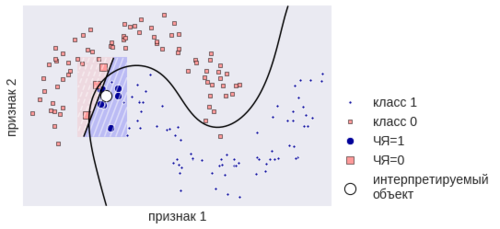
LIME — (англ. Local Interpretable Model-agnostic Explanations) Даже если простая модель не сможет смоделировать сложную во всём пространстве, в окрестности конкретной точки это вполне возможно. Локальные модели объясняют конкретный ответ чёрного ящика. Эта идея показана на рис. 2. У нас есть чёрный ящик (ЧЯ), который построен на данных. В некоторой точке он выдал ответ, мы генерируем выборку в окрестности этой точки, узнаём ответы ЧЯ и настраиваем обычный линейный классификатор. Он описывает ЧЯ в окрестности точки, хотя во всём пространстве он сильно отличается от ЧЯ. Из рис. 2 понятны достоинства и недостатки такого подхода.

рис. 2. Построение локальной суррогатной модели.

См. также

• Уменьшение размерности

• Жизненный цикл модели машинного обучения

Источники информации

• Doshi-Velez and Kim "Towards A Rigorous Science of Interpretable Machine Learning" 2017[5]

• Sanmi Koyejo "Interpretability" MACHINE LEARNING SUMMER SCHOOL 2019 [6]