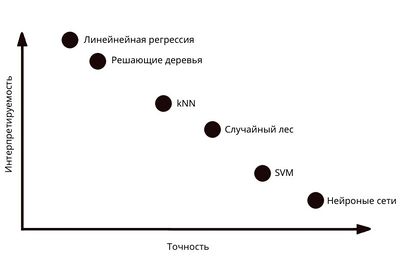
Интерпретируемые модели
Интерпретируемая модель — модель, обладающая свойством интерпретируемости.
Интерпретируемость — это свойство модели, которое показывает, что структуру данной модели может объяснить человек. При этом структура модели не противоречит данным, на которых данная модель построена, а также она сохраняет некоторые свойства предоставленных данных. При интерпретации модели могут быть объяснены принципы и закономерности, которые использует сама модель для предсказания меток класса на конкретных данных.
Практическая польза
Если модель машинного обучения работает хорошо, почему мы просто не доверяем модели и игнорируем факторы, из-за которых она приняла то или иное решение? Проблема в том, что используя только метрику для измерения точности предсказания, возможно такое, что мы решим задачу не полностью или даже не правильно. Нас могут интересовать причины, по которым модель сделала это предсказание.[1]
Например: модель решает, когда нужно класть ковидного больного в палату, а когда отправлять лечиться дома. По статистике люди болеющие астмой выживают чаще, чем здоровые, и логично предположить, что их можно отправлять лечится дома, но дело в том, что этих людей врачи лечат более тщательней, поэтому они и выживают чаще. Если бы мы верили модели в слепую, то люди с астмой просто бы умирали. Поэтому нам важно понять, почему модель пришла к тому или иному выводу.
Когда нужна интерпретируемость
- Когда целью является получение каких-либо знаний с помощью изучения построенной модели.
- Когда алгоритм оптимизировал неполную цель. Например, когда автомобильный инженер получает предсказания о параметрах двигателя, но ему нужно построит в целом достаточно хороший и надёжный автомобиль.
- Для безопасности сложных систем. Такие системы, в большинстве случаев, нельзя протестировать от начала до конца. Вычислительно тяжело просмотреть все возможное входные данные и сценарии развития событий.
- Интерпретация тренировных данных, поиск выбросов в них.
- Поиск ошибок в выводе модели.
- Пользователь может больше доверять модели.
Когда интерпретируемость не требуется
- Влияние модели мало, а сама интерпретация требует большого количества ресурсов (предложение новых покупок на основе предыдущих в онлайн магазинах).
- Проблема хорошо разработана, и специалистов обучают ещё в университетах.
- Класс модели широко применяется: линейные модели (стоимость квартиры: понятно, что это метраж, расстояние до метро, школы, детского сада и т.д., но когда параметров много, то уже сложно всё это держать в голове).
- Необходимость скрыть систему (кому давать кредит, качество работы сотрудника, поисковое ранжирование).
Классификая моделей
- Post-Hoc (воспринимает модель как "черный ящик", например, нейросеть) vs Intrinsic (накладывают ограничения на сложность самой модели).
- Специфические (работают только для конкретной архитектуры модели) vs агностические (можно применить ко всем моделям для решения конкретной задачи).
- Локальные (позволяют понять предсказание для конкретного объекта) vs глобальные (понимание в целом, какие признаки влияют на предсказание).
Примеры моделей
Пример интерпретируемой модели
- Допустим есть модель в банке, которая помогает решить, давать ли кредит человеку или нет. Приходит в банк Вася, модель отказывает ему в кредите, вопрос почему? Интерпретируемая модель ответит, потому что у него, допустим, плохая кредитная история или маленькая зарплата, а по не интерпретируемой модели вряд ли будет что-то понятно.
- Есть данные и задача бинарной классификации, но у нас огромное количество признаков, и мы построили дерево решений для предсказания. И, например, мы заметили, что алгоритм построил нам дерево глубины 1, но при этом точность предсказания очень высока. Это значит, что у нас классы отлично разделимы, только по одному признаку. Это и есть пример хорошей интерпретируемости, смотреть на данные самому достаточно долго, а так же эксперт, работающий с данными, мог не подозревать о том, что для успешной классификации необходим только 1 признак, но проанализировав построенное дерево, все становится очевидно.
Пример эффективной в предсказании, но не интерпретируемой модели
- Допустим есть данные и задача бинарной классификации, и 99% объектов имеют класс 1, остальные 0. Модель a(x) = 1, имеет точность 99%, но проинтерпретировать ее нельзя для каких-то наших исследований, особенно если нас интересуют, как возникает класс 0. Такая модель не интерпретируема, так как не информативна.
- Важным примером, являются данные, в которых присутствует мультиколлинеарность признаков. В таком случае, при обучении линейной модели, мы переобучимся. Для того, чтобы бороться с этой проблемой можно с помощью регуляризации. Но так как, теперь мы оптимизируем несколько другую функцию, то и веса для модели будут отличатся от реальной зависимости на данных, что повлечёт за собой потерю интерпретируемости.
Свойства интерпретируемых моделей
- Предсказуемость и моделируемость: свойства, при которых человек способен предсказывать поведение и ошибки модели, а так же умение "симулировать" их. Например: сложные физические модели, где часто возможно абстрагировать простые правила для примерного предсказания результатов.
- Разложимость и модульность: свойства, при которых человек способен декомпозировать модель на интепретируемые компоненты. Например: деревья решений или линейный модели для небольшой размерности.
- Доверие: пользователь доволен предсказаниями модели, также модель может показать, когда она не совсем уверена в своём предсказании.
- Информативность: из модели можно выявить вспомогательную информацию полезную для принятия какого-либо решения.
- Cтабильность: статистические и оптимизационные свойства
Способы создания интерпретируемой модели
Использовать только интерпретируемые модели
- Линейные модели.
- Деревья решений, списки правил, наборы правил.
- Модели основывающиеся на предыдущем опыте.
Но не всё хорошо описывается этими моделями.
Построить интерпретируемую модель поверх эмбендинга
Пример: у нас есть лук. Если “лук” находится рядом с “чесноком”, то модель думает о “луке” как об овоще, если “лук” находится рядом с “пистолетом”, “рогаткой”, то модель думает о “луке” как об оружии.
Но модель теперь интерпретируема, но сами признаки перестают быть таковым.
Важность признаков
Одна из возможностей проанализировать модель — оценить, насколько её решение зависит от отдельных признаков, какой признак внёс наибольший вес для нахождения решения модели.
Отчётливо это можно понять благодаря следующему примеру. Модель определяет кто на картинке собака или волк. Допустим выборка для обучения оказалось не самой удачной, и все картинки с волками были на снегу, а с собаками на асфальте. Соответственно модель могла начать определять собаку или волка по асфальту или снегу. Благодаря данному виду интерпретации, модель нам можешь сказать, что главным признаком для принятия решения было не само животное, а её окружение.
Данную идею реализуют с помощью значений Шепли.
Значения Шепли (англ. Shapley values) — метод из коалиционной теории игр, который помогает определить, как наиболее честно распределить выигрыш между игроками в зависимости от их вклада в победу. Игроки объединяются в коалиции, чтобы полуучить некоторую выгоду от этого объединения. В машинном обучении в качестве игроков выступают признаки, а в качестве выигрыша — вклад в предсказание. Подходит для задач классификации и регрессии.
Из вклада коалиций рассчитывается вклад каждого признака в итоговый прогноз. Значение Шепли — среднее между маргинальными вкладами всех возможных коалиций[2].
На основе значений Шепли Люндебергом и Ли предложен метод SHAP (SHapley Additive exPlanations), объясняющий индивидуальные предсказания. Доступна его реализация на Python [3].
Важность i-го признака здесь вычисляется по такой формуле:
[4],
где:
— это предсказание модели с i-тым признаком,
— это предсказание модели без i-того признака,
— количество признаков,
— произвольный набор признаков без i-того признака.
Видно, что вычисление требует обучения модели на всевозможных подмножествах признаках, поэтому на практике применяют приближения формулы.
Суррогатные модели
Для интерпретации модели (далее именуемой как черный ящик) можно использовать интерпретируемую суррогатную модель, обученную на выводе черного ящика при различных входных данных. Так как суррогатная модель будет повторять поведение черного ящика, то на её основе можно интерпретировать данный черный ящик.
Есть два типа суррогатных моделей: глобальная и локальная.
- Глобальная суррогатная модель обучена на всем выводе черного ящика. Такая модель полностью повторяет поведение черного ящика, соответственно интерпретирует его на всей выборке.
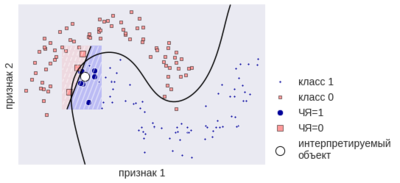
- Локальная суррогатная модель обучена на выводе в какой-то окрестности определенной точки (рис. 2, где ЧЯ — черный ящик). Такая модель зачастую плохо интерпретирует всю выборку, но хорошо справляется с этой задачей в данной окрестности.
Глобальную суррогатную модель довольно сложно построить, поэтому чаще всего прибегают к локальным моделям и интерпретируют определенные объекты.
LIME (англ. Local Interpretable Model-agnostic Explanations) [6] — это библиотека [7], которая строит локальную суррогатную модель.
См. также
Примечания
- ↑ Doshi-Velez and Kim "Towards A Rigorous Science of Interpretable Machine Learning" 2017 Page 5
- ↑ Формулы смотрите здесь [1]
- ↑ Реализация SHAP [2]
- ↑ Павел Трошенков "Как интерпретировать предсказания моделей в SHAP" [3]
- ↑ Александр Дьяконов "Интерпретации чёрных ящиков" Рис.11 [4]
- ↑ Marco Tulio Ribeiro, Sameer Singh, Carlos Guestrin "Explaining the Predictions of Any Classifier" [5]
- ↑ Реализация Lime [6]