Решение RMQ с помощью разреженной таблицы — различия между версиями
Smolcoder (обсуждение | вклад) (→Применение к задаче RMQ) |
Smolcoder (обсуждение | вклад) (→Разреженная таблица) |
||
| Строка 5: | Строка 5: | ||
Разреженная таблица — двумерная структура данных <tex>ST[i, j]</tex>, для которой выполнено следующее: <tex>ST[i,j]=\min\left(A[i], A[i+1], ..., A[i+2^{j}-1]\right),\quad j \in [0 .. \log N]</tex>. Иначе говоря, в этой таблице хранятся минимумы на всех отрезках, длины которых равны степеням двойки. Объём, занимаемый таблицей, равен <tex>O(N \log N)</tex>, и заполненными являются только те элементы, для которых <tex>i+2^j \le N </tex>. | Разреженная таблица — двумерная структура данных <tex>ST[i, j]</tex>, для которой выполнено следующее: <tex>ST[i,j]=\min\left(A[i], A[i+1], ..., A[i+2^{j}-1]\right),\quad j \in [0 .. \log N]</tex>. Иначе говоря, в этой таблице хранятся минимумы на всех отрезках, длины которых равны степеням двойки. Объём, занимаемый таблицей, равен <tex>O(N \log N)</tex>, и заполненными являются только те элементы, для которых <tex>i+2^j \le N </tex>. | ||
| − | Простой метод построения таблицы заключён в следующем реккурентном соотношении: <tex>ST[i | + | Простой метод построения таблицы заключён в следующем реккурентном соотношении: |
| + | <tex> ST[i][j] = | ||
| + | \left\{ | ||
| + | \begin{array}{lcl} | ||
| + | \min\left(ST[i][j-1], ST[i+2^{j-1}][j-1]\right), j > 0 \\ | ||
| + | A[i], j = 0 \\ | ||
| + | \end{array} | ||
| + | \right. | ||
| + | </tex> . | ||
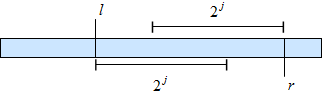
| + | Это достигается за счет идемпотентности операции минимум: <tex>\min(a, a)=a</tex>. Это один из ключевых моментов этого метода, так как идемпотентность позволяет нам корректно считать минимум в области пересечения отрезков. | ||
== Применение к задаче RMQ == | == Применение к задаче RMQ == | ||
Версия 00:37, 26 марта 2012
Разреженная таблица (англ. sparse table) позволяет решать задачу online static RMQ за на запрос, с предподсчётом за и использованием памяти.
Постановка задачи RMQ
Дан массив . Поступают запросы вида , на каждый запрос требуется найти минимум в массиве , начиная с позиции и заканчивая позицией .
Разреженная таблица
Разреженная таблица — двумерная структура данных , для которой выполнено следующее: . Иначе говоря, в этой таблице хранятся минимумы на всех отрезках, длины которых равны степеням двойки. Объём, занимаемый таблицей, равен , и заполненными являются только те элементы, для которых .
Простой метод построения таблицы заключён в следующем реккурентном соотношении: . Это достигается за счет идемпотентности операции минимум: . Это один из ключевых моментов этого метода, так как идемпотентность позволяет нам корректно считать минимум в области пересечения отрезков.
Применение к задаче RMQ
Источники
- Bender, M.A., Farach-Colton, M. et al. — Lowest common ancestors in trees and directed acyclic graphs. — J. Algorithms 57(2) (2005) — с. 75–94.