Решение RMQ с помощью разреженной таблицы
Разреженная таблица (англ. sparse table) позволяет решать задачу online static RMQ (получение минимума или максимума на отрезке, когда элементы массива не могут изменяться, а запросы поступают последовательно) за на запрос, с предподсчётом за и использованием памяти.
| Задача: |
| Дан массив целых чисел. Поступают запросы вида , для каждого из которых требуется найти минимум среди элементов . |
Разреженная таблица
Разреженная таблица — двумерная структура данных , для которой выполнено следующее:
.
Иначе говоря, в этой таблице хранятся минимумы на всех отрезках, длины которых равны степеням двойки. Объём памяти, занимаемый таблицей, равен , и заполненными являются только те элементы, для которых .
Простой метод построения таблицы заключён в следующем рекуррентном соотношении: $$ ST[i][j]= \begin{cases} \min\left(ST[i][j-1], ST[i+2^{j-1}][j-1]\right),&\text{если $j > 0$;}\\ A[i], &\text{если $j = 0$;} \end{cases} $$
Идемпотентность
Такая простота достигается за счет идемпотентности операции минимум: . Это один из ключевых моментов этого метода, так как она позволяет нам корректно считать минимум в области пересечения отрезков.
Пусть $\circ$ — произвольная бинарная операция, которая удовлетворяет свойствам:
- ассоциативности: $a \circ (b \circ c) = (a \circ b) \circ c $,
- коммутативности: $a \circ b = b \circ a$,
- идемпотентности: $a \circ a = a $.
| Утверждение: |
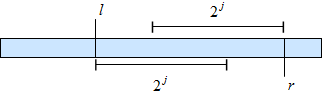
$a_l \circ a_{l+1} \circ \ldots \circ a_r = (a_l \circ a_{l+1} \circ \ldots \circ a_{l + k}) \circ (a_{r - k} \circ a_{r - k + 1} \circ \ldots \circ a_r)$, где $\frac{r - l}{2} \leqslant k \leqslant r - l$. |
| Отрезок $(a_{r-k}, a_{l + k})$ содержится в обоих операндах правой части. Значит, каждый элемент из него входит два раза. По коммутативности мы можем располагать элементы в любом порядке, по ассоциативности мы можем выполнять операции в произвольном порядке, поэтому повторяющие в правой части элементы мы можем расположить рядом друг с другом и затем по идемпотентности один из них убрать. Переставляя оставшиеся элементы в правой затем легко получаем выражение в левой части. |
Применение к задаче RMQ
int fl(int len):
if len 1
return 0
else
return fl() + 1
Вычисление происходит за . А так как длина может принимать различных значений, то суммарное время предпосчета составляет .
Пусть теперь дан запрос . Заметим, что , где , то есть логарифм длины запрашиваемого отрезка, округленный вниз. Но эту величину мы уже предпосчитали, поэтому запрос выполняется за .
Из выше доказанной теоремы следует, что этот метод работает не только с операцией минимум, но и с любой идемпотентной, ассоциативной и коммутативной операцией. Таким образом мы получаем целый класс задач, решаемых разреженной таблицей.
См. также
- Сведение задачи LCA к задаче RMQ
- Алгоритм Фарака-Колтона и Бендера
- Сведение задачи RMQ к задаче LCA
- Heavy-light декомпозиция
Источники информации
- Bender, M.A., Farach-Colton, M. et al. — Lowest common ancestors in trees and directed acyclic graphs. — J. Algorithms 57(2) (2005) — с. 75–94.