Шифратор и дешифратор — различия между версиями
Gaporf (обсуждение | вклад) (Метки: правка с мобильного устройства, правка из мобильной версии) |
Gaporf (обсуждение | вклад) (Метки: правка с мобильного устройства, правка из мобильной версии) |
||
| Строка 3: | Строка 3: | ||
{{Определение | {{Определение | ||
| − | |definition='''Дешифратор''' (англ. ''decoder'') - логический элемент, | + | |definition='''Дешифратор''' (англ. ''decoder'') - логический элемент, имеющий $n$ входов $s_0$, $s_1$, $\ldots$, $s_{n-1}$ и $2^n$ выходов $z_0$, $z_1$, $\ldots$, $z_{2^n-1}$. На все выходы подаётся $0$, кроме выхода $z_i$, на который подаётся $1$, где $i$ - число, которое закодировано входами $s_0$, $s_1$, $\ldots$, $s_{n-1}$ |
}} | }} | ||
==Принцип работы== | ==Принцип работы== | ||
| − | Для | + | Суть дешифратора заключается в том, что с помощью $n$ входов $s_0$, $s_1$, $\ldots$, $s_{n-1}$ можно управлять, на какой выход будет подаваться $1$. Для того, чтобы лучше понять, как работает дешифратор, рассмотрим дешифратор 2-to-4 (это значит, что у этого дешифратора есть два входа $s_0$ и $s_1$ и четыре выхода $z_0$, $z_1$, $z_2$ и $z_3$). Если $s_0 = s_1 = 0$, то на выходе $z_0$ будет значение $1$, на остальных выходах будет $0$. Если же $s_0 = 1$ и $s_1 = 0$, то на выходе $z_1$ будет $1$, на остальных выходах будут $0$. Если $s_0 = 0$ и $s _1 = 1$, то на выходе $z_2$ будет $1$, а на остальных входах будет $0$. Если же $s_0 = s_1 = 1$, то на выходе $z_3$ будет $1$, а на других - $0$. Для более ясной картины обратимся к таблице истинности. |
{| class="wikitable" | {| class="wikitable" | ||
| Строка 25: | Строка 25: | ||
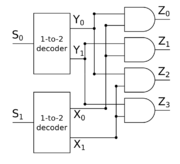
[[Файл:LogicSircuit2to4decoder.png|thumb|180px|Логическая схема дешифратора 2-to-4]] | [[Файл:LogicSircuit2to4decoder.png|thumb|180px|Логическая схема дешифратора 2-to-4]] | ||
| − | + | Давайте переберём всевозможные варианты значений на входах. Поскольку у нас $n$ входов, то отсюда следует, что всевозможных вариантов - $2^n$. Давайте будем строить такую схему рекурсивным способом, т.е. сначала построим дешифратор для $n-1$ элемента, а потом сольём $n$-ый элемент с $n-1$ элементами. Допустим, что $n = 1$. Тогда очевидно, что всевозможных вариантов всего два: $s_0 = 0$ или $s_0 = 1$. Давайте от входа $s_0$ мы выведем два провода, один из них, пока, не будем трогать, а другой соединим с гейтом $NOT$. Если количество входов было равно $1$, то мы перебрали всевозможные варианты, т.е. давайте соединим провод без гейта $NOT$ с выходом $z_0$, а с гейтом $NOT$ - с выходом $z_1$. Допустим, что $n \geqslant 2$. Тогда допустим, что мы построили дешифратор для $n-1$ элемента. Теперь сольём $n$-ый вход с дешифратором для $n-1$ входов. У такого дешифратора $2^{n-1}$ выходов. У входа $s_{n-1}$ может быть два варианта значений: $0$ и $1$. Давайте поставим $2^n$ гейтов $AND$ и соединим эти гейты соответственно с выходами дешифратора ${n-1}$-to-${2^{n-1}}$. | |
Версия 00:24, 20 ноября 2018
| Определение: |
| Дешифратор (англ. decoder) - логический элемент, имеющий $n$ входов $s_0$, $s_1$, $\ldots$, $s_{n-1}$ и $2^n$ выходов $z_0$, $z_1$, $\ldots$, $z_{2^n-1}$. На все выходы подаётся $0$, кроме выхода $z_i$, на который подаётся $1$, где $i$ - число, которое закодировано входами $s_0$, $s_1$, $\ldots$, $s_{n-1}$ |
Принцип работы
Суть дешифратора заключается в том, что с помощью $n$ входов $s_0$, $s_1$, $\ldots$, $s_{n-1}$ можно управлять, на какой выход будет подаваться $1$. Для того, чтобы лучше понять, как работает дешифратор, рассмотрим дешифратор 2-to-4 (это значит, что у этого дешифратора есть два входа $s_0$ и $s_1$ и четыре выхода $z_0$, $z_1$, $z_2$ и $z_3$). Если $s_0 = s_1 = 0$, то на выходе $z_0$ будет значение $1$, на остальных выходах будет $0$. Если же $s_0 = 1$ и $s_1 = 0$, то на выходе $z_1$ будет $1$, на остальных выходах будут $0$. Если $s_0 = 0$ и $s _1 = 1$, то на выходе $z_2$ будет $1$, а на остальных входах будет $0$. Если же $s_0 = s_1 = 1$, то на выходе $z_3$ будет $1$, а на других - $0$. Для более ясной картины обратимся к таблице истинности.
| $S_0$ | $S_1$ | $Z_0$ | $Z_1$ | $Z_2$ | $Z_3$ |
|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 |
Логическая схема
Давайте переберём всевозможные варианты значений на входах. Поскольку у нас $n$ входов, то отсюда следует, что всевозможных вариантов - $2^n$. Давайте будем строить такую схему рекурсивным способом, т.е. сначала построим дешифратор для $n-1$ элемента, а потом сольём $n$-ый элемент с $n-1$ элементами. Допустим, что $n = 1$. Тогда очевидно, что всевозможных вариантов всего два: $s_0 = 0$ или $s_0 = 1$. Давайте от входа $s_0$ мы выведем два провода, один из них, пока, не будем трогать, а другой соединим с гейтом $NOT$. Если количество входов было равно $1$, то мы перебрали всевозможные варианты, т.е. давайте соединим провод без гейта $NOT$ с выходом $z_0$, а с гейтом $NOT$ - с выходом $z_1$. Допустим, что $n \geqslant 2$. Тогда допустим, что мы построили дешифратор для $n-1$ элемента. Теперь сольём $n$-ый вход с дешифратором для $n-1$ входов. У такого дешифратора $2^{n-1}$ выходов. У входа $s_{n-1}$ может быть два варианта значений: $0$ и $1$. Давайте поставим $2^n$ гейтов $AND$ и соединим эти гейты соответственно с выходами дешифратора ${n-1}$-to-${2^{n-1}}$.