Список — различия между версиями
(→Вставка) |
(→Поиск) |
||
| Строка 15: | Строка 15: | ||
==Операции в связном списке== | ==Операции в связном списке== | ||
===Поиск=== | ===Поиск=== | ||
| − | + | find(k) | |
{ | { | ||
| − | + | x = head; | |
| − | + | while ((x->key != k)&&(x != NULL)) | |
| − | + | x = x -> next; | |
| − | + | return x; | |
} | } | ||
Поиск в худшем случае выполняется за <math>\Theta(n)</math>, так как может понадобиться просмотреть весь список. | Поиск в худшем случае выполняется за <math>\Theta(n)</math>, так как может понадобиться просмотреть весь список. | ||
| + | |||
===Вставка=== | ===Вставка=== | ||
insert(k) | insert(k) | ||
Версия 23:39, 3 мая 2011
Связный список - структура данных, состоящая из узлов, содержащих помимо собственных данных ссылки на следующий или предыдущий узел списка. С помощью списков можно реализовать такие структуры данных как стек и очередь. Вставка и удаление в списке работают за O(1).
Содержание
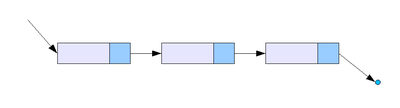
Односвязный список
Простейшай реализация списка. В узлах хранятся данные и указатель на следующий элемент в списке.
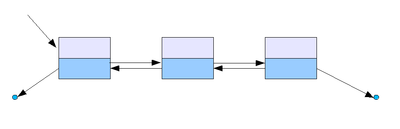
Двусвязный список
Также хранится указатель на предыдущий элемент списка, благодаря чему становится проще удалять и переставлять элементы.
XOR-связный список
XOR-связный список — структура данных, похожая на обычный двусвязный список, однако в каждом элементе хранящая только один адрес — результат выполнения операции XOR над адресами предыдущего и следующего элементов списка. Для того, чтобы перемещаться по списку, необходимо взять два последовательных адреса и выполнить над ними операцию XOR, которая и даст реальный адрес следующего элемента.
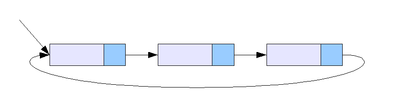
Циклический список
Первый элемент является следующим для последнего элемента списка.
Операции в связном списке
Поиск
find(k)
{
x = head;
while ((x->key != k)&&(x != NULL))
x = x -> next;
return x;
}
Поиск в худшем случае выполняется за , так как может понадобиться просмотреть весь список.
Вставка
insert(k)
{
tmp = head;
x->key = k;
x->next = tmp;
head = x;
}
Время работы вставки O(1).
Удаление
delete(k)
{
tmp = find(k);
if (tmp != NULL)
{
//освобождаем память
tmp = tmp->next;
}
}
Само удаление работает за O(1), но если требуется сначала найти удаляемый элемент, то на поиск + удаление потребуется времени.
См.также
Массив с увеличением/уменьшением размера
Ссылки
http://en.wikipedia.org/wiki/Linked_list Linked list
Литература
- Т. Кормен, Ч. Лейзерсон, Р. Ривест: Алгоритмы: построение и анализ глава 11.2
- Д. Кнут: Искусство программирования том 1 глава 2.2