Очередь
Содержание
Определение
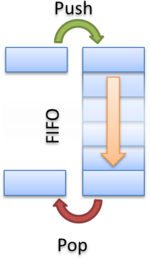
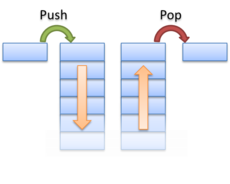
Очередь (англ. queue) — это структура данных, добавление и удаление элементов в которой происходит путём операций и соответственно. Притом первым из очереди удаляется элемент, который был помещен туда первым, то есть в очереди реализуется принцип «первым вошел — первым вышел» (first-in, first-out — FIFO). У очереди имеется голова (head) и хвост (tail). Когда элемент ставится в очередь, он занимает место в её хвосте. Из очереди всегда выводится элемент, который находится в ее голове.
- (запись в очередь) — операция вставки нового элемента.
- (снятие с очереди) — операция удаления нового элемента.
- — проверка очереди на наличие в ней элементов
Реализация циклической очереди на массиве
Очередь, способную вместить не более элементов, можно реализовать с помощью массива . Она будет обладать следующими полями:
- (голова очереди)
- (хвост очереди)
- (размер очереди)
push
function push(x): elements[tail] = x tail = (tail + 1) % elements.length
pop
T pop():
if not empty()
x = elements[head]
head = (head + 1) % elements.length
return x
empty
boolean empty(): return head == tail
Из-за того что нам не нужно перевыделять память, каждая операция выполняется за времени.
Плюсы:
- прост в разработке
- по сравнению с реализацией на списке, есть незначительная экономия памяти
Минусы:
- количество элементов в очереди ограничено размером массива (исправляется написанием функции расширения массива)
- при переполнении очереди требуется перевыделение памяти и копирование всех элементов в новый массив
Реализация на списке
Для данной реализации очереди необходимо создать список () и операции работы на созданном списке.
Реализация очереди на односвязном списке:
list
- — поле, в котором хранится значение элемента
- — указатель на следующий элемент очереди
push
function push(x):
element = tail
tail = new list(x, NULL)
if size == 0
head = tail
else
element.next = tail
pop
T pop():
if empty()
return
element = head
head = head.next
return element
empty
boolean empty(): return head == tail
Каждая операция выполняется за время .
Минусы:
- Память фрагментируется гораздо сильнее и последовательная итерация по такой очереди может быть ощутимо медленнее, нежели итерация по очереди реализованной на массиве
Реализация на двух стеках
Эта реализация пригодится, например, для нахождения наименьшего элемента за . Очередь можно реализовать на двух стеках и . Один из стеков будем использовать для операции , другой для операции . При этом, если при попытке извлечения элемента из он оказался пустым, просто перенесем все элементы из в него (при этом элементы в получатся уже в обратном порядке, что нам и нужно для извлечения элементов, а станет пустым).
- и — функции, реализующие операцию для соответствующего стека;
- и — аналогично операции .
push
function push(x): pushLeft(x)
pop
T pop():
if not rigthStack.empty()
return popRight()
else
while not leftStack.empty()
pushRight(popLeft())
return popRight()
При выполнении операции будем использовать три монеты: одну для самой операции, вторую в качестве резерва на операцию из первого стека, третью во второй стек на финальный . Тогда для операций учётную стоимость можно принять равной нулю и использовать для операции монеты, оставшиеся после операции .
Таким образом, для каждой операции требуется монет, а значит, амортизационная стоимость операций .
Минусы:
- Если не пуст, то операция может выполняться времени, в отличии от других реализаций, где всегда выполняется за
Реализация на шести стеках
Одним из минусов реализации на двух стеках является то, что в худшем случае мы тратим времени на операцию. Если распределить время, необходимое для перемещения элементов из одного стека в другой, по операциям, мы получим очередь без худших случаев с истинного времени на операцию.
Подробное описание в статье Персистентная очередь.
Отличия от других реализаций
Плюсы:
- реального времени на операцию.
- Возможность дальнейшего улучшения до персистентной очереди, если использовать персистентные стеки.
Минусы:
- Дольше в среднем выполняются операции.
- Больше расход памяти.
- Большая сложность реализации.
См. также
Ссылки
- Википедия — Очередь (программирование)
- Т. Кормен. «Алгоритмы. Построение и анализ» второе издание, Глава 10.1, стр. 262
- T. H. Cormen. «Introduction to Algorithms» third edition, Chapter 10.1, p. 262
- Hood R., Melville R. Real Time Queue Operations in Pure LISP. — Cornell University, 1980