Автоматы Мура и Мили

Определение:

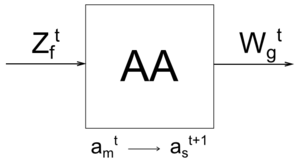
Абстрактный автомат (АА) является математической моделью дискретного устройства и описывается шестикомпонентным набором [math]S=(A, Z, W, \delta, \lambda, a_{1})[/math], где 1. [math]A=\{a_{1}, ..., a_{m}, ..., a_{M}\}[/math] - множество состояний. 2. [math]Z=\{z_{1}, ..., z_{f}, ..., z_{F}\}[/math] - множество входных сигналов. 3. [math]W=\{w_{1}, ..., w_{g}, ..., w_{G}\}[/math] - множество выходных сигналов. 4. [math]\delta[/math] - функция переходов АА, которая некоторым парам \<состояние - входной сигнал\> ([math]a_{m}[/math], [math]z_{f}[/math]) ставит в соответствие состояние АА [math]a_{s}[/math], т.е. [math]a_{s} = δ(a_{m}, z_{f})[/math], [math]a_{s}\in A[/math]. 5. [math]\lambda[/math] - функция выходов АА, которая некоторым парам \<состояние – входной сигнал\> ([math]a_{m}[/math], [math]z_{f}[/math]) ставит в соответствие выходной сигнал АА [math]w_{g}[/math], т.е. [math]w_{g}=λ(a_{m},z_{f})[/math], [math]w_{g}\in W[/math]. 6. [math]a_{1}[/math] - начальное состояние. АА работает в дискретные моменты времени, и в момент времени [math]t=0[/math] автомат всегда находится в состоянии [math]a_{1}[/math].

Рис. 1. Работа АА

Выходные сигналы АА зависят от того, что поступало на его вход раньше.

В каждый момент времени АА, будучи в состоянии [math]a_{m}^{t}[/math], способен воспринимать одну из букв входного алфавита [math]z_{f}^{t}[/math]. В соответствии с функцией [math]\delta[/math], АА перейдет в состояние [math]a_{1}^{t+1}[/math] с выдачей выходного сигнала, который вырабатывается в соответствии с функцией выходов [math]\lambda[/math].

Рассмотрим функционирование автоматов Мура и Мили.

Автомат Мили [math]a(t+1) = \delta (a(t), z(t))[/math] [math]w(t) = \lambda (a(t), z(t))[/math]

Автомат Мура [math]a(t+1) = \delta (a(t), z(t))[/math] [math]w(t) = \lambda (a(t))[/math]

В автоматах Мура выходной сигнал определяется только состоянием автомата в какой-то момент времени и не зависит от входного сигнала в этот же момент времени.

 

Способы задания автоматов

Табличный способ задания автомата Мили

Автомат Мили может быть задан таблицей переходов и таблицей выходов.

В таблице переходов АА Мили на пересечении столбца [math]a_{m}[/math] и строки [math]z_{f}[/math] записывается состояние [math]a_{s}[/math], которое есть функция [math]\delta[/math] от [math]a_{m}[/math] и [math]z_{f}[/math]

	[math]a_{m}[/math]
[math]z_{f}[/math]	[math]a_{s}[/math]	[math]=\delta (a_{m}, z_{f})[/math]

В таблице выходов на пересечении столбца [math]a_{m}[/math] и строки [math]z_{f}[/math] записывается выходной сигнал, который есть функция [math]\lambda[/math] от [math]a_{m}[/math] и [math]z_{f}[/math].

	[math]a_{m}[/math]
[math]z_{f}[/math]	[math]w_{g}[/math]	[math]=\lambda (a_{m}, z_{f})[/math]

Пример: Задание автомата Мили табличным способом (автомат имеет два входных сигнала, два выходных сигнала и три состояния).

Таблица переходов [math]\delta[/math] [math]a_{1}[/math] [math]a_{2}[/math] [math]a_{3}[/math] [math]z_{1}[/math] [math]a_{1}[/math] [math]a_{3}[/math] [math]a_{1}[/math] [math]z_{2}[/math] [math]a_{2}[/math] [math]a_{1}[/math] [math]a_{2}[/math]

Таблица выходов [math]\lambda[/math] [math]a_{1}[/math] [math]a_{2}[/math] [math]a_{3}[/math] [math]z_{1}[/math] [math]w_{2}[/math] [math]w_{2}[/math] [math]w_{2}[/math] [math]z_{2}[/math] [math]w_{1}[/math] [math]w_{1}[/math] [math]w_{2}[/math]

Графический способ задания автомата Мили

Рис. 2. Графическое задание автомата Мили

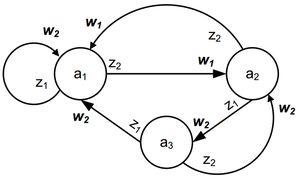
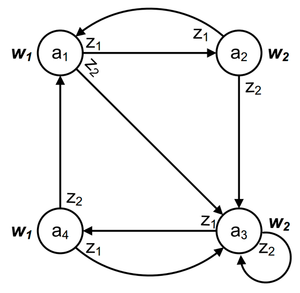
На рисунке (рис. 2) приведен граф автомата Мили на 3 состояния, имеющий 2 входных сигнала и 2 выходных сигнала (см. предыдущий пример).

Табличный способ задания автомата Мура

В автомате Мура выходной сигнал зависит только от состояния автомата и не зависит от входного сигнала.

Поэтому достаточно для задания автомата Мура в таблице переходов добавить одну строку.

[math]\lambda[/math]	[math]w_{1}[/math]	[math]w_{2}[/math]	[math]w_{1}[/math]	[math]w_{2}[/math]	[math]w_{2}[/math]
[math]\delta[/math]	[math]a_{1}[/math]	[math]a_{2}[/math]	[math]a_{3}[/math]	[math]a_{4}[/math]	[math]a_{5}[/math]
[math]z_{1}[/math]	[math]a_{2}[/math]	[math]a_{2}[/math]	[math]a_{5}[/math]	[math]a_{5}[/math]	[math]a_{2}[/math]
[math]z_{2}[/math]	[math]a_{3}[/math]	[math]a_{3}[/math]	[math]a_{1}[/math]	[math]a_{1}[/math]	[math]a_{4}[/math]

Графический способ задания автомата Мура

Рис. 3. Графическое задание автомата Мура

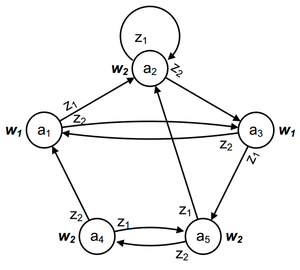
На рисунке (рис. 3) приведен граф автомата Мура на 5 состояний, имеющий 2 входных сигнала и 2 выходных сигнала.

Реакция автоматов на входное слово

Автомат Мили

Рис. 4. Реакция автомата Мили на входное слово

Допустим, входное слово [math]\xi[/math] поступает на вход автомата буква за буквой.

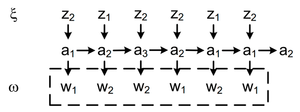
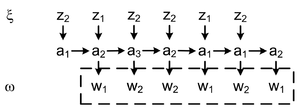
Выходное слово [math]\omega[/math] называется реакцией автомата Мили на входное слово [math]\xi[/math] в состоянии [math]a_{1}[/math] (рис. 4; строится по таблице переходов и выходов).

Реакцию автомата на входное слово [math]\xi[/math] можно заменить обходом графа.

Автомат Мура

Рис. 5. Реакция автомата Мура на входное слово

Выходное слово [math]\omega[/math] называется реакцией автомата Мура на входное слово [math]\xi[/math] в состоянии [math]a_{1}[/math] (рис. 5).

В рассматриваемом примере для автоматов Мили и Мура реакции автоматов на одинаковое входное слово совпадают, но они сдвинуты на один такт. Автоматы Мили и Мура дающие одинаковые реакции на одинаковые входные слова называются эквивалентными. Данное замечание приводит к задаче построения эквивалентных автоматов, дающих одинаковые реакции на одинаковые входные слова.

Эквивалентность автоматов Мили и Мура

Опишем алгоритмы взаимной трансформации моделей Мили и Мура. При этом в автоматах Мура будем пренебрегать выходным сигналом [math]\lambda(a_{1})[/math], связанным с начальным состоянием.

Переход от автомата Мура к автомату Мили

Шестикомпонентным набором с индексом А будем обозначать автомат Мура, а с индексом В - автомат Мили.

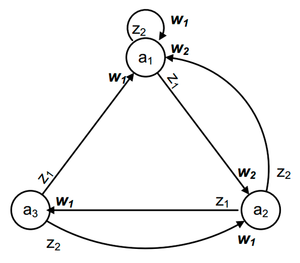
Пусть задан автомат Мура (рис. 6).

Рис.6 Автомат Мура

Требуется перейти к автомату Мили

[math]S_{B} = (A_{B}, Z_{B}, W_{B}, \delta _{B}, \lambda _{B}, a_{1B}[/math]),

у которого [math]Z_{A} = Z_{B}[/math], [math]W_{A} = W_{B}[/math], т.е. входные и выходные алфавиты совпадают.

Рассмотрим пример, в котором [math]Z_{А} = \{z_{1}, z_{2}\} = Z_{B}[/math], [math]W_{A} = \{w_{1}, w_{2}\} = W_{B}[/math], [math]a_{1A} = a_{1B}[/math], алфавит состояний автомата Мура содержит четыре элемента.

При переходе от автомата Мура к автомату Мили алфавиты состояний также совпадают, т.е. [math]A_{A} = A_{B}[/math].

Для определения соответствия между функциями переходов выходов автоматов Мура и Мили воспользуемся следующей вспомогательной таблицей.

Мура	Мили
[math]\delta _{A} (a_{m}, z_{f}) = a_{s}[/math]	[math]\delta _{B} (a_{m}, z_{f}) = a_{s}[/math]
[math]\lambda _{A}(a_{m}) = w_{g}[/math]	[math]\lambda _{B} (a_{m}, z_{f}) = w_{g}[/math]

При переходе от автомата Мура к автомату Мили функции переходов также совпадают, а для определения функции выходов выходные сигналы с вершин опускается на входные дуги.

Проделав такие преобразования мы должны доказать, что получили автомат Мили, эквивалентный автомату Мура, т.е. что реакции автоматов на одинаковые входные воздействия совпадают.

При таком переходе (Мура к Мили) число состояний совпадает.

Утверждение:

Полученный автомат эквивалентен исходному

[math]\triangleright[/math]

Пусть символ [math]z_{f}[/math] поступает на вход автомата Мура [math]S_{A}[/math], который находится в состоянии [math]a_{m}[/math]. Следовательно, [math]S_{A}[/math] перейдет в состояние [math]a_{s} = \delta _{A}(a_{m}, z_{f})[/math] и выдаст сигнал [math]w_{g} = \lambda _{A}(a_{s})[/math]. Соответствующий автомат Мили [math]S_{B}[/math] из состояния [math]a_{m}[/math] также перейдет в состояние [math]a_{s} = \delta _{B}(a_{m}, z_{f}) = \delta _{A}(a_{m}, z_{f})[/math] и выдаст тот же сигнал [math]w_{g} = \lambda _{B}(a_{m}, z_{f}) = \lambda _{A}(\delta _{A}(a_{m}, z_{f})) = \lambda _{A}(a_{s}) = w_{g}[/math]. Таким образом, для выходной последовательности длины 1 поведение автоматов [math]S_{1}[/math] и [math]S_{2}[/math] полностью совпадает. Далее по индукции получаем эквивалентность автоматов.

[math]\triangleleft[/math]

Переход от автомата Мили к автомату Мура

Рис. 7. Автомат Мили

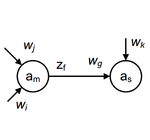
Пусть задан автомат Мили [math]S_{B} = (A_{B}, Z_{B}, W_{B}, \delta _{B}, \lambda _{B}, a_{1B})[/math] (рис. 7).

Требуется перейти к автомату Мура [math]S_{A} = (A_{A}, Z_{A}, W_{A}, \delta _{A}, \lambda _{A}, a_{1A})[/math], у которого [math]Z_{B} = Z_{A}[/math]; [math]W_{B} = W_{A}[/math], т.е. входные и выходные алфавиты совпадают.

Рассмотрим пример, в котором [math]Z_{B} = \{z_{1}, z_{2}\} = Z_{А}[/math], [math]W_{B} = \{w_{1}, w_{2}\} = W_{A}[/math], алфавит состояний автомата Мили содержит три элемента.

Для определения алфавита состояний, функций переходов и выходов автомата Мура воспользуемся следующей вспомогательной таблицей.

Мура	Мили

В данном случае [math]A_{B} \neq A_{A}[/math].

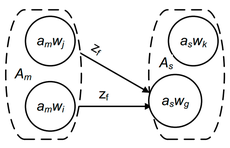
При таком переходе (Мили к Мура) каждому состоянию автомата Мили [math]a_{s}[/math] ставится в соответствие множество всевозможных пар [math]a_{s} \rightarrow A_{s} = \{( a_{s}, w_{g}) | a_{s} = \delta(a_{m}, z_{f}), w_{g} = \lambda(a_{m}, z_{f})\}[/math], где [math]a_{s}[/math] есть функция [math]\delta[/math] от состояния и входного сигнала, [math]w_{g}[/math] функция [math]\lambda[/math] от состояния и входного сигнала.

Пример:

Мура	Мили
	[math]A_{s} = \{(a_{s}, w_{1}), (a_{s}, w_{2}), (a_{s}, w_{3})\}[/math]

Для состояния:

[math]a_{1}: A_{1} = \left \{ \begin {array} {crl} (a_{1}, w_{1}) = b_{1} \\ (a_{1}, w_{2}) = b_{2} \\ \end {array} \right.[/math]

[math]a_{2}: A_{1} = \left \{ \begin {array} {crl} (a_{2}, w_{1}) = b_{3} \\ (a_{2}, w_{2}) = b_{4} \\ \end {array} \right.[/math]

[math]a_{3}: A_{3} = \{ (a_{3}, w_{1}) \} = b_{5}[/math]

В качестве начального состояния результирующего автомата может быть выбрано любое состояние Мура, порожденное начальным состоянием автомата Мили, т.е. состояния [math]b_{1}[/math] или [math]b_{2}[/math].

При определении функции переходов результирующего автомата Мура из всех состояний, порожденных одним состоянием автомата Мили, должны быть переходы под воздействием одинаковых входных сигналов.

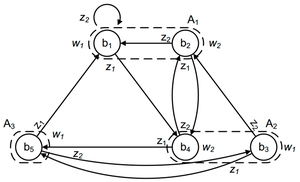
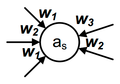
Поскольку в автомате Мура выходной сигнал зависит только от состояния автомата, то в примере рядом с состояниями проставим соответствующие выходные сигналы (рис. 8).

Рис. 8. Выходные сигналы автомата Мура

И так если осуществить следующие преобразования, то получим:

Мили	Мура	Мили
[math]S_{1} \rightarrow[/math]	[math]S_{2} \rightarrow[/math]	[math]S_{3}[/math]
3 состояния	5 состояний	5 состояний

Можно утверждать, что если [math]S_{1}[/math] эквивалентно [math]S_{2}[/math], а [math]S_{2}[/math] эквивалентно [math]S_{3}[/math], то [math]S_{1}[/math] эквивалентно [math]S_{3}[/math] (т.е. эквивалентность обладает свойством транзитивности).

Доказательство эквивалентности автоматов [math]S_{A}[/math] и [math]S_{B}[/math] аналогично предыдущему случаю.

Методы взаимной транспозиции автоматов Мили и Мура показывают, что при переходе от автомата Мили к автомату Мура число состояний принципиально не меняется. В то время как при обратном переходе в автомат Мура число состояний, как правило, увеличивается. Вследствие транзитивности отношения эквивалентности два автомата Мили, первый из которых получен из автомата Мура, так же будут эквивалентны, но у второго автомата число состояний будет больше. Таким образом эквивалентные между собой автоматы могут иметь различное число состояний. В связи с чем и возникает задача нахождения минимального автомата в классе эквивалентных между собой автоматов. Существование для любого абстрактного автомата эквивалентного ему абстрактного автомата с минимальным числом внутренних состояний впервые было доказано Муром.

Ссылки

• Абстрактные автоматы
• [https://ru.wikipedia.org/wiki/Автомат_Мура Автомат Мура
• Теория автоматов
• Синтез дискретных автоматов