Автоматы Мура и Мили
| Определение: |
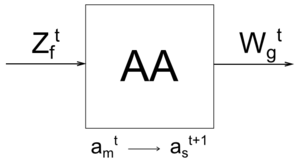
Абстрактный автомат (англ. Abstract Machine) является математической моделью дискретного устройства и описывается шестикомпонентным набором , где
|
Выходные сигналы АА зависят от того, что поступало на его вход раньше.
В каждый момент времени АА, будучи в состоянии , способен воспринимать одну из букв входного алфавита . В соответствии с функцией , АА перейдет в состояние с выдачей выходного сигнала, который вырабатывается в соответствии с функцией выходов .
Рассмотрим функционирование автоматов Мура и Мили.
|
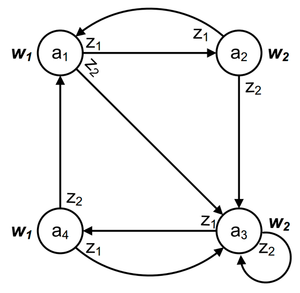
Автомат Мили
|
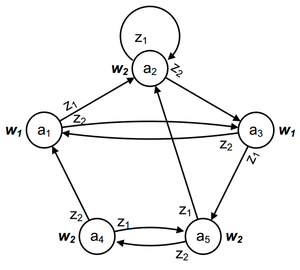
Автомат Мура
|
В автоматах Мура выходные воздействия записаны на состояниях, а в автомате Мили — на переходах.
Применение автоматов Мура и Мили
Автоматы Мура и Мили широко применяются при проектировании цифровых устройств на основе программируемых логических интегральных схем (ПЛИС).
Основное преимущество использования автомата Мили заключается в возможности реакции автомата в течение текущего такта, что обусловлено зависимостью текущей выходной комбинации от текущей входной комбинации .
Наличие минимальной выходной задержки, связанной с переключением выходного регистра, отсутствие нестабильности переходного процесса на выходе автомата, отсутствие сквозного распространения сигнала через комбинационную схему от входа до выхода автомата, простота описания на языках описания аппаратуры HDL делает автомат Мура практически незаменимым.
Также автоматы Мура и взаимодействующие автоматы Мили используются в генетическом программировании (например, для решения задачи об "Умном муравье" [1]).
Автомат, регулирующий пешеходный переход
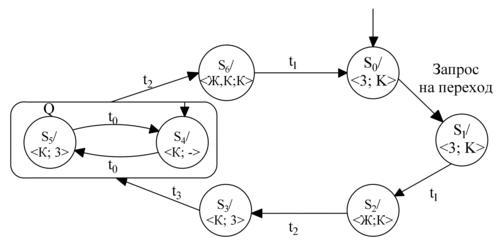
Рассмотрим автомат, регулирующий пешеходный переход по запросу пешеходов. Внешние события автомата — это события нажатия пешеходами кнопки-запроса на тротуаре и исчерпание тайм-аута. Автомат строится как автомат Мура, в котором выход — регулирование светофора и разрешающий сигнал на переход — это потенциальные сигналы, являющиеся функциями состояния.
Выход автомата в каждом состоянии определяется парой Светофор транспорта; светофор пешехода. Например, в состоянии управляющий автомат устанавливает З; К, то есть включёнными зеленый свет транспорту и красный — пешеходам. В состоянии установлен Ж, К; К, то есть желтый и красный свет транспорту (приготовиться) и красный — пешеходам. В начальном состоянии разрешен проезд транспорту, а пешеходам движение запрещено.
В состояниях , при запрещающем сигнале транспорту зеленый сигнал пешеходам мигает каждые секунд в течение секунд. Запрос на переход принимается только в состоянии , в остальных состояниях он игнорируется. Задержки (тайм-ауты — ) устанавливаются в момент перехода автомата в данное состояние, по исчерпании тайм-аута автомат переходит в следующее состояние. В гиперсостоянии , объединяющему пару состояний и , автомат находится ровно секунд: внутренние переходы не срывают тайм-аута.
Именно для этого удобно использовать гиперсостояние .
Торговый автомат
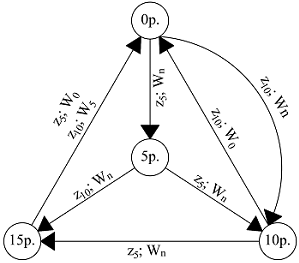
В качестве примера применения автомата Мили рассмотрим автомат по продаже шоколадок стоимостью рублей, принимающий монеты номиналом в и рублей и возвращающий сдачу, если это необходимо.
Состояний автомата всего четыре: , , и рублей.
Входных сигналов два: — рублей и — рублей.
Выходных сигналов три: — ничего не выдавать, — выдать шоколадку и рублей сдачи, — выдать шоколадку и рублей сдачи.
Например, если у человека есть одна монета номиналом в рублей и две монеты номиналом в рублей и монеты забрасываются в порядке , и рублей, то происходит следующее:
- Автомат переходит в состояние р. и ничего не выдает;
- Автомат переходит в состояние р. и ничего не выдает;
- Автомат переходит в состояние р., выдает шоколадку и не возвращает сдачу.
Способы задания автоматов
Табличный способ задания автомата Мили
Автомат Мили может быть задан таблицей переходов и таблицей выходов.
В таблице переходов АА Мили на пересечении столбца и строки записывается состояние , которое есть функция от и
В таблице выходов на пересечении столбца и строки записывается выходной сигнал, который есть функция от и .
Пример: Задание автомата Мили табличным способом (автомат имеет два входных сигнала, два выходных сигнала и три состояния).
|
Таблица переходов
|
Таблица выходов
|
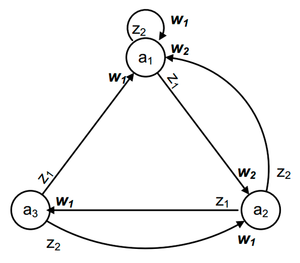
Графический способ задания автомата Мили
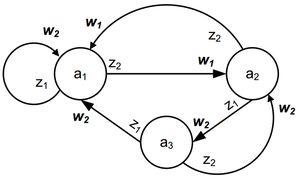
На рисунке приведен граф автомата Мили на 3 состояния, имеющий 2 входных сигнала и 2 выходных сигнала (см. предыдущий пример).
Табличный способ задания автомата Мура
В автомате Мура выходной сигнал зависит только от состояния автомата и не зависит от входного сигнала.
Поэтому достаточно для задания автомата Мура в таблице переходов добавить одну строку.
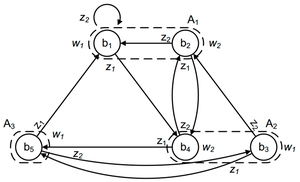
Графический способ задания автомата Мура
На рисунке приведен граф автомата Мура на 5 состояний, имеющий 2 входных сигнала и 2 выходных сигнала.
Реакция автоматов на входное слово
Автомат Мили
Допустим, входное слово поступает на вход автомата буква за буквой.
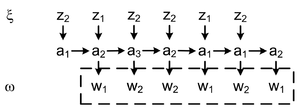
Выходное слово называется реакцией автомата Мили на входное слово в состоянии строится по таблице переходов и выходов).
Реакцию автомата на входное слово можно заменить обходом графа.
Автомат Мура
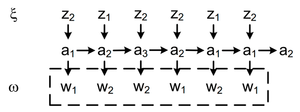
Выходное слово называется реакцией автомата Мура на входное слово в состоянии .
В рассматриваемом примере для автоматов Мили и Мура реакции автоматов на одинаковое входное слово совпадают, но они сдвинуты на один такт. Автоматы Мили и Мура дающие одинаковые реакции на одинаковые входные слова называются эквивалентными. Данное замечание приводит к задаче построения эквивалентных автоматов, дающих одинаковые реакции на одинаковые входные слова.
Эквивалентность автоматов Мили и Мура
Автомат Мура переходит в автомат Мили, если всем переходам в состояние поставить выходные воздействия этого состояния. После таких преобразований получим эквивалентный автомат Мили.
Однако, чтобы преобразовать автомат Мили в автомат Мура такой алгоритм не подходит, т.к. в одно состояние могут вести разные переходы. Но можно просто добавить новых состояний, устанавливая необходимые соответствия.
Далее будет приведено формальное доказательство факта эквивалентности с явным предъявлением конструкции.
| Теорема (Эквивалентность автоматов Мура и Мили): |
Для каждого автомата Мили может быть построен эквивалентный ему автомат Мура, и обратно — для каждого автомата Мура может быть построен эквивалентный ему автомат Мили. |
| Доказательство: |
| Для доказательства опишем алгоритмы взаимной трансформации моделей Мили и Мура и покажем эквивалентность получающихся автоматов. При этом в автоматах Мура будем пренебрегать выходным сигналом , связанным с начальным состоянием. |
Переход от автомата Мура к автомату Мили
Шестикомпонентным набором с индексом А будем обозначать автомат Мура, а с индексом В — автомат Мили.
Пусть задан автомат Мура.
Требуется перейти к автомату Мили
),
у которого , , т.е. входные и выходные алфавиты совпадают.
Рассмотрим пример, в котором , , , алфавит состояний автомата Мура содержит четыре элемента.
При переходе от автомата Мура к автомату Мили алфавиты состояний также совпадают, т.е. .
Для определения соответствия между функциями переходов выходов автоматов Мура и Мили воспользуемся следующей вспомогательной таблицей.
| Мура | Мили |
| |
|
При переходе от автомата Мура к автомату Мили функции переходов также совпадают, а для определения функции выходов выходные сигналы с вершин опускается на входные дуги.
Проделав такие преобразования мы должны доказать, что получили автомат Мили, эквивалентный автомату Мура, т.е. что реакции автоматов на одинаковые входные воздействия совпадают.
При таком переходе (Мура к Мили) число состояний совпадает.
| Утверждение: |
Полученный автомат эквивалентен исходному |
|
Пусть символ поступает на вход автомата Мура , который находится в состоянии . Следовательно, перейдет в состояние и выдаст сигнал . Соответствующий автомат Мили из состояния также перейдет в состояние и выдаст тот же сигнал . Таким образом, для выходной последовательности длины 1 поведение автоматов и полностью совпадает. Далее по индукции получаем эквивалентность автоматов. |
Переход от автомата Мили к автомату Мура
Пусть задан автомат Мили .
Требуется перейти к автомату Мура
,
у которого ; , т.е. входные и выходные алфавиты совпадают.
Рассмотрим пример, в котором , , алфавит состояний автомата Мили содержит три элемента.
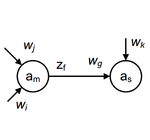
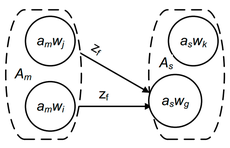
Для определения алфавита состояний, функций переходов и выходов автомата Мура воспользуемся следующей вспомогательной таблицей.
| Мура | Мили |
|
|
В данном случае .
При таком переходе (Мили к Мура) каждому состоянию автомата Мили ставится в соответствие множество всевозможных пар , где есть функция от состояния и входного сигнала, функция от состояния и входного сигнала.
Пример:
| Мура | Мили |
|
Для состояния:
В качестве начального состояния результирующего автомата может быть выбрано любое состояние Мура, порожденное начальным состоянием автомата Мили, т.е. состояния или .
При определении функции переходов результирующего автомата Мура из всех состояний, порожденных одним состоянием автомата Мили, должны быть переходы под воздействием одинаковых входных сигналов.
Поскольку в автомате Мура выходной сигнал зависит только от состояния автомата, то в примере рядом с состояниями проставим соответствующие выходные сигналы.
И так если осуществить следующие преобразования, то получим:
| Мили | Мура | Мили |
| 3 состояния | 5 состояний | 5 состояний |
Можно утверждать, что если эквивалентно , а эквивалентно , то эквивалентно (т.е. эквивалентность обладает свойством транзитивности).
| Утверждение: |
Полученный автомат эквивалентен исходному |
| Доказательство эквивалентности автоматов и аналогично предыдущему случаю. |
Методы взаимной транспозиции автоматов Мили и Мура показывают, что при переходе от автомата Мили к автомату Мура число состояний принципиально не меняется. В то время как при обратном переходе в автомат Мура число состояний, как правило, увеличивается. Вследствие транзитивности отношения эквивалентности два автомата Мили, первый из которых получен из автомата Мура, так же будут эквивалентны, но у второго автомата число состояний будет больше. Таким образом эквивалентные между собой автоматы могут иметь различное число состояний. В связи с чем и возникает задача нахождения минимального автомата в классе эквивалентных между собой автоматов. Существование для любого абстрактного автомата эквивалентного ему абстрактного автомата с минимальным числом внутренних состояний впервые было доказано Муром.
См. также
Примечания
Источники информации
- Ожиганов А.А. Теория автоматов: Учебное пособие. СПб.: НИУ ИТМО, 2013 — С. 84.
- Богаченко Н.Ф., Файзуллин Р.Т. Синтез дискретных автоматов: Учебное пособие. Омск: Издательство Наследие. Диалог-Сибирь, 2006.
- Википедия — Автомат Мура
- Ofap.ulstu.ru — Абстрактные автоматы
- Николай Борисенко — Технические аспекты построения управляющих автоматов при проектировании цифровых устройств на основе современных ПЛИС