Иерархическая кластеризация
| Определение: |
| Иерархическая кластеризация (англ. hierarchical clustering) — множество алгоритмов кластеризации, направленных на создание иерархии вложенных разбиений исходного множества объектов. |
Иерархические алгоритмы кластеризации часто называют алгоритмами таксономии. Для визуального представления результатов кластеризации используется дендрограмма — дерево, построенное по матрице мер близости между кластерами. В узлах дерева находятся подмножества объектов из обучающей выборки. При этом на каждом ярусе дерева множество объектов из всех узлов составляет исходное множество объектов. Объединение узлов между ярусами соответствует слиянию двух кластеров. При этом длина ребра соответствует расстоянию между кластерами.
Алгоритм иерархической кластеризации
Дерево строится от листьев к корню. В начальный момент времени каждый объект содержится в собственном кластере. Далее происходит итеративный процесс слияния двух ближайших кластеров до тех пор, пока все кластеры не объединятся в один или не будет найдено необходимое число кластеров. На каждом шаге необходимо уметь вычислять расстояние между кластерами и пересчитывать расстояние между новыми кластерами. Расстояние между одноэлементными кластерами определяется через расстояние между объектами: . Для вычисления расстояния между кластерами и на практике используются различные функции в зависимости от специфики задачи.
Функции расстояния между кластерами
- Метод одиночной связи (англ. single linkage)
- Метод полной связи (англ. complete linkage)
- Метод средней связи (англ. UPGMA (Unweighted Pair Group Method with Arithmetic mean))
- Центроидный метод (англ. UPGMC (Unweighted Pair Group Method with Centroid average))
- Метод Уорда (англ. Ward's method)
Формула Ланса-Уильямса
На каждом шаге необходимо уметь быстро подсчитывать расстояние от образовавшегося кластера до любого другого кластера , используя известные расстояния с предыдущих шагов. Это легко выполняется при использовании формулы, предложенной Лансом и Уильямсом в 1967 году:
, где — числовые параметры.
Каждая из указанных выше функций расстояния удовлетворяет формуле Ланса-Уильямса со следующими коэффициентами:
- Метод одиночной связи (англ. single linkage)
- Метод полной связи (англ. complete linkage)
- Метод средней связи (англ. UPGMA (Unweighted Pair Group Method with Arithmetic mean))
- Центроидный метод (англ. UPGMC (Unweighted Pair Group Method with Centroid average))
- Метод Уорда (англ. Ward's method)
Свойство монотонности
Введем обозначение — расстояние между кластерами, выбранными на шаге для объединения.
Дендрограмма позволяет представлять зависимости между множеством объектов с любым числом заданных характеристик на двумерном графике, где по одной из осей откладываются все объекты, а по другой — расстояние . Если не накладывать на это расстояние никаких ограничений, то дендрограмма будет иметь большое число самопересечений и изображение перестанет быть наглядным. Чтобы любой кластер мог быть представлен в виде непрерывного отрезка на оси объектов и ребра не пересекались, необходимо наложить ограничение монотонности на .
| Определение: |
| Функция расстояния является монотонной, если на каждом следующем шаге расстояние между кластерами не уменьшается: |
Расстояние является монотонным, если для коэффициентов в формул Ланса-Уильямса верна теорема Миллигана.
| Теорема (Миллиган, 1979): |
Если выполняются следующие три условия, то кластеризация является монотонной:
|
Из перечисленных выше расстояний теореме удовлетворяют все, кроме центроидного.
Определение числа кластеров
Для определения числа кластеров находится интервал максимальной длины . В качестве итоговых кластеров выдаются кластеры, полученные на шаге . При этом число кластеров равно .
Однако, когда число кластеров заранее неизвестно и объектов в выборке не очень много, бывает полезно изучить дендрограмму целиком.
Псевдокод
// алгоритм принимает множество объектов и возвращает множество кластеров для каждого шага function hierarchy(X: Set<Object>): Set<Set<Object>> t = 1 for i = 2 to m for in return
Пример
# Подключение библиотек from scipy.cluster.hierarchy import linkage, dendrogram from sklearn import datasets import matplotlib.pyplot as plt # Создание полотна для рисования fig = plt.figure(figsize=(15, 30)) fig.patch.set_facecolor('white') # Загрузка набора данных "Ирисы Фишера" iris = datasets.load_iris() # Реализация иерархической кластеризации при помощи функции linkage mergings = linkage(iris.data, method='ward') # Построение дендрограммы. Разными цветами выделены автоматически определенные кластеры R = dendrogram(mergings, labels=[iris.target_names[i] for i in iris.target], orientation = 'left', leaf_font_size = 12) # Отображение дендрограммы plt.show()
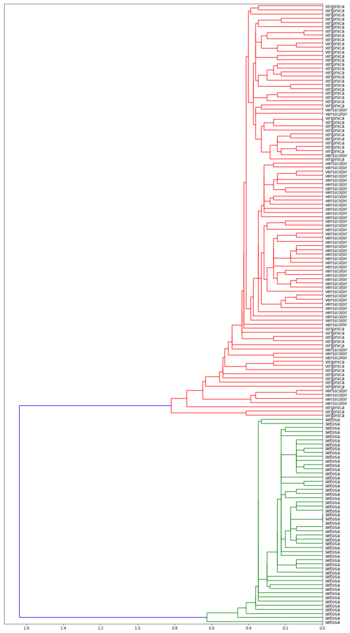
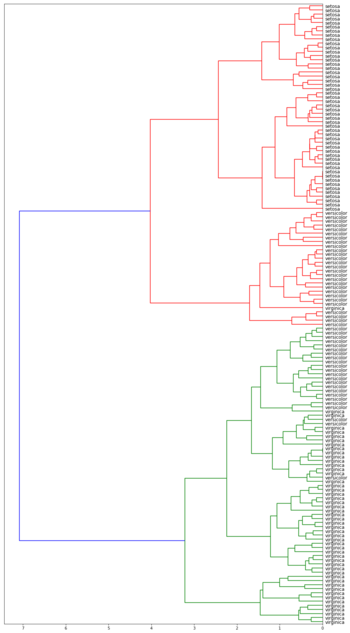
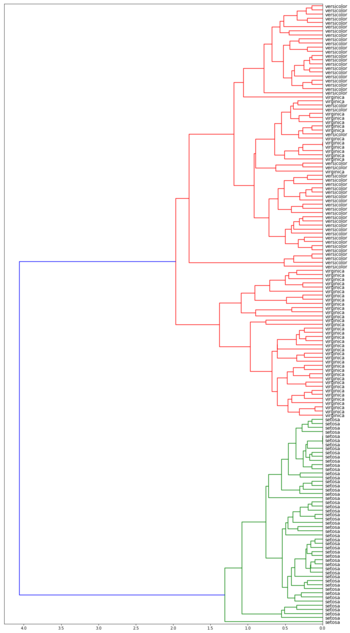
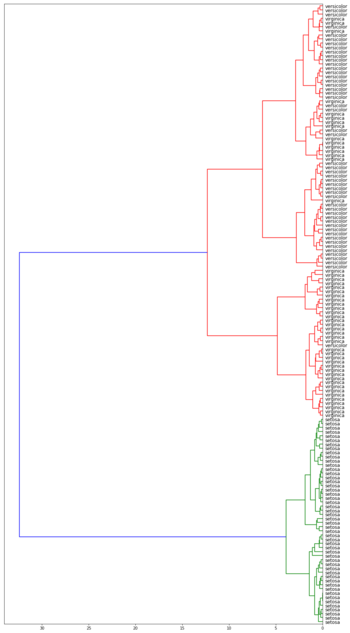
| Дендрограммы кластеризации ирисов Фишера[1] в зависимости от функции расстояния между кластерами | |||
|
| ||
| Метод одиночной связи | Метод полной связи | ||
|
| ||
| Метод средней связи | Метод Уорда | ||
Лучше всего с задачей справился алгоритм с использованием расстояния Уорда. Он точно выделил класс Iris setosa и заметно отделил вид Iris virginica от Iris versicolor.
См. также
- Кластеризация
- Оценка качества в задаче кластеризации
- EM-алгоритм
- -средних[на 28.01.18 не создан]
Примечания
Источники информации
- Википедия — Иерархическая кластеризация
- Scipy Documentation — Hierarchical clustering (scipy.cluster.hierarchy)
- К.В.Воронцов Лекции по алгоритмам кластеризации и многомерного шкалирования
- G. N. Lance, W. T. Williams; A General Theory of Classificatory Sorting Strategies: 1. Hierarchical Systems, The Computer Journal, Volume 9, Issue 4, 1 February 1967, Pages 373–380