Доказательство нерегулярности языков: лемма о разрастании

Лемма о разрастании — лемма, позволяющая во многих случаях проверить, является ли данный язык регулярным.

Лемма (о разрастании):

Пусть [math]L[/math] — регулярный язык над алфавитом [math]\Sigma[/math], тогда существует такое [math]n[/math], что для любого слова [math] \omega \in L[/math] длины не меньше [math]n[/math] найдутся слова [math] x,y,z \in \Sigma^*[/math], для которых верно: [math]xyz=\omega, y\neq \varepsilon, |xy|\leqslant n[/math] и [math]\forall k \geqslant 0~xy^{k}z\in L[/math].

Доказательство:

[math]\triangleright[/math]

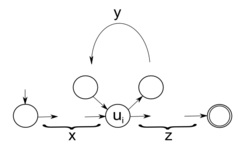
Пусть [math]L[/math] — регулярный язык над алфавитом [math]\Sigma[/math]. Поскольку регулярный язык является автоматным, то найдётся автомат [math]A[/math], допускающий язык [math]L[/math]. Пусть [math]n[/math] — размер автомата. Докажем, что [math]n[/math] удовлетворяет условию леммы. Возьмём произвольное слово [math]\omega[/math] длины не меньше [math]n[/math] из языка [math]L[/math]. Рассмотрим переходы в автомате [math]\langle s,\omega\rangle \vdash\langle u_1, \omega[0]^{-1}\omega\rangle\vdash\dots\vdash\langle u_{l},\varepsilon\rangle, \: l\geqslant n[/math]. Так как [math]l[/math] не меньше количества состояний в автомате [math]n[/math], то в переходах будет совпадение. Пусть [math]u_i[/math] и [math]u_j[/math] — первое совпадение. Тогда, повторяя участок слова [math]\omega[/math], который отвечает за переход от [math]u_i[/math] к [math]u_j[/math], получаем слово, допускаемое автоматом. То есть, если верно [math]\langle s, xyz\rangle \vdash^*\langle u_i, yz\rangle\vdash^*\langle u_j, z\rangle\vdash^*\langle u_l, \varepsilon\rangle[/math], то тогда верно [math]\langle s, xy^kz\rangle \vdash^*\langle u_i, y^kz\rangle\vdash^*\langle u_j, y^{k-1}z\rangle\vdash^*\langle u_j, z\rangle\vdash^*\langle u_l, \varepsilon\rangle[/math]. Тогда автомат [math]A[/math] допускает слово [math]xy^kz[/math], следовательно [math]xy^kz[/math] принадлежит регулярному языку [math]L[/math].

[math]\triangleleft[/math]

Замечание. Условие леммы не является достаточным для регулярности языка. (См. пример 2)

Доказательства нерегулярности языков

Для доказательства нерегулярности языка можно использовать свойства регулярных и автоматных языков.
Часто удобно использовать отрицание леммы о разрастании. Пусть [math]L[/math] — язык над алфавитом [math]\Sigma[/math]. Если для любого натурального [math]n[/math] найдётся такое слово [math]\omega[/math] из данного языка, что его длина будет не меньше [math] n[/math] и при любом разбиении на три слова [math]x,y,z[/math] такие, что [math]y[/math] непустое и длина [math]xy[/math] не больше [math]n[/math], существует такое [math]k[/math], что [math]xy^kz \notin L[/math], то язык [math]L[/math] нерегулярный.

Пример доказательства с использованием леммы

Рассмотрим язык праильных скобочных последовательностей. Для фиксированного [math]n[/math] предъявляем слово [math]\omega=(^n)^n[/math]. Пусть [math]\omega[/math] как-то разбили на [math]x, y, z[/math]. Так как [math]|xy|\leqslant n[/math], то [math]y=(^b[/math], где [math]b \gt 0[/math]. Для любого такого разбиения берём [math]k=2[/math] и получаем [math]xy^kz=(^{n+b})^n[/math], что не является правильной скобочной последовательностью. Значит, язык правильных скобочных последовательностей нерегулярен.

Пример доказательства без использования леммы

Докажем нерегулярность языка [math]0^a 1^b 2^b, a \geqslant 1, b \geqslant 0[/math]. Заметим, что здесь условие леммы о накачке выполнено [math](n = 1, x = \varepsilon, y = 0)[/math]. Докажем нерегулярность языка с помощью свойств ДКА. Пусть для языка существует автомат [math]A[/math] c [math]k[/math] состояниями. Пусть после [math]a[/math] нулей на вход поступило [math]k[/math] единиц. При помощи рассуждений, аналогичных приведенным в доказательстве леммы, получаем, что с момента завершения считывания нулей до последнего считывания единицы автомат посетит [math]k + 1[/math] состояние, т. е. хотя бы в одном из них он окажется дважды. Пусть при первом посещении этого состояния автомат считал [math]i[/math] единиц, при втором — [math]j[/math]. Поскольку [math]0^a 1^i 2^i[/math] принимается автоматом, а [math]0^a 1^j 2^i[/math] — не принимается, то при подаче автомату, находящемуся в этом состоянии, [math]i[/math] двоек, автомат, с одной стороны, должен оказаться в допускающем состоянии, с другой — в недопускающем.

См. также

• Лемма о разрастании для КС-грамматик
• Интерпретация булевых формул с кванторами как игр для двух игроков

Литература

• Хопкрофт Д., Мотвани Р., Ульман Д. — Введение в теорию автоматов, языков и вычислений, 2-е изд. : Пер. с англ. — Москва, Издательский дом «Вильямс», 2002. — 528 с. : ISBN 5-8459-0261-4 (рус.)