Шифратор и дешифратор
| Определение: |
| Дешифратор (англ. decoder) - логический элемент, получающий на вход $n$-значное число $x$ в двоичном представлении и выводящий $1$ на $x$-м выходе. На все остальные выходы выдаёт элемент выдаёт $0$. |
| Определение: |
| Шифратор (англ. encoder) - логическое устройство, которое имеет $2^n$ входов и $n$ выходов. Если подать сигнал ровно на один вход, то на выходы будут кодировать номер входа, на который подан сигнал. |
Принцип работы дешифратора
Для начала разберёмся, как работает дешифратор 2-to-4 (это значит, что у этого дешифратора есть два входа $s_0$ и $s_1$ и четыре выхода $z_0$, $z_1$, $z_2$ и $z_3$). Если $s_0 = s_1 = 0$, то на выходе $z_0$ будет значение $1$, на остальных выходах будет $0$. Если же $s_0 = 1$ и $s_1 = 0$, то на выходе $z_1$ будет $1$, на остальных выходах будут $0$. Если $s_0 = 0$ и $s _1 = 1$, то на выходе $z_2$ будет $1$, а на остальных входах будет $0$. Если же $s_0 = s_1 = 1$, то на выходе $z_3$ будет $1$, а на других - $0$. Для более лучшего понимания обратимся к таблице истинности.
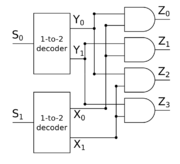
Логическая схема дешифратора
Преимущество дешифратора заключается в том, что размер схемы линейно зависит от входов. Принцип построения такой схемы заключается в том, что мы сначала строим схему для $n-1$ входов, потом пытаемся добавить $n$-ый вход так, чтобы схема оставалась корректной. Заметим, что если на $X$ подать $0$, то на всех выходах $Z_0$, $Z_1$, $\ldots$, $Z_{2^n - 1}$ будет $0$, а если подать $1$, то $1$ должна оказаться только на выходе $Z_i$, где $i$ кодируется входами $S_0$, $S_1$, $\ldots$, $S_{n-1}$. Давайте построим такую схему, чтобы с помощью гейтов $NOT$ и $AND$ у нас получилось ровно $2^n$ различных вариантов значений на входах $S_0$, $S_1$, $\ldots$, $S_{n-1}$.