List order maintenance
List order maintance — проблема поддержки списка со следующими командами:
- — вставка нового элемента в список сразу после ;
- — удаление элемента из списка;
- — команда, возвращающая , если в списке находится до и иначе.
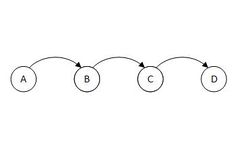
Структура данных подходит и для односвязных, и для двусвязных списков.
Алгоритм
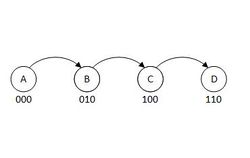
Рассмотрим реализацию списка с командой порядка, где все операции выполняются за амортизационную . Дадим каждому элементу списка метки длины из битов. Пусть , где - количество элементов в списке. Если после добавления или удаления элементов перестанет удовлетворять неравенству, пересчитаем все метки заново. Пересчет меток занимает амортизационно по аналогии с саморасширяющимся массивом. Пусть метки идут по возрастанию от начала к концу списка, тогда операцию можно сделать, сравнив метки за . Теперь опишем взаимодействие с метками при выполнении других команд.
Для выполнения просто удалим элемент вместе с его меткой, проверим, удовлетворяет ли неравенству, если нет - пересчитаем. Для существуют два возможных случая:
Метка : , где — следующий за элемент в списке. Тогда между метками и есть свободная метка, которую мы дадим . После этого опять проверим на соответствие неравенству.
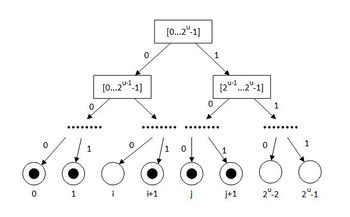
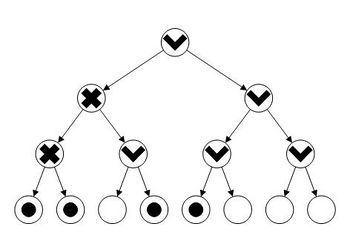
В случае, если между метками и свободной метки нет, нам придется пересчитать метки следующим образом. Построим виртуальное дерево отрезков над всеми возможными метками, где в каждом узле будем хранить бит. В листьях будем хранить, используется ли уже эта метка. Пусть — это количество помеченных (используемых) листьев (меток) в поддереве , а — это количество всех листьев в поддереве . Для любой будем считать, что узел дерева переполнен, если . Именно наличие переполненности мы и будем хранить во всех нелистовых узлах. Стоит заметить, что все листья всегда непереполнены. В худшем случае: . Получается, что чем выше, тем более разреженными должны быть поддеревья непереполненных узлов.
Тогда, как только мы получаем команду вставить элемент элемент, которому не хватает метки, мы поднимаемся вверх от метки элемента , пока не найдем первый непереполненный узел. Может случиться такое, что на всем пути до корня мы не найдем ни одного непереполненного узла. Чтобы этого избежать, изменим требования к позже. Как только мы нашли первый непереполненный узел, переназначим метки в его поддереве так, чтобы они находились друг от друга на одинаковых расстояниях (места точно хватит, так как , если узел непереполненный). После этого плотность распределения всех занятых листьев составит примерно .
Тогда чтобы после перераспределения меток в поддереве узла , мы заново пришли к этому же узлу за перераспределением, нужно, чтобы его сын снова переполнился. Если — сын , то он переполнится, когда . Чтобы это произошло, требуется, чтобы было сделано еще добавлений.