XOR-SAT

Задача:

[math]\mathrm {XORSAT}[/math] (XOR-satisfiability) выполнимость функции — задача распределения аргументов в булевой КНФ функции, записанной в виде XOR-КНФ, таким образом, чтобы результат данной функции был равен [math] 1 [/math].

Описание

Одним из особых случаев [math]\mathrm {SAT}[/math] является класс задач, где каждый конъюнкт содержит операции [math]\oplus[/math] (т. е. исключающее или), а не (обычные) [math]\lor[/math] операторы.Формально, обобщенная КНФ с тернарным булевым оператором [math] R[/math] работает только если [math] 1[/math] или [math] 3[/math] переменные дают [math] \mathtt {true}[/math] в своих аргументах. Конъюнкты, имеющие более [math] 3[/math] переменных могут быть преобразованы в сочетании с формулой преобразования с сохранением выполнимости булевой функции, т. е. [math]\mathrm {XOR}[/math]-[math]\mathrm {SAT}[/math] может быть снижена до [math]\mathrm {XOR}[/math]-[math]3[/math]-[math]\mathrm {SAT}[/math]

Это задача [math]\mathrm {P}[/math]-класса, так как [math]\mathrm {XOR}[/math]-[math]\mathrm {SAT}[/math] формулу можно рассматривать как систему линейных уравнений по модулю [math]2[/math], которая, в свою очередь, может быть решена за [math]O(n^3)[/math] методом Гаусса .Такое представление возможно на основе связи между Булевой алгеброй и Булевым кольцом и том факте, что арифметика по модулю [math]2[/math] образует конечное поле .

Пример решения XORSAT

Пример

Красные пункты могут быть добавлены для возможности представления КНФ-функции в виде [math]\mathrm {XOR}[/math]-[math]\mathrm {SAT}[/math].

[math](a \oplus b \oplus c) \land (b \oplus \neg c \oplus d) \land (a \oplus b \oplus \neg d) \land (a \oplus \neg b \oplus \neg c)[/math]	[math] \land (\neg a \oplus b \oplus c) [/math]

Решение XOR-SAT задачи методом Гаусса
Система уравнений Переменные Значение [math] a [/math] [math]\oplus[/math] [math] c [/math] [math]\oplus[/math] [math] d [/math] [math]=1[/math] [math] b [/math] [math]\oplus[/math] [math]\neg c [/math] [math]\oplus[/math] [math] d [/math] [math]=1[/math] [math] a [/math] [math]\oplus[/math] [math] b [/math] [math]\oplus[/math] [math]\neg d [/math] [math]=1[/math] [math] \neg a [/math] [math]\oplus[/math] [math] \neg b [/math] [math]\oplus[/math] [math]\neg c [/math] [math]=1[/math] [math] \neg a [/math] [math]\oplus[/math] [math] b [/math] [math]\oplus[/math] [math] c [/math] [math] =1 [/math]	(«[math]1[/math]» означает «[math] \mathtt {true}[/math]», «[math]0[/math]» означает «[math] \mathtt {false}[/math]») Каждый конъюнкт ведет к одному уравнению.
Нормированная система уравнений Переменные Значение [math] a [/math] [math]\oplus[/math] [math] c [/math] [math]\oplus[/math] [math] d [/math] [math]=1[/math] [math] b [/math] [math]\oplus[/math] [math] c [/math] [math]\oplus[/math] [math] d [/math] [math]=0[/math] [math] a [/math] [math]\oplus[/math] [math] b [/math] [math]\oplus[/math] [math] d [/math] [math]=0[/math] [math] a [/math] [math]\oplus[/math] [math] b [/math] [math]\oplus[/math] [math] c [/math] [math]=1[/math] [math] a [/math] [math]\oplus[/math] [math] b [/math] [math]\oplus[/math] [math] c [/math] [math] =0 [/math]	Используя свойства Булевых колец ([math]\neg x=1 \oplus x[/math], [math]x \oplus x=1[/math]), избавимся от отрицаний в нашей системе
Матрица соответствующих коэффициентов [math]a[/math] [math]b[/math] [math]c[/math] [math]d[/math] Строка [math]1[/math] [math]0[/math] [math]1[/math] [math]1[/math] [math]1[/math] [math]A[/math] [math]0[/math] [math]1[/math] [math]1[/math] [math]1[/math] [math]0[/math] [math]B[/math] [math]1[/math] [math]1[/math] [math]0[/math] [math]1[/math] [math]0[/math] [math]C[/math] [math]1[/math] [math]1[/math] [math]1[/math] [math]0[/math] [math]1[/math] [math]D[/math]	Составим матрицу по следующему правилу: Если переменная присутствовала в данном конъюнкте ставим в ячейку [math]1[/math], иначе [math]0[/math]
Преобразования, чтобы сформировать верхнюю треугольную матрицу [math]a[/math] [math]b[/math] [math]c[/math] [math]d[/math] Операция [math]1[/math] [math]0[/math] [math]1[/math] [math]1[/math] [math]1[/math] [math]A[/math] [math]1[/math] [math]1[/math] [math]0[/math] [math]1[/math] [math]0[/math] [math]C[/math] [math]1[/math] [math]1[/math] [math]1[/math] [math]0[/math] [math]1[/math] [math]D[/math] [math]0[/math] [math]1[/math] [math]1[/math] [math]1[/math] [math]0[/math] [math]B[/math]	Поменяем местами строки [math]B,\ C,\ D[/math], чтобы упростить получение верхней треугольной матрицы.
[math]1[/math] [math]0[/math] [math]1[/math] [math]1[/math] [math]1[/math] [math]A[/math] [math]0[/math] [math]1[/math] [math]1[/math] [math]0[/math] [math]1[/math] [math]E=C \oplus A[/math] [math]0[/math] [math]1[/math] [math]0[/math] [math]1[/math] [math]0[/math] [math]F=D \oplus A[/math] [math]0[/math] [math]1[/math] [math]1[/math] [math]1[/math] [math]0[/math] [math]B[/math]	Т.к. операция [math]\oplus[/math] даёт [math]0[/math] при одинаковых аргументах, применим её для строк [math]A,\ C=E[/math] и [math]A,\ D=F[/math], чтобы получить [math]0[/math] в [math]1[/math]-м столбце.
[math]1[/math] [math]0[/math] [math]1[/math] [math]1[/math] [math]1[/math] [math]A[/math] [math]0[/math] [math]1[/math] [math]1[/math] [math]0[/math] [math]1[/math] [math]E[/math] [math]0[/math] [math]0[/math] [math]1[/math] [math]1[/math] [math]1[/math] [math]G=F \oplus E[/math] [math]0[/math] [math]0[/math] [math]0[/math] [math]1[/math] [math]1[/math] [math]H=B \oplus E[/math]	Теперь применим [math]\oplus[/math] для строк [math]E,\ F=G[/math] и [math]B,\ E=H[/math], чтобы получить [math]0[/math] в [math]2[/math]-м и [math]3[/math]-м столбцах.
Преобразования, чтобы сформировать диагональную матрицу [math]a[/math] [math]b[/math] [math]c[/math] [math]d[/math] Операция [math]1[/math] [math]0[/math] [math]1[/math] [math]0[/math] [math]0[/math] [math]I=A \oplus H[/math] [math]0[/math] [math]1[/math] [math]1[/math] [math]0[/math] [math]1[/math] [math]E[/math] [math]0[/math] [math]0[/math] [math]1[/math] [math]0[/math] [math]0[/math] [math]J=G \oplus H[/math] [math]0[/math] [math]0[/math] [math]0[/math] [math]1[/math] [math]1[/math] [math]H[/math]	Чтобы получить основную диагональную матрицу, сделаем [math]\oplus[/math] [math]A,\ H=I[/math] и [math]G,\ H=J[/math], чтобы получить [math]0[/math] в [math]4[/math]-м столбце выше диагонали.
[math]1[/math] [math]0[/math] [math]0[/math] [math]0[/math] [math]0[/math] [math]K=I \oplus J[/math] [math]0[/math] [math]1[/math] [math]0[/math] [math]0[/math] [math]1[/math] [math]L=E \oplus J[/math] [math]0[/math] [math]0[/math] [math]1[/math] [math]0[/math] [math]0[/math] [math]J[/math] [math]0[/math] [math]0[/math] [math]0[/math] [math]1[/math] [math]1[/math] [math]H[/math]	Осталось сделать [math]\oplus[/math] [math]I,\ J=K[/math] и [math]E,\ J=L[/math], потому что они отличаются в [math]1[/math]-м и [math]2[/math]-м столбцах.

Решение

Если красный пункт присутствует: Решений нет
Иначе:
[math]a=0=\mathtt {false}[/math]
[math]b=1=\mathtt {true}[/math]
[math]c=0=\mathtt {false}[/math]
[math]d=1=\mathtt {true}[/math]

Вычислительная сложность

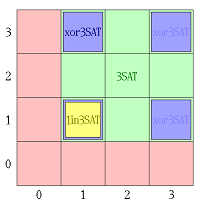
Формула с [math]2[/math]-мя дизъюнктами может быть неудовлетворена(красный), [math]3[/math]-[math]\mathrm {SAT}[/math](зелёный), [math]\mathrm {XOR}[/math]-[math]3[/math]-[math]\mathrm {SAT}[/math](синий), или/и [math]1[/math]-[math]\mathrm {in}[/math]-[math]3[/math]-[math]\mathrm {SAT}[/math], в зависимости от количества переменных со значением [math] \mathtt {true}[/math] в [math]1[/math]-м (горизонтальном) и втором (вертикальном) конъюнкте.

Поскольку [math]a \oplus b \oplus c[/math] принимает значение [math] \mathtt {true}[/math], если и только если [math]1[/math] из [math]3[/math] переменных [math]\{a,\ b,\ c\}[/math] принимает значение [math] \mathtt {true}[/math], каждое решение в [math]1[/math]-[math]\mathrm {in}[/math]-[math]3[/math]-[math]\mathrm {SAT}[/math] задачи для данной КНФ-формулы является также решением [math]\mathrm {XOR}[/math]-[math]3[/math]-[math]\mathrm {SAT}[/math] задачи, и, в свою очередь, обратное также верно.
Как следствие, для каждой КНФ-формулы, можно решить [math]\mathrm {XOR}[/math]-[math]3[/math]-[math]\mathrm {SAT}[/math]-задачу и на основании результатов сделать вывод, что либо [math]3[/math]-[math]\mathrm {SAT}[/math] задача решаема или, что [math]1[/math]-[math]\mathrm {in}[/math]-[math]3[/math]-[math]\mathrm {SAT}[/math]-задача нерешаема.
При условии, что [math]\mathrm {P}[/math]- и [math]\mathrm {NP}[/math]-классы не равны, ни [math]2[/math]-, ни Хорн-, ни [math]\mathrm {XOR}[/math]-[math]\mathrm {SAT}[/math] не являются задачи [math]\mathrm {NP}[/math]-класса, в отличии от [math]\mathrm {SAT}[/math].

См. также

• Специальные формы КНФ
• 2SAT
• NP-полнота задачи о выполнимости булевой формулы в форме 3-КНФ

Источники информации

• Википедия — Boolean satisfiability problem
• Cook, Stephen A.Proceedings of the 3rd Annual ACM Symposium on Theory of Computing: 151–158, 1971.