Матрица Кирхгофа
| НЕТ ВОЙНЕ |
|
24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян. Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием. Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей. Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить. Антивоенный комитет России |
| Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению. |
| meduza.io, Популярная политика, Новая газета, zona.media, Майкл Наки. |
| Определение: |
| Матрицей Кирхгофа простого графа называется матрица , элементы которой определяются равенством: |
Иными словами, на главной диагонали матрицы Кирхгофа находятся степени вершин, а на пересечении -й строки и -го столбца () стоит , если вершины с номерами и смежны, и в противном случае.
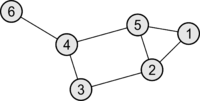
Пример матрицы Кирхгофа
Некоторые свойства
| Утверждение: |
Сумма элементов каждой строки (столбца) матрицы Кирхгофа равна нулю:
|
| Утверждение: |
Определитель матрицы Кирхгофа равен нулю:
|
|
Прибавим к первой строке все остальные строки (это не изменит значение определителя):
Так как сумма элементов каждого столбца равна , получим: |
| Утверждение: |
Матрица Кирхгофа простого графа симметрична:
|
| Утверждение: |
Связь с матрицей смежности:
|
| Утверждение: |
Связь с матрицей инцидентности:
|
| Утверждение: |
является собственным значением матрицы, кратность его равна числу компонент связности графа. |
|
Собственным значением матрицы называют значения , которые удовлетворяют уравнению:
Прибавим к первой строке все остальные строки (это не изменит значение определителя):
Так как сумма элементов каждого столбца равна , получим:
Следовательно, является собственным значением. Доказательство кратности: Пусть дан граф c компонентами связности. Перенумеруем его вершины так, чтобы сначала шли вершины первой компоненты связности, затем второй и т.д. Тогда матрица Кирхгофа примет блочно-диагональный вид, и -тый блок этой матрицы будет являтся матрицей Кирхгофа для -той компоненты связности. Из свойства блочно-диагональной матрицы , где — матрица Кирхгофа для -той компоненты связности, и свойства, доказанного выше, |
См. также
Источники информации
- Асанов М., Баранский В., Расин В.: Дискретная математика: Графы, матроиды, алгоритмы. стр. 18
- Википедия — Матрица Кирхгофа